基于模糊AHP的卫星导航定位能力综合评估模型
2012-12-15时零许瑞明
时零,许瑞明
(1.北京环球信息应用开发中心,北京100194;2.军事科学院 军事运筹分析研究所,北京100091)
1 导航定位能力指标体系
导航定位能力主要由定位精度和精确测速能力组成。
1.1 定位精度
导航定位精度除了理论值的计算,还受定位误差的影响。误差来源主要有4个方面[1]:①卫星部分:卫星星历误差、卫星钟差;②用户接收机部分:用户接收机测量误差、通道偏差;③信号传播路径:电离层的信号传播延迟、对流层的信号传播延迟、多路径效应;④其他影响:相对论效应、地球自转影响。其中,接收机测量噪声和通道偏差大小与接收机的设计有关,属于内部误差;其他误差受外界因素影响,与接收机无关,相对于接收机而言属于外部误差。
(1)定位精度理论值:对于像GPS这样的卫星导航系统,用户的定位测量方程见参考文献[2]。
(2)卫星部分的误差:卫星钟差,卫星上采用高精度原子钟,用户定位时通常认为每颗卫星之间的星上时钟是精密同步的,但实际上卫星时间并非系统时间,且每颗卫星的时钟也都存在小的差异;轨道误差,轨道误差一般是指根据广播星历或者后处理星历求得的卫星轨道与真实轨道之间的不符值;相对论效应,由于地球自转运动和卫星轨道高度的变化,以及地球重力场的变化,相对论效应的影响并不是常数,经过改正后仍有残余影响。
(3)用户接收机部分的误差:地球自转参数是地球定向参数的一部分,它是实现天球参考架与地球参考架互相转换的参数,精密定轨和导航都需要高精度的地球自转参数,因此它的误差研究具有重要的意义;固体潮的存在使地面有周期性的变形以及地面点的垂线产生偏移,也使测站的瞬时天文经纬度受到不同的影响,进而影响定位精度的准确性;一般把每个观测瞬间的接收机钟差作为独立未知数,列入观测方程中与测站坐标向量一并求解。这一动态过程的误差可以等于接收机测距噪声,通常按照随机误差处理。
(4)信号传播路径误差:信号传播延迟是卫星导航系统中一项非常重要的误差源,是影响系统定位精度的关键因素之一。如何建立精确的电离层、对流层延迟以及多路径效应误差模型,真实地反映用户接收机受传播延迟的影响情况,是系统误差分析的难题之一。在作误差分析时,通常将此项误差作随机误差处理,且关于每颗卫星的伪距测量误差大小相同。

图1 卫星导航定位能力评估指标体系
1.2 精确测速能力
考虑不同的信号载荷(如:军码信号、民码信号或其他信号等)以及不同的频点组合,卫星导航系统定位应用有多种模式,则相应的测速应用也有多种模式。总体来说,精确测速包括单频测速和双频测速[3],每个方面又分不同的频点为主用模式,其他频点相应的单频测速为辅用模式。精确测速能力需全面掌握导航系统各个频点信号的测速功能和性能,便于不同频点间观测数据和测速结果的比较分析。
1.3 导航定位能力评估指标体系
结合卫星导航定位能力评估需求,建立的卫星导航定位能力评估指标体系如图1所示。
2 基于模糊理论的指标量化方法
人们对指标的评价往往采用是否达到满意来描述如最满意、较满意、最不满意等,即用满意度等级来反映人们对指标的满意程度。由于对单项指标无法直接进行满意度的统一定量计算,因此只能根据领域专家给出有关满意度的定性判断,然后借助模糊处理方法得出各项指标的模糊满意度,从而进一步得到各项指标的模糊向量。
2.1 定量指标的模糊向量
在卫星导航定位能力评估指标体系中,定位精度属于定量指标,采用以下方法进行模糊向量计算:设模糊满意度级别数为N,用X1,X2,…,XN分别表示满意度从高到低的级别,并由领域专家根据单项指标的数据变化范围,给出与各满意度级别相应的模糊隶属函数。
定位精度值及各种误差均属于越小越好型指标,设满意度级别有五个,分别为“最高、较高、中等、较低、最低”。在实际应用中,定位精度理论值可根据定位测量方程计算[2],星上误差、接收机误差和传播路径误差可通过多次测量获得,而对于这三个和误差相关的指标,又分别由多种具体误差因素所组成,如卫星钟差,可根据公式(1)建立其隶属度函数。
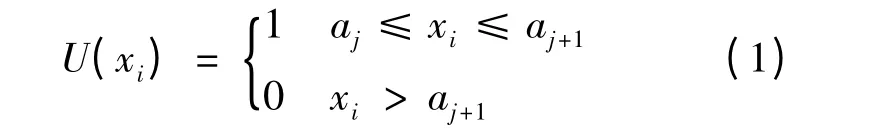
式(1)中,xi(i=1,2,3)为实测值,aj(j=1,2,…,5)为满意度级别对应的距离偏差范围。按照上述方法,可建立其它指标的隶属度函数,并计算各指标的模糊向量。参考文献[4]给出了GPS系统定位误差因素及对应等效距离偏差。
2.2 定性指标的模糊向量
在卫星导航定位能力评估指标体系中,精确测速能力属于定性指标。对于定性指标,由于其本身的复杂性,不能用精确的数学表达式表示,也很难用具体的模糊分布来确定其隶属度。因此采用专家评价法来确定定性指标的模糊向量,其基本方法如下:设评价集V={V1,V2,…,Vn},Vj(j=1,2,…,n)表示由高到低的评语。精确测速能力就用“很好、较好、一般、较差、很差”来表示。每位专家根据该系统的实际情况针对某个指标给出具体的评价,设n为有效咨询次数,yij为指标i被评为Vj的次数,则有Rj=,归一化处理后得该指标模糊向量为R=(R1,R2,…,Rn)。
3 基于AHP的模糊综合评估模型
在卫星导航定位能力评估中,各评估指标对整体能力评估的影响程度不尽相同,可用层次分析法来确定各指标权重。根据卫星导航定位能力评估的实际,建立模糊综合评估模型。
3.1 划分子因素集
用U代表卫星导航定位能力,将其按照某种属性,分成s个子集,记为{U1,U2,…,Us},并满足条件:
①U1∨U2∨…∨Us=U;②对任意的i=j,有Ui∧Uj=Ø。
设第i个子集的因素为Ui,应满足条件Ui={Ui1,Ui2,…,Uin}(i=1,2,…,s),式中ni表示Ui中的元素个数,且满足n1+n2+…+ns=n,n表示U的元素个数。
其中U={U1,U2},U1和U2分别代表定位精度和精确测速能力,则U1下属4个指标定位精度理论值、卫星误差、接收机误差、传播路径误差分别表示为U1={U11,U12,U13,U14},U2下属2个指标单频测速能力和双频测速能力分别表示为U2={U21,U22}。
3.2 子因素集Ui单因素综合评价
设评价集为W={w1,w2,…,wm},Ui中各因素Uini相对于Ui的权重分配为Wi={wi1,wi2,…,wini},且满足=1。若Ri为Ui到W的模糊评价矩阵,Ri=(rij,k)ni×m(i=1,2,…,s;j=1,2,…,n;k=1,2,…,m);式中rij,k表示因素Uij被评为wk的模糊隶属度。则得到每一级的综合评价向量为Bi=Ai·Ri=(bi1,bi2,…,bim)(i=1,2,…,s),这里的模糊算子采用乘法算子[6]。
根据定位测量方程[2]计算出运用某卫星导航系统定位后的点位坐标,与该点已知坐标位置相比较计算后,得出定位精度理论值为24m。其余误差满意度参数aj(j=1,2,…,5)由专家给出,见表1。
对各指标参数作1000次测量,根据公式(1)可计算出其隶属度,归一化处理后得到U11、U12、U13、U14对应评价矩阵R1、R2、R3、R4,进而得到该一级的综合评价向量B1、B2、B3、B4。

表1 各指标实际测量值满意度参数
3.3 因素U二级综合评价
将每个Ui视为U的一个因素,Bi作为它的单因素评价向量,可构成U到W的模糊评价矩阵[7]:
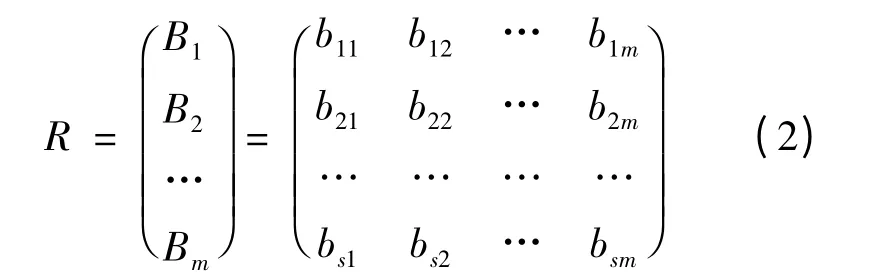
以U11到U14为元素,用B1到B4构造因素评价矩阵;每个Ui作为U的一部分,其权重向量为A=(a1,a2,…,as),则二级综合评价向量为B=A·R=(b1,b2,…,bs)。
由于U11到U14、U21和U22仍属于U1、U2的一部分,则以U1到U2为元素,用对应的B5和B6构造因素评价矩阵,则运用上述综合评价方法再进行一次三级综合评价,得出导航定位能力U的模糊综合评价。
4 实际算例
为获取某一卫星导航系统原始数据,请教一批该领域专家,发放调查问卷若干,在问卷中有以下几个方面的问题:关于卫星导航定位能力评估指标的相对重要性;对于一些定量指标,确定相关特性参数值;对于一些定性指标,根据指定评语集给出相关评语。
根据各专家给出的对评估指标中相对重要性的数据,按照AHP计算得各指标的权重向量为:A=(0.678,0.322);A1=(0.287,0.219,0.35,0.144);A2=(0.476,0.524);A3=(0.098,0.206,0.696);A4=(0.107,0.533,0.360);A5=(0.820,0.016,0.164)。
其中,A为第二层指标相对第一层指标权重向量,A1、A2分别为定位精度、精确测速能力下层指标权重向量,A3、A4、A5分别为卫星误差、接收机误差和传播路径误差下层指标权重向量。
由于定位精度理论值是一个计算得出的确定值,则评价矩阵为:R1=(1 0 0 0),R2到R4的评价矩阵分别是:

根据上述模型可得出:
B1=(1,0,0,0),B2=(0.210,0.739,0.051,0,0),B3=(0.175,0.736,0.089,0,0),B4=(0.117,0.785,0.098,0,0)
单频测速能力的模糊向量:有182位专家认为“很好”,228位专家认为“较好”,45位专家认为“一般”,没有专家认为“较差”和“很差”,归一化处理后得到单频测速能力的模糊向量R5=(0.4,0.5,0.1,0,0),同理得出双频测速能力的模糊向量R6=(0.3,0.6,0.1,0,0),则定位精度综合评价向量B5=(0.284,0.648,0.068,0,0,),精确测速能力综合评价向量B6=(0.348,0.552,0.1,0,0)。
1 王莉.卫星导航系统定位精度估计[J].飞行器测控学报,2008,27(2):81-83.
2 许其凤.区域卫星导航系统的卫星星座[J].测绘工程,2001,10(1);1-5.
3 谭述森.卫星导航定位工程(第2版)[M].北京:国防工业出版社,2010.
4 周文宏.影响GPS定位精度的因素及改进方法[J].安徽科技,2009,(9):50.
5 ZADEH L A.Fuzzy Sets[J].Information and Control,1965,(8):338-353.
6 方述诚,王定伟.模糊数学与模糊优化[M].北京:科学出版社,1997.
7 李洪兴,汪群,段钦治,等.工程模糊数学方法及应用[M].天津:天津科学技术出版社,1993.
