Cesaro函数空间CESp 的依测度收敛的Opial性质和强端点

于非非，李 君

(天津科技大学理学院，天津 300457)

Opial于 1967年[1]引入了 Opial性质的概念，这一性质蕴含不动点性质，这样的 Opial性质为序列空间所独有.1996年王廷辅等[2]讨论了 Orlicz序列空间的 Opial性质.对于函数空间，作者在文献[3]中引入了函数空间中的新概念——依测度收敛的 Opial性质，并且讨论了 Orlicz函数空间LM中依测度收敛的Opial性质的等价叙述，给出了LM中依测度收敛的Opial模的计算公式.

Cesaro函数空间CESp是全体定义在(0,+∞)并具有有限范数

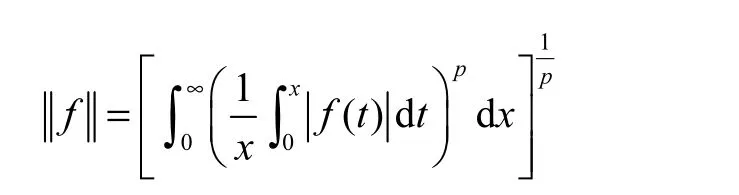
的可测函数 f(x)所构成的空间，其中1＜p＜∞．对于该空间的性质讨论并不多，1987年 Polly等[4]论证了CESp是可分的Banach空间，在等价范数意义下讨论了共轭空间；2003年刘郁强[5]用矢值序列空间的方法研究了 Cesaro函数空间的几何性质，其中就论证了Cesaro函数空间严格凸但非一致凸；2008年Astashkin 等[6]证明了CESp不具有不动点性质，2011年[7]又讨论了CESp的同构问题．

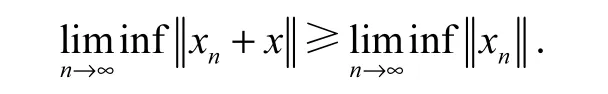
不影响讨论结果的情况下简记为

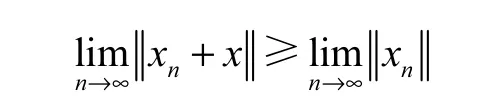
定义2 x∈S(X )称为B(X)的强端点，如果{xn}⊂X,{yn}⊂X ，xn+yn=2x(n=1,2,3?)，→1，→ 1，蕴含→ 0(n→ ∞)．

定义3 如果S(X)中的任一点均为B(X)的强端点，则X是中点局部一致凸的.

本文论证了CESp在上述范数意义下具有依测度收敛的 Opial性质；证明了∀z∈S (CESp)都是B(CESp)的强端点，进而证明了CESp(0＜p＜∞)是中点局部一致凸的．这样的论证对于该函数空间几何性质、点态性质的完善具有重要意义．有关 Banach空间的几何理论及常见记号见参考文献[8]

定理1 Cesaro函数空间CESp(1＜p＜∞)具有依测度收敛的Opial性质.

于是容易得到

所以在区间(0,a)有

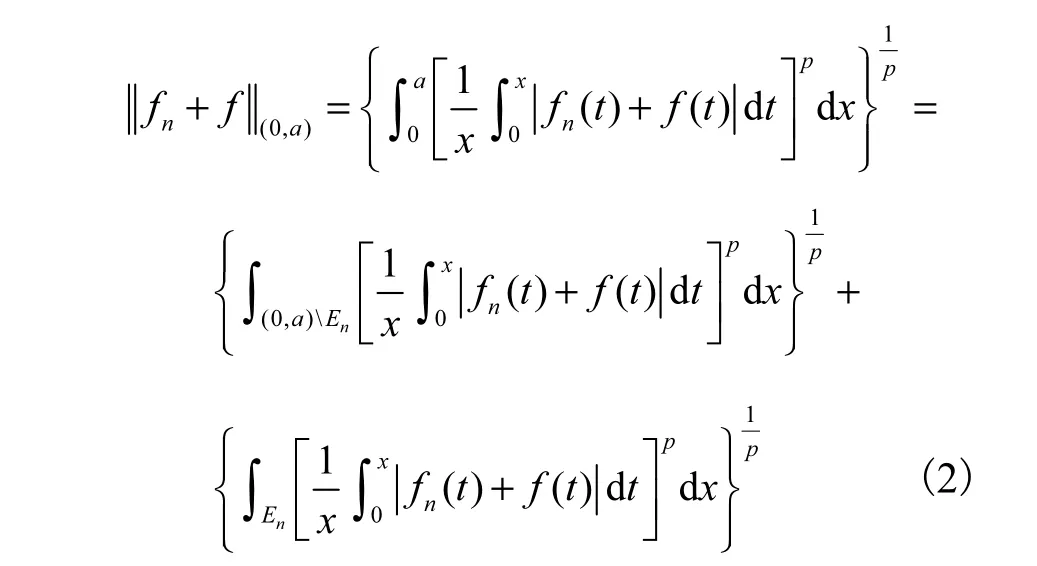
由空间理论知识及式(1)知

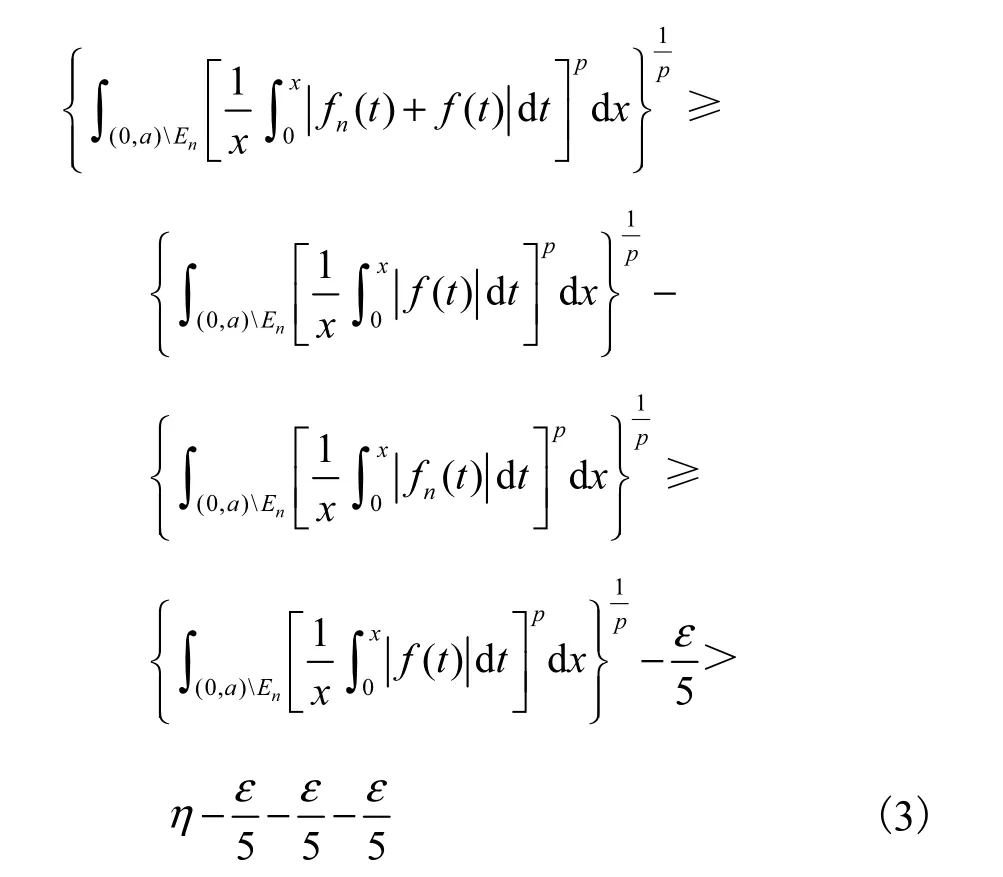
而n充分大时，总有

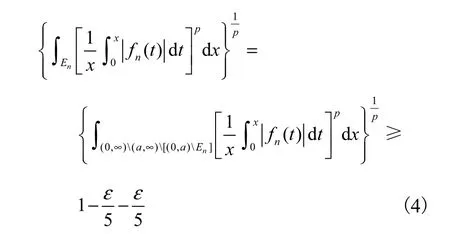
结合式(2)—(4)有

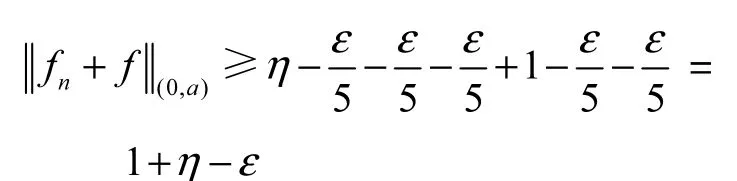
所以

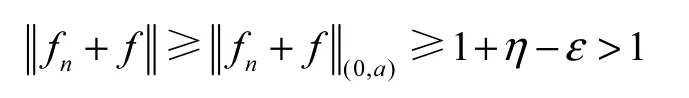
这也就证明了

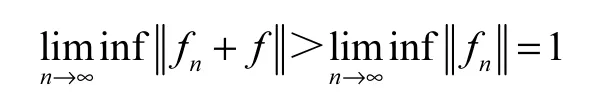
即CESp(1＜p ＜∞)具有依测度收敛的Opial性质.

定理2 ∀z∈S (CESp)都是B(CESp)的强端点.

这样就证明了∀z∈S (CESp)都是B(CESp)的强端点.

推论 Cesaro函数空间CESp(1＜p＜∞)是中点局部一致凸的.

关于函数空间CESp(1＜p＜∞)的其他点态性质、几何性质及各种几何常数的讨论，有待于大量研究工作予以完善.

［1］ Opial Z. Weak convergence of the sequence of successive approximations for nonexpansive mappings[J]. Bulletin of the American Mathematical Society，1967，73(4)：591–597.

［2］ 王廷辅，崔云安. Orlicz序列空间的 Opial性质[J]. 应用数学，1996，9(3)：392–394.

［3］ 于非非，崔云安. Orlicz函数空间的依测度收敛的Opial性质[J]. 黑龙江大学自然科学学报，2002，19(1)：6–9.

［4］ Polly Wee Sy，Zhang Wenyao，Lee Peng Yee. The dual of Cesaro function spaces [J]. Glasnik Matematicki，1987，22(42)：103–112.

［5］ 刘郁强. Cesaro函数空间的几何性质[J]. 华南师范大学学报：自然科学版，2003(4)：1–4.

［6］ Astashkin S V，Maligranda L. Cesaro function spaces fail the fixed point property [J]. Proceedings of the American Mathematical Society，2008，136(12)：4289–4294.

［7］ Astashkin S V，Maligranda L. Geometry of Cesaro function spaces [J]. Functional Analysis and Its Applications， 2011，45(1)：64–68.

［8］ 俞鑫泰. Banach空间几何理论[M]. 上海：华东师范大学出版社，1985：213–301.