基于贪心算法和遗传算法的仓储车辆调度算法

王友钊，彭宇翔，潘芬兰

(浙江大学仪器科学与工程学系，浙江杭州310027)

0 引言

随着现代物流技术的发展，自动化仓储系统在生产和流通领域得到了越来越广泛的应用。自动化仓储系统的管理技术，特别是调度技术日益成为自动化仓储系统的关键技术之一。一般任务调度算法有2种:一种是累积一定任务后的统一调度，称为静态调度;另一种是调度安排随着新任务的进入而改变，称为动态调度。本文提出的算法主要解决大型仓库中运输车辆的静态任务调度问题。

任务调度的目标是把任务分配到各被调车辆上，安排车辆的执行次序，使其在满足约束前提下完成时间最短。任务调度问题是经典的NP-Hard问题，为解决这一问题许多学者提出了多种启发式调度算法，例如:模拟退火算法、蚁群调度算法、BDCP 调度法等［1，2］。遗传算法(genetic algorithm，GA)因其可比其他调度算法获得更好的解，而被应用得最多的。特别是，如果把其他算法的解作为遗传算法初始群中的个体，往往能获得更好的解，缺点是遗传算法执行时间比其他调度算法长得多［3，4］。

本文是在一种基于遗传算法的仓储车辆调度方法的启发下［5，6］，提出了一种基于贪心算法和遗传算法的仓储车辆调度算法。不仅克服了遗传算法在任务调度上的编码限制，而且贪心算法的加入使得融合算法性能大大提高。此算法还可以应用在多任务多处理器求最短完成时间的静态调度方面。

1 相关理论

仓储车辆调度属于多任务多处理器调度的一种，可分为任务分配和任务排序两部分。此前已有学者采用遗传算法解决该问题。该调度方法编码复杂，并且由于其遗传算法的交叉和变异过程极易产生非可行解的个体，这些个体经修正后随机性降低，算法的全局搜索能力大大减弱。本文的算法采用遗传算法优化任务分配，采用贪心算法优化任务排序。贪心算法的加入不仅使得遗传算法在个体编码简化和运行时间缩短，同时排除了不可行解的出现，并增强了全局搜索能力。

1.1 贪心算法

贪心算法是一种常用的求解最优化问题的简单、迅速的方法。贪心算法总是做出在当前看来最好的选择，它所作的每一个选择都是在当前状态下某种意义的最好选择，即贪心选择，并希望通过每次所作的贪心选择最终得到问题最优解［7］。贪心算法是一种快速简易的求解旅行商问题(traveling salesman problem，TSP)的方法［8，9］，其求解的基本思想是优先选择当前点的最短边。每次选择边的规则为

1)不会引起顶点度数大于等于3;

2)除非选取的边为最后一条边，所选取的边不应形成回路。

本文贪心算法是当每辆车分配到任务后，对任务执行的先后进行排序，获得单个车辆完成任务的最优解。单车辆的任务排序可视为一种TSP。经任务分配后，单车辆任务量不大，即TSP中途经点较少的情况下，贪心算法十分适用此排序问题。

1.2 遗传算法

遗传算法是一种通过模拟自然进化过程，搜索最优解的方法，具有隐式并行性和很好的全局寻优能力。遗传算法基本操作过程如图1所示，其构成要素主要包括计算适应度、选择算子、交叉算子和变异算子［10］。

图1 遗传算法基本操作流程Fig 1 Basic operation flow chart of genetic algorithm

本文采用遗传算法寻求最优的任务分配方式，个体的基因型仅表示调度方法的任务分配。当判定个体适应度时，根据分配的任务采用贪心算法依次求得每辆车的执行时间。使用遗传算法的好处在于，无论初始化、交叉、变异得到的基因型都不会存在不可行解，确保了随机性和全局搜索能力。

2 算法实现

本文的算法是以遗传算法为框架，应用贪心算法简化其编码复杂度和计算适应度。最优解的求解过程依赖于遗传算法。遗传算法实现流程如图2所示。计算适应度环节主要使用贪心算法，对每辆车分配的任务进行查表的方式获得执行时间最短的任务排序，同时获得并记录其个体代表的调度方案的执行时间，从而求得个体适应度。

图2 遗传算法实现流程Fig 2 Realization flow chart of genetic algorithm

2.1 遗传算法的定义与设置

遗传算法在编码设计中常采用二进制编码、格雷码和浮点编码等。本文采用整数编码，所需调度任务数为Nt，可调度车辆数为Nv。个体的染色体可编码为:长度Nt位，每位Nv种基因型。将所有任务编号为0，1，2，…，(Nt-1)，车辆编号为0，1，2，…，(Nv-1)。例如:有 8 项运输任务和4辆可调度车，每个个体编码为一个8位字串x∈{0，1，2，3}，其中每位有4种编码选择。个体型与对应分配方式如表1。

表1 8任务4车辆编码示例Tab 1 Coding example of 8 tasks of 4 vehicles

每个个体代表一个调度方案，此编码的个体型只能反映调度中的分配方案，具体调度方案需要经过贪心算法得到。

选择算子采用确定式采样(deterministic sampling)选择。设群体大小为M，个体i的适应度为Fi。群体中每个个体在下一代群体中的期望生存数目Ni

用Ni的整数部分⎿Ni」确定各个对应个体在下一代群体中的生存数目。由该步共可确定出下一代群体中的个个体。按照Ni的小数部分对个体进行降序排序，顺序取前个个体加入到下一代群体中。至此可完全确定出下一代群体中的M个个体［11］。

交叉算子采用单点交叉(one-point crossover)。经确定式采样选择好的个体，以交叉概率Pc参与交叉操作。在参与交叉操作的个体编码中随机设置一个交叉点，然后在该点相互交换2个配对的个体部分的染色体。

变异算子采用均匀变异(uniform mutation)。个体编码串中每一个基因座都为变异点，每个变异点以较小的变异概率Pm从符合的基因范围内取一随机数来替代原有基因值。

选择算子会让适应度更高的个体更多地保留，交叉、变异等操作产生出新的优良个体。但由于这些操作的随机性，它们也可能破坏原有适应度较好的个体。如图2所示，新一代群体中会保留上一代群体中适应度最高的个体，该操作保证了遗传算法的收敛性并加快了进化的效率。

2.2 贪心算法与适应度

贪心算法主要应用在根据已有任务分配下，计算车辆最短所需的执行时间。个体的执行时间是评判该个体优劣的主要依据，所需的执行时间越长，说明该方案越差，个体的适应度也越低。仓库中的运输车辆如同多台可并行执行任务的处理器，为了实现资源优化利用，调度者希望尽可能多地利用车辆，最好每辆运输车都分配有任务，达到车辆资源的充分利用。因此，本算法在求最后适应度值时，增加了罚函数，对于出现不均分配的个体予以适应度上的惩罚。

计算适应度环节流程如图3，可细分为:

1)对个体编码串进行解码，即按照编码串对调度车辆进行任务分配;

2)贪心算法求得每辆运输车完成所分配任务预计执行最短的时间;

3)取个体中最长的执行时间，作为整个调度方案的执行时间;

4)根据调度方案的执行时间T和罚参数P，求解适应度函数如下

其中，Pi为调度方案i中有Pi辆调度车未被分配任务。

图3 计算适应度流程Fig 3 Flow chart of calculating fitness

个体基因先通过解码得到任务分配情况，再由贪心算法通过查表对任务进行排序求每辆车执行时间。设3辆可调度车编号为A，B，C，6项需执行任务编号为ⅰ，ⅱ，ⅲ，ⅳ，ⅴ，ⅵ。表2中每个单元格数值表示，完成横向任务后再去处理纵向任务所需要花的时间值;横向为车编号代表，由车辆初始位置执行纵向任务所需要花的时间值。时间值设置为1～100 min。

表2 执行时间表Tab 2 Executing time table

例如:个体222110对其使用贪心算法，查表求解最短执行时间，其步骤如下:

1)由解码得A车处理任务ⅵ，B车处理任务ⅳ和ⅴ，C车处理任务ⅰ，ⅱ和ⅲ。

2)以C车为例，查C车初始位置执行ⅰ，ⅱ，ⅲ的时间值选取最小，先执行。如表2选取ⅱ先执行，查询ⅱ完成后ⅰ，ⅲ的时间值选最小ⅰ。最后查得ⅰ完成后执行ⅲ所需时间，得此调度方案下C车的最佳任务排序为ⅱ→ⅰ→ⅲ，时间值为2+10+43=55 min。同理求得A车任务排序ⅵ，时间值89min;B车任务排序ⅴ→ⅳ，时间值66 min。

3)个体222110对应的调度方案执行时间取最长的A车，时间值89 min。

4)按式(2)求出该个体适应度为2.110。此处保留三位小数。

由上可见:贪心算法由一个仅表示任务分配的遗传算法个体编码串，经过解码、贪心算法求解、适应度函数，形成了一个完整的调度方案。用最快速、简便的方法在极短的时间里给出了最优或是次优的任务排序解。获得每个任务由哪辆车完成，每辆车先后执行哪些任务，预计需要多少时间等信息。

3 实验和结果分析

实验程序设3辆可调度车编号为A，B，C，6项需执行任务编号为ⅰ，ⅱ，ⅲ，ⅳ，ⅴ，ⅵ。各任务执行时间值如表2。种群大小M设置为M=NtNv×2=36。进化代数Ge=100代，交叉概率Pc=0.7，变异概率Pm=0.01。初代个体编码串与时间值表(表2)均为随机数产生。图4显示了此算法在进化中，种群的平均时间值和最优个体时间值的变化过程。由图可见，遗传算法在前40代，种群的平均时间值明显下降，意味着整个种群在向更优进化。由于该算法使用了最优保存策略，故最优个体时间值折线不像平均时间值那样呈现波动进化。除非当进化中产生更优个体才会替换原有的，时间值从而进一步降低，否则，一直保持下去。该例最后一代种群的最优个体，即算法的最终解为:

个体基因:012011;

A车:ⅰ→ⅲ，时间值51 min;

B车:ⅴ→ⅱ→ⅵ，时间值52 min;

C车:ⅳ，时间值16 min;

调度时间值:52 min。

图4 不同进化代数的时间值变化Fig 4 Time value change of different numbers of evolution generation

算法中进化代数Ge与种群大小M都是随着调度量的需求而变化的。经实验发现，尤其种群数量M极大影响着算法的搜索能力。若M设置过小，遗传算法容易早熟，全局搜索能力明显变差。相较而言代数Ge的变化，只是影响已有种群中发生交叉、变异等操作发生的概率。因此，当M不大或Pc，Pm设置较小时，Ge变化的作用并不明显。若把种群数量缩小一半至18进化情况见图5。平均时间值折线显示种群较早就停止进化，有明显的早熟现象。且最终解的时间值为57 min，并非最优调度方案。可见种群数量M的缩小使得搜索能力大大减弱。

图5 种群数量缩小一半的时间值变化Fig 5 Time value change of half population quantity

若保持M=36，将进化代数减少一半至50，进化情况见图6。由平均时间值折线可见，进化情况与图4相似，并未产生早熟现象。通过50代的进化也获得了最优调度方案。为确保进化完整和适应更大调度量，进化代数应设置得足够大。

4 结论

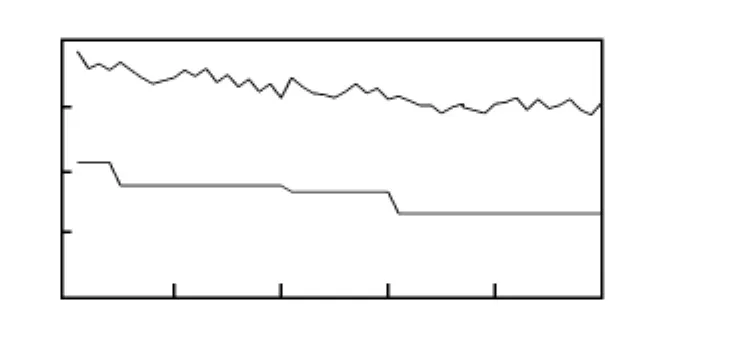
图6 遗传代数减少一半的时间值变化Fig 6 Time value change of half inheritance generations

本文提出的基于贪心算法和遗传算法的仓储车辆调度算法，经编程实现与实验证明:本方法简化了遗传算法对车辆调度应用中复杂的编码方法。避免了由于约束条件而将个体调整为可行解时而产生的非随机性，不仅避免遗传算法易出现的早熟的困境，也提高全局搜索能力。本算法的交叉、变异等操作使用起来更加灵活，限制更少，使用者可根据使用范围，选择更适用的操作种类。本算法还可通过改动任务、时间表、罚函数等，以适用于其他更高要求的多任务多处理器的调度。

［1］钟一文，杨建刚.求解多任务调度问题的免疫蚁群算法［J］.模式识别与人工智能，2006，19(1):73-78.

［2］Sapkal SU，Laha D.An improved scheduling heuristic algorithm for no-wait flow shops on total flow time cirterion［C］∥2011 the 3rd International Conf on Electronics Computer Technology，2011:159-163.

［3］Gupta S，Agarwal G，Kumar V.Task scheduling in multiprocessor system using genetic algorithm［C］∥2010 the 2nd International Conf on Machine Learning and Computing，2010:267-271.

［4］Correa R C，Ferreira A，Rebreyend P.Scheduling multiprocessor tasks with genetic algorithms［J］.IEEE Trans on Parallel and Distributed Systems，1999，10(8):825-837.

［5］郭小溪.RFID室内仓储车辆的智能导航与调度技术［D］.杭州:浙江大学，2011:4-8.

［6］韩晓路.基于局部搜索遗传算法的仓库车辆调度优化研究［J］.物流技术，2011，30(4):65-67.

［7］魏英姿，赵明扬，黄雪梅，等.求解TSP问题的贪心遗传算法［J］.计算机工程，2004，30(19):19-34.

［8］Chakraborty N，Akella S，Wen JT.Coverage of a planar point set with multiple robots subject to geometric constraints［J］.IEEE Trans on Automation Science and Engineering，2010，7(1):111-122.

［9］王晓东.计算机算法设计与分析［M］.北京:电子工业出版社，2004:134-142.

［10］陈国良.遗传算法及其应用［M］.北京:人民邮电出版社，1996:51-98.

［11］周 明，孙树栋.遗传算法原理及应用［M］.北京:国防工业出版社，1999:47-48.