稀疏台网反演区域地震偏量矩张量解的稳定性＊

郑建常 陈运泰

1）中国北京100081中国地震局地球物理研究所

2）中国济南250014山东省地震局

稀疏台网反演区域地震偏量矩张量解的稳定性＊

郑建常1，2），陈运泰1）

1）中国北京100081中国地震局地球物理研究所

2）中国济南250014山东省地震局

使用区域地震台网的波形资料，研究了2010年2月26日台湾以东海域MW5.4地震的偏量矩张量，所得结果与Havard CMT目录给出的解之间的Kagan角为9.5°，两者较为一致；反演得到这次地震的震源深度为41km，接近USGS给出的定位结果，可能更接近真实的震源深度.选择不同的台站组合，分析了台站布局对矩张量解的影响.结果显示，3个台站的组合基本上都可以较为准确地得到矩张量解，台站方位覆盖越好，反演得到的解的偏差越小；在合适的情况下，两个台站的组合也可以得到较为可靠的解.

偏量矩张量 稀疏台网 离散波数法 波形反演

引言

对全球较大的地震（矩震级MW≥5.5），哈佛大学的全球矩心矩张量（Global Centroid Moment Tensor，简写为GCMT）项目组使用全球地震台网记录的大于45s的长周期波计算矩心矩张量（Dziewonskiet al，1981），美国地质调查局（USGS）基于周期T≥15s的体波分析矩张量（Sipkin，1982；Sipkin，Needham，1989），东京大学地震研究所使用周期在45—100s之间的波形也在做类似的分析，并且实现了准实时的自动处理（Kawakatsu，1995）.这些研究都使用远震波形，并且只有在几千千米外能产生足够能量信号的强震才能进行分析.

现代的区域宽频带数字地震台网使得在区域范围内（震中距1°—10°）反演较小地震的矩张量成为可能（Dreger，Helmberger，1993；Retsima，Lay，1993；Romanowiczet al，1993；Braunmilleret al，1995；Nábělek，Xia，1995；Randallet al，1995；Thio，Kanamori，1995；Ammonet al，1998）.与远震相比，区域地震和地方震的矩张量反演更为复杂：在较近的震中距内，波形含有丰富的高频信号，由波的干涉产生的波（如Lg波）可能在记录中占主导地位，并且其近场效应可能非常强.在远震研究中为计算合成地震图而采用的射线理论计算方法，不得不用能重现整个波场的全波形方法替代.

20世纪90年代以来，区域矩张量反演方法得到了很大的发展.Patton和Zandt（1991）首先对用于远震的面波反演算法进行修改使之适用于区域性地震；Dreger和Helmberger（1993）提出了区域地震和地方震的时间域矩张量反演算法；Randall等（1995）基于Langston（1981）提出的时间域反演方案，使用Kennett（1983）的反射矩阵法计算格林函数，由区域3分量的位移记录计算偏量矩张量；Cameron等（2006）对该方法进行了改善，并用于研究加勒比海地区海啸预警问题；Romanowicz等（1993）以及Thio和Kanamori（1995）等对美国西部地区的中等地震开展了常规的区域矩张量分析；Ritsema和Lay（1995）使用周期大于35—50s的区域长周期地动记录反演了美国西部MW＞4.5的地震矩张量；Pasyanos等（1996）比较了区域面波反演和时间域矩张量反演方法的结果，并进行了中等地震矩张量解的准实时处理的尝试.Braunmiller等（2002）使用区域台网资料，计算了欧洲—地中海地区的较强地震的矩张量解，并对解的可靠性进行了讨论.Kubo等（2002）检查了日本防灾科学技术研究所（National research Institute for Earth science and Disaster prevention，简写为NIED）的区域矩张量目录的质量，使用合成数据检验了区域矩张量解的稳定性，并讨论了数据噪声以及速度结构和震中位置的误差对解的影响.Ichinose等（2003）使用不同的速度结构模型，对美国加利福尼亚东部和内华达州西部的MW≥4.0地震进行了矩张量计算，并研究认为在方位角的分布较为均匀的情况下，至少3个台站就可以得到较好的矩张量解，且P和T轴方向的偏差可在10°以内.Zahradnik等（2008）使用全波形数据反演了希腊地区6次MW4.0左右的中等地震的矩张量，并就增加矩张量解的稳定性问题进行了详细讨论.Scognamiglio等（2009）发展了时间域地震矩张量反演的自动确定和修正方法，并对意大利地区M≥3.5的近震或区域性地震事件进行了矩张量分析.

对于区域性地震，经常可能遇到的一个问题是由于噪声、台站布局等因素造成的可用台站数不足.Dreger和Helmberger（1993）专门研究了稀疏台网下区域地震矩张量的反演方法；Walter（1993）使用周期15—50s的单台3分向区域性地震的记录波形，研究了内华达州一次mB5.5地震的震源机制；Godano等（2009）使用稀疏台网的振幅数据非线性反演震源机制的研究表明，对大多数3个3分向台的组合，可得出正确的解，并且震源机制中走滑成分越高，对解的约束就越好.

据中国地震台网测定，2010年2月26日01时07分58.7秒（协调世界时，UTC），在台湾以东海域发生了MS5.1地震，中国地震台网给出的震中位置位于23.8°N，122.8°E.对这次地震，世界上多个有关的研究机构都独立给出了震源位置和矩张量解，这些结果之间多少存在一些差异，详细比较见表1.本文以这次地震为例，进行了区域矩张量反演，并在此基础上选择不同的台站组合讨论稀疏台网对矩张量解稳定性的影响.

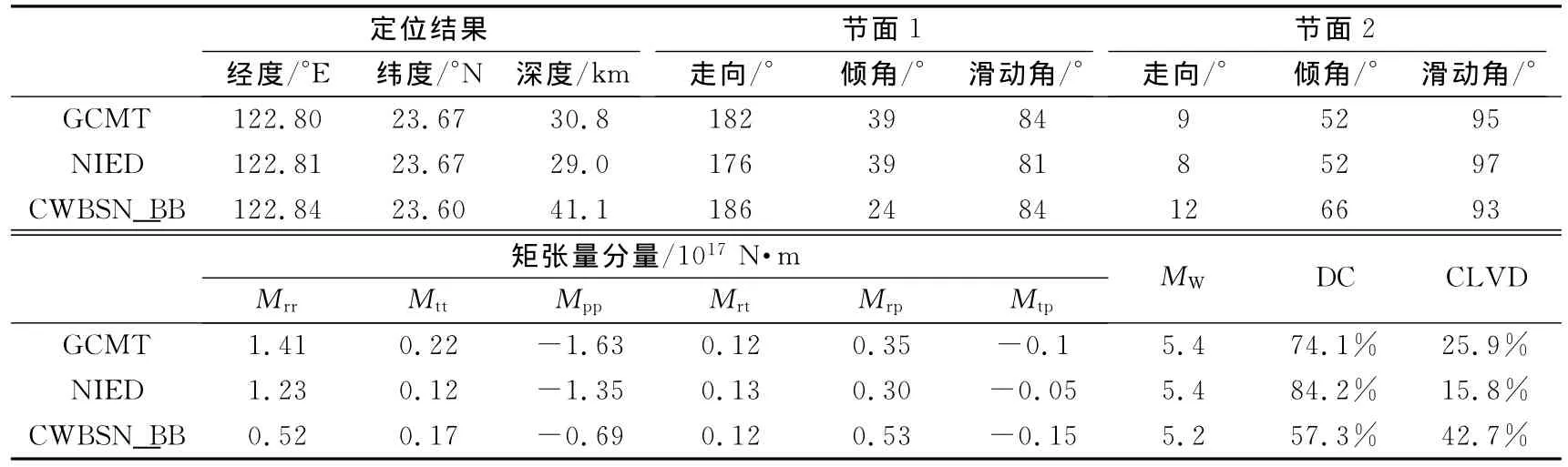
表1 不同机构给出的2010年2月26日台湾以东海域M5.4地震矩张量解比较Table 1Moment tensor solutions for the 26Febuary 2010 M5.4earthquake in Taiwan adjacent area by different institutions

为了分析本文得到的解的变化程度，选取哈佛大学全球矩心矩张量目录（GCMT）给出的震源机制作为参考解，使用Kagan（1991）定义的不同震源机制间的最小旋转角（Kagan角），计算本文得到的震源机制结果与CCMT参考解之间的Kagan角，用以衡量解的稳定程度.

1 数据与方法

1.1 数据

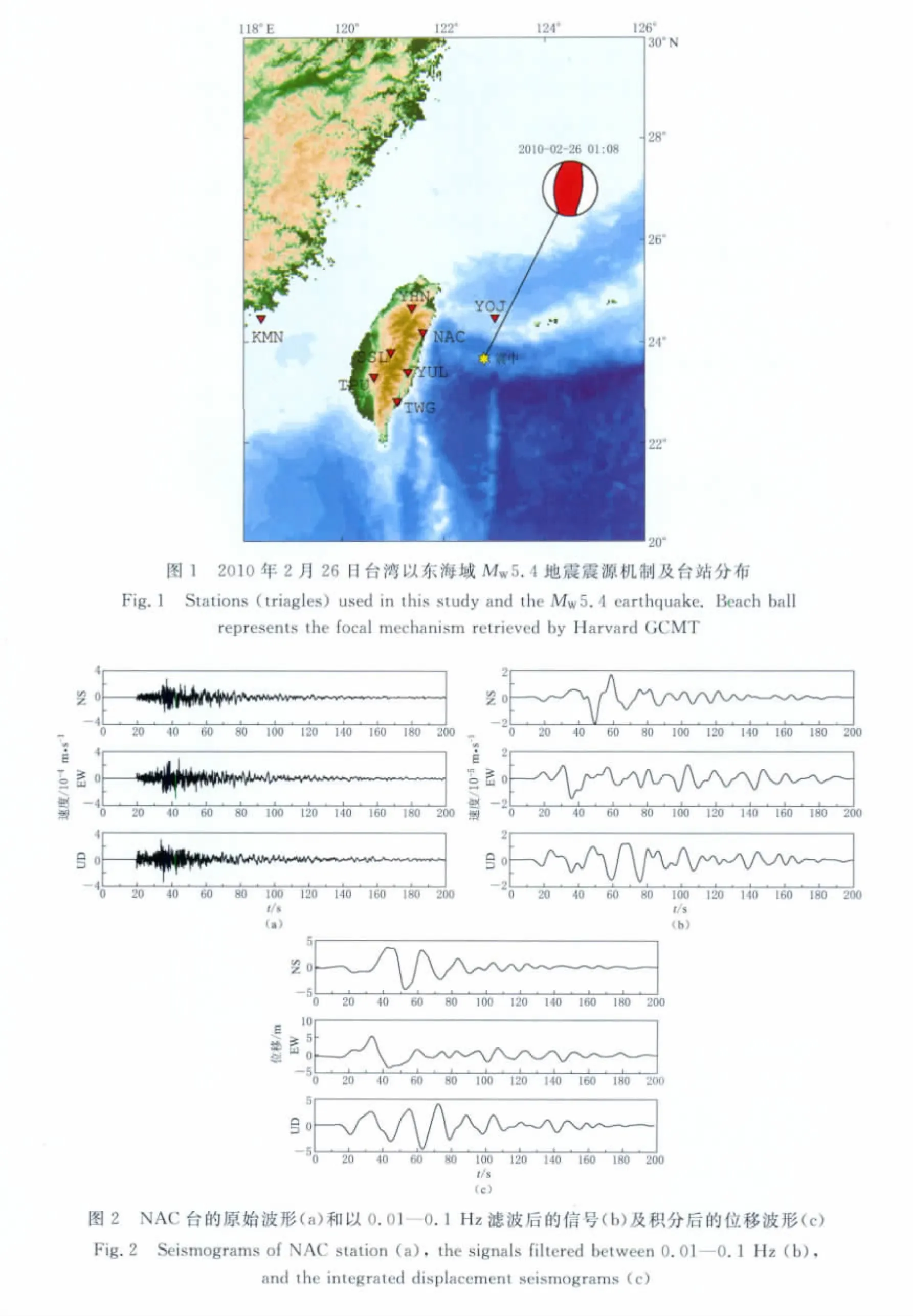
这次地震发生在琉球岛弧外侧，距离台湾岛最近约120km.我们使用来自于IRIS网站的波形数据，在震中距5°范围内主要有台湾宽频带地震台阵（Broadband Array in Taiwan for Seismology，简写为BATS）的7个台，分布在地震的西侧，以及日本气象厅地震台网（Japan Meteor－ological Agency Seismic Network）的YOJ台，位于地震的北侧.地震及台站分布见图1.

原始波形为速度记录，在计算过程中首先进行仪器校正，然后在0.01—0.1Hz的带宽进行带通滤波，加5%的余弦边瓣.图2给出了NAC台的3分向记录以及滤波和积分后的波形.将速度记录积分转换成位移，对位移进行反演.台湾的KMN台由于记录积分后出现漂移，所以没有使用该台的资料.

GCMT给出了这次地震的震源机制，见图1.日本防灾科学技术研究所（NIED）使用日本地区宽频带地震台网给出的此次地震的震源机制，与哈佛大学的结果非常接近，二者之间的Kagan角为3.43°，矩张量解的参数见表1.台湾的“中央气象局”（Central Weather Bureau，简写为CWB）根据台湾的宽频地震网（CWBSN＿BB）使用Kao和Jian（2001）发展的矩心矩张量求解方法也得出此次地震的矩张量解.这3个机构得到的震源机制解的对比情况见表1.

对这次地震，台湾的“中央气象局”（CWB）给出了台网定位位置：23.69°N，122.87°E，震源深度52.1km，震级为M5.8.与该机构的矩张量反演得到的矩心位置存在一定的差异，美国地质调查局（USGS）给出的震源位置：23.79°N，122.85°E，深度39.3km，体波震级mB5.5，与其它的定位结果偏差较大.日本气象厅（Japan Meteorological Agency，简写为JMA）的地震目录给出的此次地震震源位置：23.7°N，122.8°E，深度50km，震级为MJ5.7.

由此可见，不同机构给出的这次地震的震中位置存在较大差异，不单在水平方向上相差几十千米（水平方向上的差别更多表现在纬度上），深度差异也十分明显：GCMT和NIED给出的深度都在30km左右，USGS和CWBSN＿BB给出的深度在40km左右，而JMA和CWB的台网定位结果给出的深度都在50km.由于此次地震发生在琉球岛弧的外侧，精确地测定此次地震的深度及震源机制，有助于详细了解和深入研究该区域的大地构造.因此我们使用图1所示的7个台站的宽频带数据求解这次地震的矩张量.Kubo等（2002）使用合成数据的检验表明，在水平方向上，即使定位误差超过0.1°，区域矩张量解仍然相当稳定.说明在水平成层介质模型下，矩张量对震中位置的不精确不敏感.对比几个定位位置可以看出，虽然GCMT和NIED使用了不同范围的台站和不同频率区间的波形，但二者得到的震中位置非常接近.因此我们选用了GCMT给出的震中位置，只在深度方向上进行搜索.

1.2 区域矩张量分析方法

地球内部的任意震源可以表示为6个独立分量的矩张量.该矩张量可以分解为双力偶（double couple，简写为DC）分量和非DC分量，非DC分量包括各向同性体积分量（isotropic，简写为ISO）和补偿线性矢量偶极子分量（compensated linear vector dipole，简写为CLVD）.双力偶分量描述的是各向同性介质中的沿断层面发生的剪切滑动，通常被接受为构造地震的震源模型.在一些情况下，震源机制可能偏离双力偶模型，在矩张量中表现为非DC分量部分.本文强制约束矩张量解中的ISO分量为零，进行偏量矩张量的反演.

Kikuchi和Kanamori（1991）提出了迭代反褶积方法来计算远震的矩张量解.类似他们的方法，我们考虑区域地震的矩张量反演，使用Bouchon（1981）的离散波数法计算格林函数.对于中等地震而言，由于震源破裂时间较短，可以用狄拉克－δ函数来表示震源时间函数.并且研究表明，在矩张量反演过程中震源时间函数的长度主要影响标量地震矩的大小（Cescaet al，2006）.在这种情况下，合成位移地震图由6种基本震源机制对应的基本地震图组合来近似（Kikuchi，Kanamori，1991）：

式中，Ei（t），i＝1，2，…，6，为6种基本地震图，ai为待求解的系数.

系数ai与矩张量Mij有关，在地理坐标（朝北为正，朝东为正，朝上为正）下：

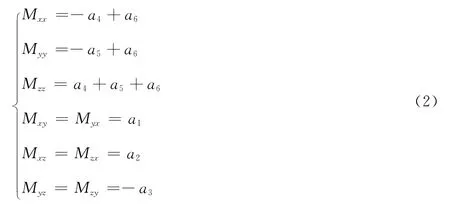
矩张量Mij的特征矢量提供了断层机制的走向、倾角、滑动角，特征值提供了标量地震矩，并将矩张量分解为3个部分：DC＋CLVD＋ISO.在偏量矩张量反演情况下，令各向同性体积分量为零，即系数a6＝0.

使用最小二乘法求解反演问题，使得观测波形与合成波形之间的错配程度最小.错配函数定义如下：

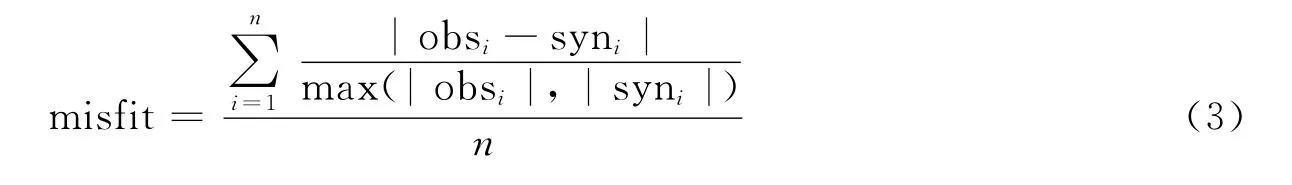
式中，obsi为观测波形，syni为合成波形，i＝1，2，…，n，n＝台站数×分向数×使用频率数.

运用网格搜寻法搜寻预先设定的尝试震源位置和时间平移，以确定最优结果.通过搜索得到最小二乘法误差最小的解，即合成波形与观测波形相关程度最好.

1.3 地壳结构模型

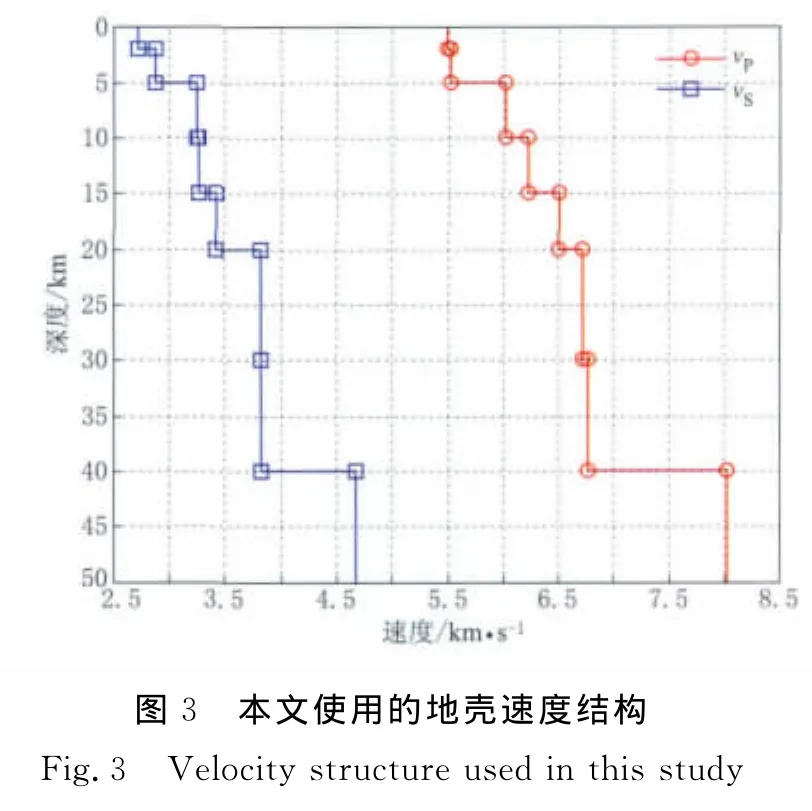
由于地震发生在琉球岛弧，此处由于菲律宾板块的俯冲作用地壳略有增厚（李志伟等，2007）.参考Rao和 Wu（1995），Ma等（1996），以及 Kim 等（2005）对台湾地区地壳结构的研究成果，本文使用如图3所示的地壳速度模型.

1.4 双力偶震源机制的最小旋转角（Kagan角）

用于描述震源受力情况的双力偶震源模型的T，P，B轴彼此正交，构成了以震源为原点的三维坐标系.在保持应力轴手性顺序的情况下，Kagan（1991）利用正交矩阵和四元数代数给出了任意两个双力偶模型之间的三维空间最小旋转角的计算方法，表示了震源球上两个不同震源机制之间的偏转程度，称为Kagan角（例如，对于同一断层，左旋走滑和右旋走滑两种机制之间的Kagan角为90°）.这一概念已经被应用到了有关震源机制研究的工作中（Kubo，Fukuyama，2002；Okal，2005；Pondrelliet al，2006）.有关Kagan角的推导和求解详见Kagan（1991，2007）的有关论文.

2 结果与分析

2.1 台湾以东海域5.1级地震震源机制

使用台湾台网的6个台（YHN、NAC、SSL、YUL、TPU、TWG）和日本的YOJ台的波形资料进行了矩张量反演.选用的频带宽度为0.01—0.1Hz.台站方位角的缺口为227.49°.震中位置选用GCMT目录给出的结果，在深度方向上进行搜索，起始深度为5km，步长为2km，共24个搜索深度，最深到51km.

计算得到的标量地震矩9.327×1016N·m，相当于矩震级MW5.4；震源机制解：节面A的走向192°，倾角37°，滑动角100°；节面B的走向0°，倾角53°，滑动角83°.

图4给出了本文使用这7个台的资料得到的矩张量解，以及不同深度搜索得到的最优解的错配值变化曲线.我们得到的结果与GCMT目录给出的解十分接近，两个震源机制解之间的Kagan角为9.46°.

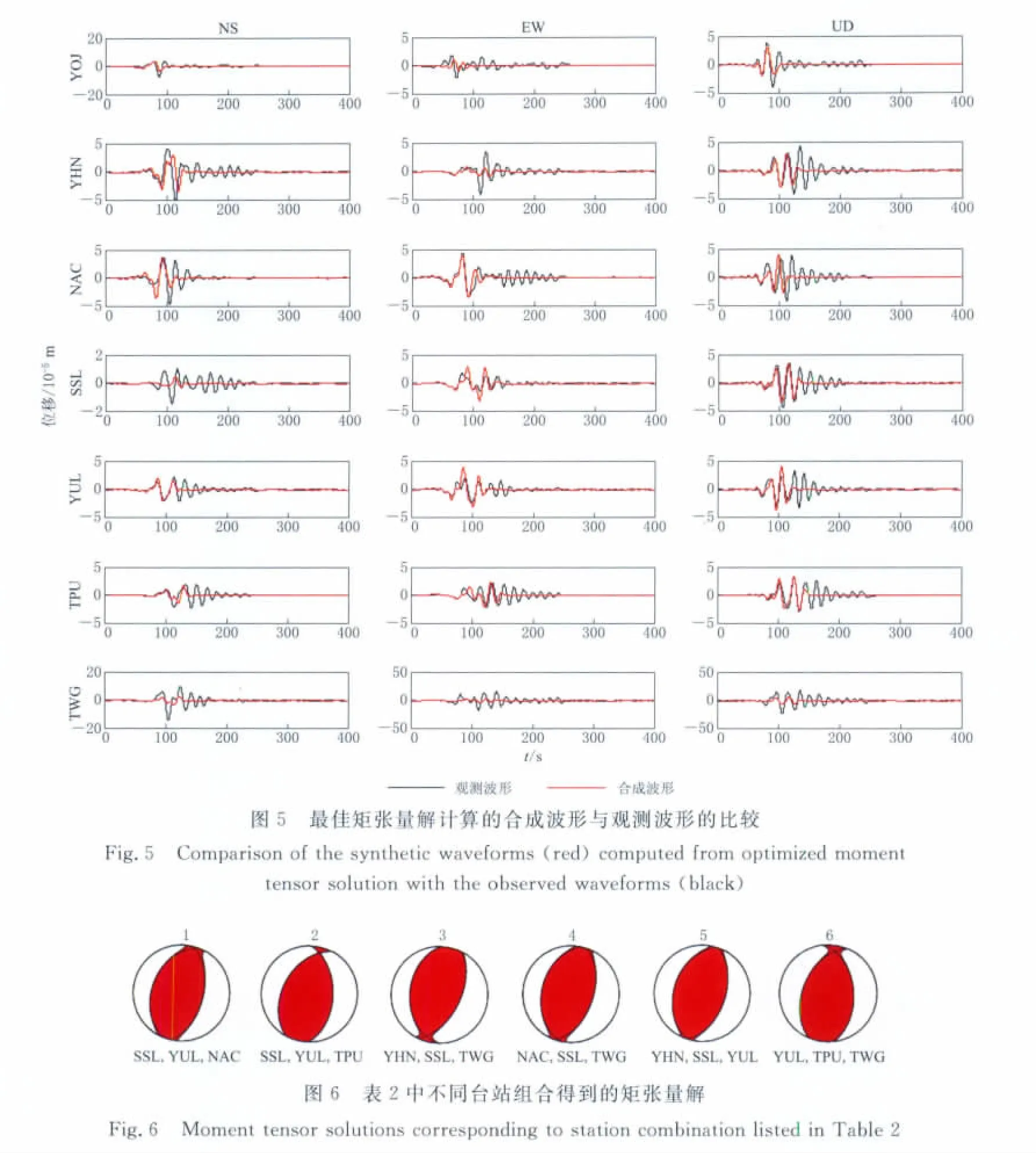
观测波形与合成波形的拟合结果见图5.由图5可见，波形的前半段拟合效果较好；由于使用了比较简单的一维速度模型，后半段的尾波部分拟合情况较差.

2.2 3个台的组合

选择了部分3个台站的组合来计算矩张量解，结果见表2和图6.

由表2可见，由3个台站的组合，基本都可以得到较为准确的矩张量解.其中，台站分布覆盖的方位角张角较小（≤30°）的台，得到的震源机制与GCMT给出的解的Kagan角在20°范围以内；而台站覆盖的方位角张角较大（≥30°）的组合，得到的解与GCMT解的Kagan角在15°范围以内.矩震级结果的差基本在0.1级以内.因此认为，布局较好的3个台可以得到较为准确的区域地震的矩张量解.

表2 不同台站组合的矩张量结果比较Table 2 Summary of inversion results using different station combination

与前面7个台的资料得到的结果相比，这几组3个台的组合结果的Kagan角都在15°的范围内，说明3个台的组合得到的结果较为稳定.

2.3 两个台站的组合

在所用的7个台中随机选取两个台的资料进行反演求解矩张量.表3给出了所有台站组合的情况，以及其张角、方位角空白、最佳解的矩心深度，矩张量解与GCMT结果的最小旋转角等.图7给出了这21种组合得到的矩张量解.

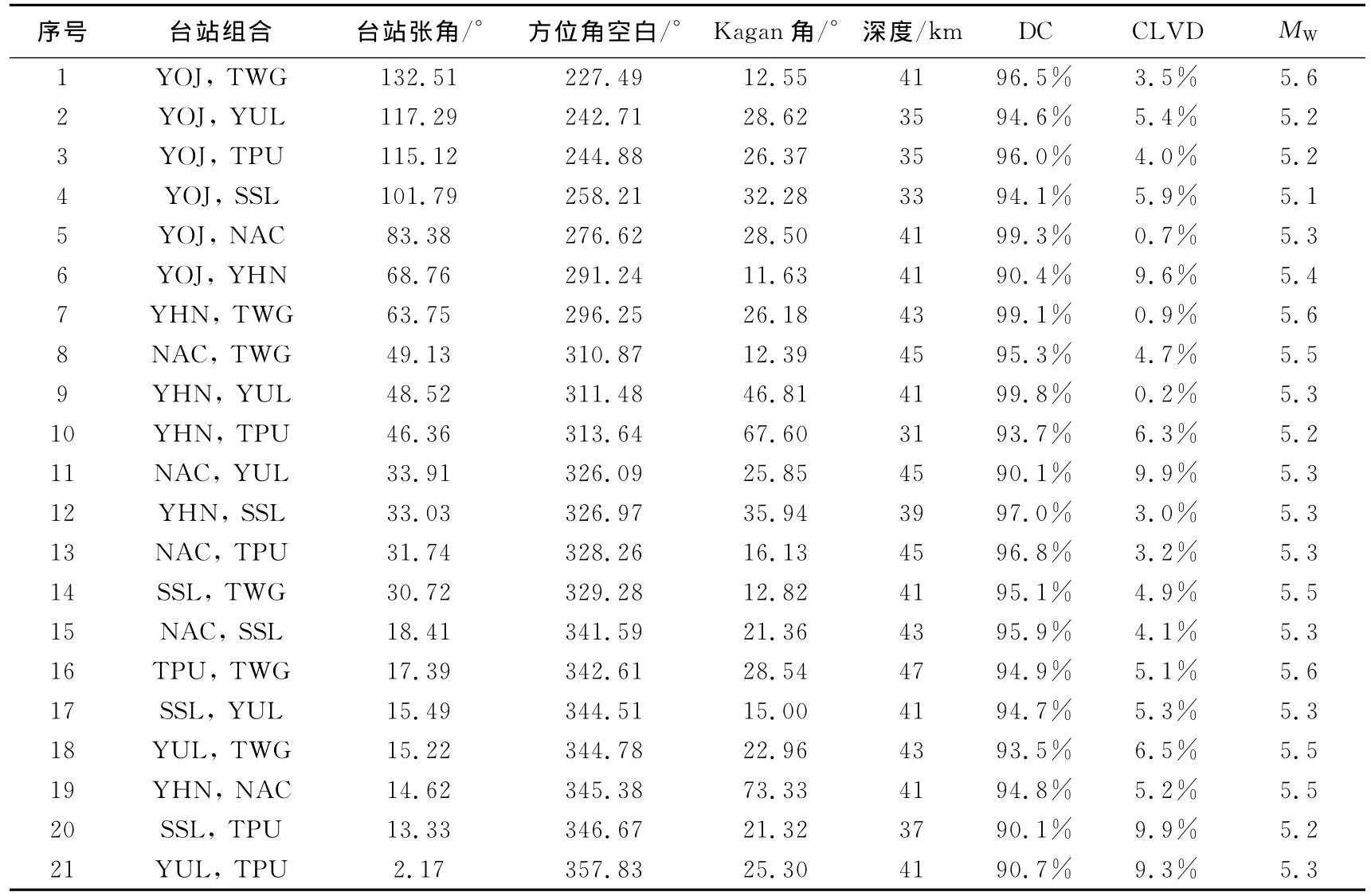
表3 不同台站组合得到的矩张量结果及其参数Table 3 Parameters and results of moment tensor inversion using different station combination

图8和图9分别给出了YUL、NAC台和YHN、NAC台得到的矩张量解的波形拟合情况.由图可见，吻合得相对也较好.

统计分析了由两个台站得到的矩张量解的Kagan角的分布情况，见图10.其中，Kagan角≤15°的解占23.8%；Kagan角在20°—30°之间的占47.6%；Kagan角在30°以内的解占所有解的76.2%.

分析各台的不同组合的平均Kagan角（表4），可见除YHN台和TPU台以外，其余台的平均值都在30°以内，TPU台也刚刚超过30°.唯一例外的是YHN台，该台与其它台的组合得到的解与GCMT结果的平均偏离超过了40°.该台位于断层面解的节线附近，这一现象可能与该台所处的位置有关.

3 讨论与结论

基于台湾和日本的7个3分向宽频带地震台，应用全波形区域矩张量反演方法得到了2010年2月26日台湾以东海域MW5.4地震的偏量矩张量.得到的结果与哈佛大学GCMT目录以及日本防灾科学技术研究所（NIED）给出的解较为一致.其中与GCMT解的Kagan角为9.46°，与NIED解的Kagan角为11.04°.在GCMT给出的震中位置上对深度进行搜索，结果得出震源深度为41km.

表4 各台参与台站组合的矩张量解的平均Kagan角Table 4 Average Kagan angle for individual stations used

选择分布不同的3个台站的组合，结果显示基本上都可以得到较为准确的矩张量解.其中，台站分布覆盖的方位角张角较小（≤30°）的台，得到的震源机制与GCMT给出的解的Kagan角在20°范围内；而台站覆盖的方位角张角较大（≥30°）的组合，得到的解与GCMT解的Kagan角在15°范围内.可以认为由3个台站的组合得到的解较为稳定.

研究了两个台站的所有组合求解矩张量解情况.统计结果显示：Kagan角≤15°的解占23.8%，Kagan角在30°以内的解占所有解的76.2%.这说明在合适的情况下，用两个区域性的地震台求解，也可以得到较为准确的矩张量解.

由于此次反演使用的台站的震中距除YOJ台为77.13km外，其余6个台站的震中距均在120—250km之间，台站记录的信噪比均大于100dB.因此可以认为波形受噪声水平干扰很小，接近于理想的地震图.由图7和图8可见，矩张量解可以很好地拟合观测波形前半部分的震相，说明本文给出的速度结构也比较合适.至于观测波形的尾波部分，我们认为这些震相反映的是更精细的地下介质的情况，由于我们使用的地壳模型比较简单，未能准确地拟合这些更加复杂的震相.

本文反演得到的矩张量解与GCMT、NIED及CWB的结果基本一致，但仍存在一些细微的差异.Dreger和Helmberger（1993）认为全球与区域矩张量结果的差别可能是由于台站覆盖不完整，影响了反演过程中对局部最小值的认定，或者来自于不正确的速度模型以及定位的不准确等所致.从本文的结果来看，在观测资料较好的情况下，使用3个台站的波形资料时，矩张量解的稳定性范围在15°的范围内.本文使用区域资料在同一震中位置上进行矩张量反演得到的该地震震源深度为41km，与USGS以及CWBSN＿BB得到的结果非常一致，而与GCMT和NIED以及JMA的结果存在大约10km的误差.由于GCMT使用远震波形和PREM模型，对深度的分辨率可能不如区域波形资料的分析，因此我们认为本文得到的深度结果可能更接近真实的地震震源.

本文使用的波形资料来自于IRIS网站.中国地震局地球物理研究所许力生研究员以及刘超博士对有关工作给予了帮助；审稿人提出了宝贵的修改意见和建议.作者在此谨致谢忱！

李志伟，胥颐，郝天珧，刘劲松.2007.利用非线性方法反演琉球—台湾—吕宋地区的岩石层P波速度结构［J］.地球物理进展，22（5）：1345－1351.

Ammon C J，Herrmann R B，Langston C A，Benz H.1998.Source parameters of the January 16，1994Wyomissing Hills，Pennsylvania earthquakes［J］.Seism Res Letters，69（3）：261－269.

Braunmiller J，Leitner B，Nábělek J，Leitner B，Qamar A.1995.The 1993Klamath Falls，Oregon earthquake sequence：source mechanisms from regional data［J］.Geophys Res Lett，22（2）：105－108.

Braunmiller J，Kradolfer U，Baer M，Giardini D.2002.Regional moment tensor determination in the European－Mediterranean area－initial results［J］.Tectonophysics，356（1－3）：5－22.

Bouchon M.1981.A simple method to calculate Green＇s functions for elastic layered media［J］.Bull Seism Soc Amer，71（4）：959－971.

Cameron A E，Asencio E，Huérfano V，Mendoza C，von Hillebrandt C.2006.Source parameters analysis of the regional moment tensor inversion in the Caribbean region［J］.Seism Res Lett，77（2）：288.

Cesca S，Buforn E，Dahm T.2006.Amplitude spectra moment tensor inversion of shallow earthquakes in Spain［J］.Geophys J Int，166（2）：839－854.

Dreger D S，Helmberger D V.1993.Determination of source parameters at regional distances with single station or sparse network data［J］.J Geophys Res，98（5）：8107－8125.

Dziewonski A M，Chou T A，Woodhouse J H.1981.Determination of earthquake source parameters from waveform data for studies of global and regional seismicity［J］.J Geophys Res，86（B4）：2825－2852.

Godano M，Marc R，Anne D，Thomas B，Emmanuel G.2009.Focal mechanisms from sparse observations by nonlinear inversion of amplitudes：Method and tests on synthetic and real data［J］.Bull Seism Soc Amer，99（4）：2243－2264.

Ichinose A G，Anderson J G，Smith K D，Zeng Y.2003.Source parameters of eastern California and western Nevada earthquakes from regional moment tensor inversion［J］.Bull Seism Soc Amer，93（1）：61－84.

Kagan Y Y.1991.3－D rotation of double－couple earthquake sources［J］.Geophys J Int，106（3）：709－716.

Kagan Y Y.2007.Simplified algorithms for calculating double－couple rotation［J］.Geophys J Int，171（1）：411－418.

Kao H，Jian P R.2001.Seismogenic patterns in the Taiwan region：Insights from source parameter inversion of BATS data［J］.Tectonophysics，333（1）：179－198.

Kawakatsu H.1995.Automated near－realtime CMT inversion［J］.Geophys Res Lett，22（19）：2569－2572.

Kennett B.1983.Seismic Wave Propagation in Stratified Media［M］.Cambridge：Cambridge University Press：1－339.

Kikuchi M，Kanamori H.1991.Inversion of complex body waves－Ⅲ［J］.Bull Seism Soc Amer，81（6）：2335－2350.

Kim K H，Chiu J M，Jose P，Chen K C，Huang B S，Yeh Y H，Shen P.2005.Three－dimensional VP and VS structural models associated with the active subduction and collision tectonics in the Taiwan region［J］.Geophys J Int，162（1）：204－220.

Kubo A，Fukuyama E，Kawai H，Nonomura K.2002.NIED seismic moment tensor catalogue for regional earthquakes around Japan：quality test and application［J］.Tectonophysics，356（1－3）：23－48.

Langston C A.1981.Source inversion of seismic waveforms：The Koyna，India，earthquakes of 13September 1967［J］.Bull Seism Soc Amer，71（1）：1－24.

Ma K F，Wang J H，Zhao D.1996.Three－dimensional seismic velocity structure of the crust and uppermost mantle beneath Taiwan［J］.J Phys Earth，44（2）：85－105.

Nábělek J，Xia G Y.1995.Moment tensor analysis using regional data：Application to the 25March，1993，Scotts Mills，Oregon，earthquake［J］.Geophys Res Lett，22（1）：13－16.

Okal E A.2005.A re－evaluation of the great Aleutian and Chilean earthquakes of 1906August 17［J］.Geophys J Int，161（2）：268－282.

Pasyanos M E，Dreger D S，Romanowicz B.1996.Toward real－time estimation of regional moment tensors［J］.Bull Seism Soc Amer，86（5）：1255－1269.

Patton H，Zandt V.1991.Seismic moment tensors of western U S earthquakes and implications for the tectonic stress field［J］.J Geophys Res，96（B11）：18245－18259.

Pondrelli S，Ekström G，Morelli A，Gasperini P，Vannucci G.2006.The Italian CMT dataset from 1977to the present［J］.Phys Earth Planet Inter，159（3－4）：286－303.

Randall G E，Ammon C J，Owens T J.1995.Moment tensor estimation using regional seismograms from a Tibetan Plat－eau portable network deployment［J］.Geophys Res Lett，22（13）：1665－1668.

Rau R J，Wu F T.1995.Tomographic imaging of lithospheric structures under Taiwan［J］.Earth Planet Sci Lett，133（3－4）：517－532.

Ritsema J，Lay T.1993.Rapid source mechanism determination of large（MW≥5）earthquakes in the western United States［J］.Geophys Res Lett，20（5）：1611－1614.

Ritsema J，Lay T.1995.Long－period regional wave moment tensor inversion for earthquakes in the western United States［J］.J Geophys Res，100（B6）：9853－9864.

Romanowicz B，Dreger D，Pasyanos M，Uhrhammer R.1993.Monitoring of strain release in central and northern California using broadband data［J］.Geophys Res Lett，20（15）：1643－1646.

Scognamiglio L，Tinti E，Michelini A.2009.Real－time determination of seismic moment tensor for the Italian region［J］.Bull Seism Soc Amer，99（4）：2223－2242.

Sipkin S A.1982.Estimation of earthquake source parameters by the inversion of waveform data：synthetic waveforms［J］.Phys Earth Planet Inter，30（2－3）：242－259.

Sipkin S A，Needham R E.1989.Moment－tensor solutions estimated using optimal filter theory：global seismicity，1984—1987［J］.Phys Earth Planet Interi，57（3－4）：233－259.

Thio H K，Kanamori H.1995.Moment tensor inversion for local earthquakes using surface waves recorded a TERRAscope［J］.Bull Seism Soc Amer，85（4）：1021－1038.

Walter W R.1993.Source parameters of the June 29，1992Little Skull Mountain earthquake from complete regional waveforms at a single station［J］.Geophys Res Lett，20（5）：403－406.

Zahradnik J，Jansky J，Plicka V.2008.Detailed waveform inversion for moment tensors ofM～4events：examples from the Corinth Gulf，Greece［J］.Bull Seism Soc Amer，98（6）：2756－2771.

Stability of sparse station data inversion for deviatoric moment tensor solution of regional earthquakes

Zheng Jianchang1，2），Chen Yun－tai1）
1）Institute of Geophysics，China Earthquake Administration，Beijing100081，China
2）Earthquake Administration of Shandong Province，Jinan250014，China

Observations from regional seismic network are used in studying deviatoric moment tensor for theMW5.4earthquake of 26Febuary 2010in Taiwan adjacent area.The smallest rotation angle defined by Kagan（1991）between our result and the Havard GCMT solution is 9.5°，and the focal depth we determined is 41km，which is close to USGS location result and possibly closer to the real source.The paper also discusses the effect of station distribution on deviatoric moment tensor inversion by selecting different station combinations.The result shows that，for the data sets from three 3－component stations，the solutions are mostly accurate.The better station coverage，the less departure from real solutions.In appropriate case，the data set from two 3－components stations may result in relatively reliable solution.

deviatoric moment tensor；sparse network；discrete wave－number method；waveform inversion

10.3969／j.issn.0253－3782.2012.01.003

P315.3＋3

A

郑建常，陈运泰.2012.稀疏台网反演区域地震偏量矩张量解的稳定性.地震学报，34（1）：31－43.

Zheng Jianchang，Chen Yun－tai.2012.Stability of sparse station data inversion for deviatoric moment tensor solution of regional earthquakes.Acta Seismologica Sinica，34（1）：31－43.

中国地震局地震行业科研专项（200808068）与中国地震局监测预报司震情跟踪定向工作任务（201002220102），及山东省地震局重点科研项目（JJ1103y）和博士基金项目（10B05）联合资助.

2011－01－14收到初稿，2011－04－18决定采用修改稿.

e－mail：zjcmail＠yeah.net