小型无人机在简化传感器配置下的自主回收控制系统设计

王航宇

西安航空职业技术学院电子工程系，西安710089

小型无人机受体积和价格成本的约束，所搭载的传感器都是一些质量轻、体积小的微型器件。这些器件的精度一般都比较低，而且运行不稳定，容易随温度等因素的变化而发生变化。另一方面，如何安全精确的实现小型无人机的回收一直是小型无人机飞行控制研究中的一个重要内容。就回收方式而言，伞降回收虽然容易进行控制，但很难精确的控制着陆点，相比较而言，采用轮式起降的小型无人机的回收控制器结构虽然比较复杂，但是控制回收着陆的精确性却比较高。

基于单GPS 的小型无人机飞行控制方法，在国内外都有一定程度的研究，也有一定的工程应用基础。本文在这些研究基础之上，提出了一种仅利用单GPS 外加高度传感器组成的简易传感器组合，并基于该组合设计了一个小型无人机的自主回收控制系统。

1 回收段飞行轨迹分析

回收段是无人机飞行过程中的最后一个阶段，也是较难控制的一个阶段，这一阶段的控制任务主要体现在纵向轨迹控制方面。不失一般性，本文将无人机的回收过程分为进场、下滑、拉平和滑跑4个阶段［1］。下面分别对每个阶段进行分析、说明。

1)进场段

初始进场段，无人机从巡航高度开始，下降到指定高度并在该高度保持定高飞行。该段的控制主要表现为纵向的高度保持和横侧向的侧向偏离控制。

2)下滑段

当无人机满足下滑条件后，即从进场段转入到下滑段。在这一阶段，无人机以某给定的航迹角下滑。该段的控制主要表现为纵向的轨迹追踪和横侧向的侧向偏离控制。

3)拉平段

由于下滑过程中无人机的垂直速度过大，因此需要通过设计拉平段来减小无人机的着地速度，一般将该速度限定在－0.5m/s 到－0.6m/s 之间。常见的控制方式有轨迹控制和垂直速度控制两种。本文通过对垂直速度的控制进而使飞机沿设定的拉平航迹飞行，最终实现拉平段的控制。

4)滑跑段

当无人机按照预定的飞行轨迹将高度和垂直速度减小到接地允许的范围后，无人机就进入接地滑跑段。在进入滑跑段后，发动机关闭。利用轮子刹车系统减小滑跑速度，最终将无人机的速度降为0。这一阶段的控制主要表现为纵向的减速控制和横侧向的纠偏控制。

图1 为无人机回收过程中的纵向剖面图。

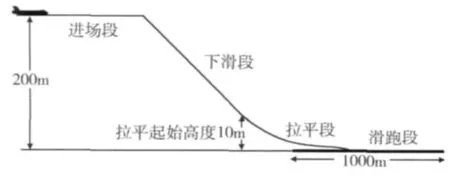
图1 无人机自主着陆全过程

2 基于单GPS 的飞行控制

GPS 不但提供了载体的速度和位置信息，而且还可以用这些信息来估计载体运动过程中的姿态信息。自从这一想法提出至今，大部分的研究工作都是围绕着如何利用多个GPS 估计载体姿态的问题展开的。

1998年，Kornfeld 给出了一个利用单GPS 测量飞行器姿态的有效算法［2］。图2 为该算法的简单计算过程。

图2 单GPS 姿态求解示意图

Kornfeld 算法的核心是利用GPS 输出的速度信息合成出飞行器的姿态信息，合成的姿态包括根据飞行器速度向量轴确定的水平航迹角、垂直航迹角和滚转角。由于速度轴不可能总是与机体轴保持一致，因此，利用该法估计出的姿态也称为“伪姿态”。按照Kornfeld 的方法，式(1)～(5)给出了相应的伪姿态计算公式。

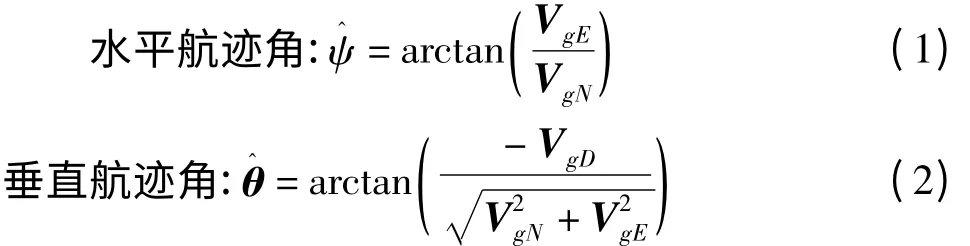
滚转角的求解需要按照如下方式进行。

在上面各式中，Vg=［VgNVgEVgD］T，Ag=［AgNAgEAgD］T，g=［0 0 gD］T。而和分别表示Ag沿着Vg的切线方向和法线方向的分量;同理，gt和gn则分别表示g 沿着Vg的切线方向和法线方向的分量。由于没有加速度计，这里的Ag是通过对Vg进行微分计算得到的。式(6)～(8)给出了伪姿态对应的角速率计算公式。

在随后的研究工作中，Sungmin Park 和Changdon Kee 对Kornfeld 的方法进行了改进，他们将GPS的星历信息和飞行器动力学方程引入到了伪姿态的求解过程中，取得了比较好的结果［3］。Sungmin Park 和Changdon Kee 提出了使用“动力学滤波器”作为外部滤波器，在姿态合成之后对合成的姿态进行滤波处理，进而得到较为理想的姿态信息。这个所谓的“动力学滤波器”其实就是系统的动力学方程。它的形式类似于卡尔曼滤波器，时域的表示形式为:

量测模型:z = h (x，u，t)+ v，其中，z =［uzpzqzrzψzθzφz］T，h(x，u，t)是量测方程，v 是量测噪声模型。

图3 给出了经过Sungmin Park 和Changdon Kee改进后的姿态确定系统的结构图。

图3 优化姿态确定系统结构图

受到研究条件的限制，本文没有将GPS 的星历信息引入到系统当中，因此也就没有图3 虚线框中的内容。姿态角的求解是按式(1)～(8)的计算过程进行解算。在姿态合成完之后，利用“动力学滤波器”对所求解的姿态角等信息进行滤波处理，从而得到与真实姿态角接近的伪姿态角。

3 自主着陆控制器结构设计

从整个回收过程来看，针对小型无人机的控制主要为纵向的高度保持，轨迹追踪，垂直速度控制;而横侧向则主要表现为侧向偏离控制。下面将对第一节论述的回收过程的4个阶段分别进行控制器结构的设计。

1)进场阶段:在进场阶段，对飞行器的控制主要表现为纵向的高度保持和横侧向的侧向偏离控制。所设计的纵向高度保持回路控制器结构如图4所示。

图4 高度保持回路控制器结构

图4 中的内回路为俯仰角保持回路，其中反馈回来的俯仰角和俯仰角速率均采用伪姿态计算式(2)和式(6)。外回路为高度保持回路，高度反馈量由高度表实时测量得到，高度给定量是预先设定的。

为保证在进场过程中，飞行器能够及时与跑道中心线对齐，因此需通过侧向偏离控制使得飞行器尽早保持在跑道中心线所在的垂直面内。图5 给出了横侧向的侧向偏离控制器结构。侧偏距和实时航向角按照给定的导航计算公式求得，而反馈量则是按照式(1)、式(5)、式(7)和式(8)计算求得。内回路为滚转保持回路，外回路为侧向偏离控制回路。

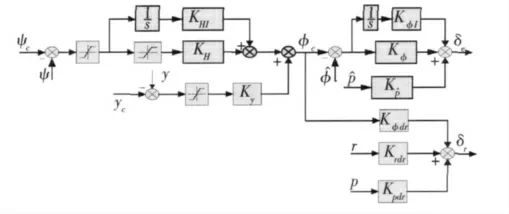
图5 侧向偏离控制器结构图

2)下滑阶段:下滑段纵向为轨迹追踪控制，横侧向为侧向偏离控制。对于纵向轨迹追踪，除了要进行高度的控制之外，还要进行垂直速度的控制。所设计的纵向轨迹追踪控制器的结构如图6 所示。其中，高度给定值是通过对预先设定的航线值进行采样得到，高度反馈值由高度传感器输出。垂直速度由GPS 提供。横侧向依然保持侧向偏离控制，其控制器结构和图5 所示的控制器结构相同。

图6 纵向轨迹追踪控制器结构图

3)拉平阶段:当飞行器距离机场高度10m 时，转入到拉平轨迹控制。拉平轨迹根据飞行器的自身性能预先设定。拉平阶段的纵向控制主要表现为垂直速度控制，控制器结构如图7 所示。横侧向依旧是侧向偏离控制，控制器结构如图5 所示。

图7 纵向拉平轨迹控制器结构

4)滑跑阶段:当飞行器结束拉平段飞行后，控制逻辑自动将控制任务转入滑跑控制阶段。在这一阶段中，纵向控制系统的主要任务就是减小飞行器的滑行速度，直到速度为0。控制器结构如图8 所示。

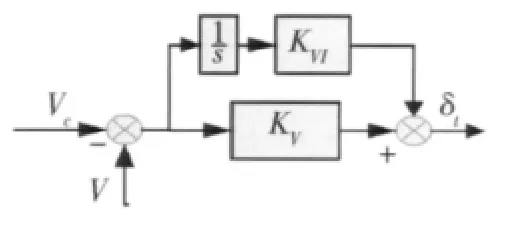
图8 纵向滑跑控制器结构

横侧向的控制任务依旧是侧向偏离控制。由于本文所研究的小型无人机体积小，速度低，因此，在滑跑过程中没有对前轮进行转弯控制。

4 控制律参数选择

在选择控制律参数时采用了序列二次规划(SQP)算法，下面对这一过程进行简单论述。

4.1 序列二次规划(SQP)算法描述

有关SQP 方法的描述如下:对于式(9)所示的二次规划问题，要求该式的解，其实就是对Langranre 函数的二次近似求解问题。

式(9)是假设约束条件为不等式约束后简化得到的，因此要得到二次求解问题则必须通过线性化非线性约束条件:

其中，▽表示梯度，矩阵Hk是Langrange 函数Hessian 矩阵的正定近似，Hk可以用任何逆牛顿方法得到更新。而上式则可以利用QP 算法来求解。

MATLAB 中的优化工具箱提供了有关SQP 算法的相关内容，下面以高度保持回路为例论述利用SQP 算法确定控制律参数的过程。

4.2 SQP 算法实现

高度保持回路的控制器结构如图4 所示。将俯仰角保持回路看作内回路。高度保持回路控制器采用PI 调节器，控制律参数分别为KH和KHi。

首先，初始化控制器参数，只要保证系统稳定就行。初始化高度保持回路的控制器参数为:KH=2，KHi=0。其次，结合飞行器自身性能确定约束条件。对本文所研究的小型无人机的高度保持回路，要求在高度差50m 时，能够在15s 内达到稳态并且控制在正负1m 的精度范围内。同时要求俯仰角速率不能大于20(°)/s。根据上面的要求在信号约束模块中添加约束条件。接着，在信号约束模块中选择调节器参数。最后，调用SQP 算法进行仿真。如果无解，则需要另行选择初始化参数，也可以适当将约束条件放宽，再重复上面的过程，直到选出理想的控制律参数。

5 数字仿真验证

在设计完控制器结构之后，利用在Simulink 环境下建立的全系统非线性仿真模型，对所设计的控制器结构和控制律参数进行数字仿真验证。

假设初始条件为:飞行高度100m，距离下滑航线中心线500m，飞行速度为该无人机的巡航速度20m/s，则该小型无人机回收过程的飞行航迹如图9所示。图10 给出了该回收过程中3个姿态角的变化曲线。

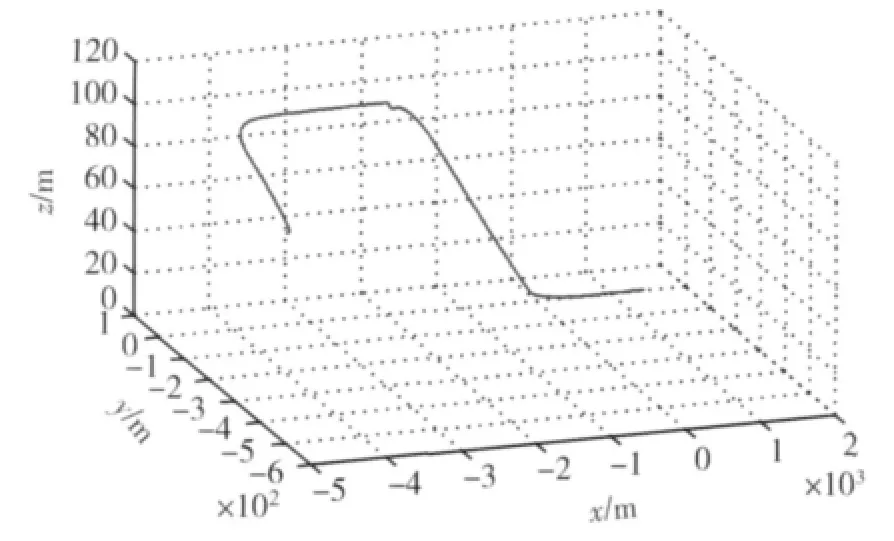
图9 小型无人机回收过程高度变化曲线

图10 回收过程中3个姿态角变化曲线

从上面的仿真结果可以看出，本文所设计的基于GPS 和高度传感器这一简化传感器组合能够实现小型无人机的自主回收控制任务。从应用的角度来看，本文所研究的自主回收系统既可以单独完成小型无人机的回收任务又可以做为常规回收系统的备份，保障小型无人机回收任务的顺利完成。

［1］张明廉.飞行控制系统［M］. 北京:航空工业出版社，2003.

［2］Kornfeld R Hansman. Single-antenna GPS Based Aircraft Attitude Determination［J］. Journal of the Insistute of Navigation，2006，45(6):51-60.

［3］Sungmin Park，Changdon Kee. Enhanced Method for Single-antenna GPS-based Attitude Determination［J］. Aircraft Engineering and Aero-space Technology:An International Journal，2006，37(8):236-243.

［4］金长江，范立钦. 飞行动力学(飞机飞行性能计算)［M］.北京:国防工业出版社，2000.

［5］Max Baarspul.A Review of Flight Simulation Techniques［J］. Progress in the Aerospace Sciences，1990，27(1):37-43.

［6］段松云. 无人机起飞/着陆阶段建模和飞行动力学仿真系统设计［D］.清华大学，2004.

［7］张江平.飞控系统中传感器的建模与仿真［D］.北京航空航天大学，2000.

［8］楼顺天，于卫.基于MATLAB 的系统分析与设计［M］.西安电子科技大学出社，2006.

［9］王伟. 无人机自动着陆控制系统的设计与实现研究［D］.西北工业大学，2006.