基于ABAQUS的内河航道岸坡稳定性分析

程 曦 ，王元战 ，马殿光，肖 忠，郝林南

（1.天津大学建筑工程学院天津市港口与海洋工程重点实验室，天津300072；2.交通运输部天津水运工程科学研究所工程泥沙交通行业重点实验室，天津300456）

河道土质岸坡失稳破坏是一种几乎存在于世界上所有江河岸坡的现象。河流上建设枢纽后，航道两岸塌岸更为严重。航道岸坡失稳引起沿岸地带的建筑物破坏，造成财产损失；同时，岸坡失稳将侵蚀两岸土地资源，危害航道通航条件，也极大增加了航道的维护费用。因此，开展航道护岸稳定的研究具有十分重要的意义。

影响航道岸坡稳定性的因素很多，包括渗流、降雨、波浪力等，本文主要研究稳定渗流和波浪力对岸坡的影响。在渗流方面，陈丽刚［1］基于ABAQUS对边坡稳定渗流进行了流固耦合分析。张晓咏［2］应用ABAQUS对坝体的渗流进行了研究，并验证了强度折减法的可靠性。周群华、章广成等［3-4］研究了水位变化对边坡稳定性的影响。在船行波方面，项菁等［5-7］对船行波波要素的特点以及现有的一些计算公式进行了总结和分析。卢无疆［8］对高速双体客船和普通船的船行波进行了现场观测，得到了各种波浪要素。简文彬［9］对边坡对循环荷载的响应进行了研究。

虽然不少学者已经对边坡失稳的影响因素进行了研究，但都只是针对单一影响因素研究，缺乏对多种因素共同作用下边坡失稳的研究，实际上边坡失稳是多种因素共同作用下的结果，因此多因素共同作用下边坡的稳定性研究也是必不可少的。本文除了分别分析稳定渗流和波浪力这2个影响因素之外，还将其组合起来，研究这2种因素共同作用对边坡稳定性的影响。

本文采用大型有限元分析软件ABAQUS，通过数值模拟对岸坡进行流固耦合分析，并采用强度折减法分析岸坡的稳定性。在单独考虑渗流时，先计算不同静水位下边坡的安全系数，然后在数值模型上施加不同的水头差，计算稳定渗流情况下的安全系数，最后与极限平衡方法的计算结果相对比。在单独考虑波浪力时，参考实测的波浪要素，根据规范计算出波压力的分布，并在模型上施加周期荷载，研究不同波高、周期的船行波对边坡稳定的影响。在考虑共同作用时，将之前计算的工况组合起来，研究2种因素共同作用下对岸坡稳定性的影响，并与单因素的计算结果进行对比分析。

1 基本原理

1.1 ABAQUS流固耦合分析的基本原理

ABAQUS可对多孔介质的渗流和变形进行耦合分析，可进行非饱和土的渗流计算。ABAQUS中处理孔隙介质中的流体流动的方式是将孔隙体视为多相材料，孔隙中的流体可包含两部分：一是液体，通常认为压缩性相对很低；另一个则是气体，认为是可压缩的。土体的体积包括两部分：土颗粒的体积和孔隙的体积，孔隙的体积等于孔隙中液体的体积与气体体积之和。计算中有限元的网格固定在土骨架上，气体或液体可流过网格，但需要满足流体的连续性方程。土体的力学特性通过采用有效应力定义的本构模型来模拟，液体的渗透采用Forchheimer渗透定律模拟，常用的Darcy定律是它的简化。

式中：δv为虚速度场；δε=sym（∂δv/δx）为虚应变；σ 为真实（Cauchy）应力；t为单位面积上的表面力；为单位体积上的体积力。

渗流连续方程为

式中：vw为流体的平均流速；n为边界S的外法线；该方程对ρw0进行了归一化。Forchheimer渗透定律表达式为

ABAQUS能将渗流场和应力场直接藕合，无需进行渗流场和应力场的反复迭代，只要按时间过程连续求解就可得到全部结果，即通过将节点位移和孔隙水压力作为节点自由度进行空间离散，将应力平衡方程和渗流连续方程写成矩阵形式，并对渗流连续方程引入时间积分，得到耦合控制方程，然后在每个时间步内求解方程，并同时满足位移边界条件和渗流边界条件。

1.2 有限元强度折减法基本原理

边坡稳定的分析方法主要可分为两大类：第一类可称作传统方法，如极限平衡法、极限分析法、滑移线法等；第二类为基于计算机技术的数值分析方法，如有限元法、离散元法、边界元法等［10］。对于稳定渗流的土坡稳定分析，传统的极限平衡条分法分成2种方法［11］：一种是根据边界孔隙水压力和饱和的重度考虑渗流作用的常用方法；另一种是根据渗透力和浮重力考虑渗透作用的分析方法。前者需要绘制流网求得孔隙水压力，而后者由于计算渗透力很不方便，工作量较大，在工程实践中较少采用。本文采用的有限元强度折减法，能够很好地克服极限平衡法的缺点，因而已经被广泛的应用到了有数值分析中。

抗剪强度折减系数（SSRF：Shear Strength Reduction Factor）的概念是由Zienkiewicz等1975年在《土工弹塑性有限元数值分析》一文中首次提出的，其定义为：在外载荷保持不变的情况下，边坡内土体所能提供的最大抗剪强度与外载荷在边坡内所产生的实际剪应力之比。在极限状况下，外载荷所产生的实际剪应力与抵御外载荷所发挥的最低抗剪强度（即按照实际强度指标折减后所确定的、实际中得以发挥的抗剪强度）相等。当假定边坡内所有土体抗剪强度的发挥程度相同时，这种抗剪强度折减系数相当于传统意义上的边坡整体稳定安全系数Fs，又称为强度储备安全系数，与极限平衡法中所给出的稳定安全系数在概念上是一致的。

折减后的抗剪强度参数表达式为

式中：c、φ为土体所能够提供的抗剪强度；cm和φm为维持平衡所需要的或土体实际发挥的抗剪强度；Fs为强度折减系数。

判断岸坡是否达到临界破坏的标准主要有以下几种［12］：（1）以数值计算收敛与否为评价标准，与有限元的算法有关；（2）以特征点的位移-折减系数曲线的拐点为评价标准；（3）以是否形成连续塑性变形贯通区为评价标准。

本文采用以是否形成连续塑性变形贯通区作为评价标准。

1.3 摩尔库仑（Mohr-Coulomb）模型及参数的选取

为与传统极限平衡法对边坡岩土体进行刚塑性（理想塑性）假设相对应，本文采用的本构模型是Mohr-Coulomb准则。为避免经典Mohr-Coulomb准则在三维主应力空间和π平面上，屈服面存在棱边和尖角（奇点），导致塑性流动方向不唯一、数值计算繁琐和收敛缓慢的问题，ABAQUS软件采用的是Mohr-Coulomb屈服准则的扩展。其采用Mohr-Coulomb屈服函数，包括粘聚力的各向同性硬化和软化，但该模型的流动势函数在子午面上的形状为双曲线，在π平面上没有尖角，因此势函数完全光滑，确保了塑性流动方向的唯一性。

数值模型中需要输入的主要参数分别是：弹性模量E、泊松比 v、内摩擦角 φ′、粘聚力 c′、剪胀角 Ψ、饱和土的渗透系数k。除此之外还要考虑浸润面以上的非饱和土中的渗流，计算中还需输入非饱和土的土水特征曲线。其中为保守考虑剪胀角取值Ψ=0°，其他参数都由通过三轴固结不排水剪（测孔隙水压力）试验确定。土样为饱和粘土，取自广西壮族自治区右江上游那吉库区段。

在考虑波浪的动荷载作用时，本文主要从粘土在循环荷载作用下抗剪强度降低这方面考虑，通过动三轴试验，分别测出动应力与偏应力之比S1=σd1/（σ1-σ3）=0.1、S2=σd2/（σ1-σ3）=0.2时土体的抗剪强度。不同动应力与偏应力之比下土体参数如表1所示。

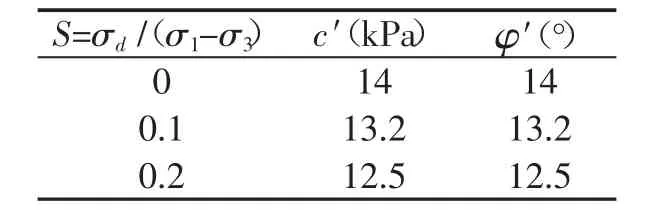
表1 不同动应力与偏应力之比下土体参数Tab.1 Soil parameter with different strength weakening factors

图1 岸坡尺寸Fig.1 Slope dimension

2 计算实例

2.1 边坡稳定渗流分析

根据广西那吉库区地形图可知当地为均质岸坡，坡高8 m，坡比为1：3，航道正常水位为5 m。根据三轴固结不排水试验可知有效内摩擦角 φ′=14°，有效粘聚力 c′=14 kPa，重度r=18 kN/m3，弹性模量 E=20 MPa，泊松比 v=0.4，渗透系数k=10-8m/s，岸坡尺寸如图1所示。

有限元模型采用孔压/位移耦合的CPE8R四边形八节点平面应变单元，共含有870个单元、2 757个节点。上部边界为自由边界，边坡底面采用完全约束条件，左右采用水平约束条件。受力为重力和静水压力。网格划分如图2所示。

（1）算例一。计算不同静水位下边坡的安全系数，水位分别为4 m、5 m、6 m。

首先在不同静水位条件下使用Geostatic分析步平衡地应力，然后在Soil分析步中选择稳态分析采用强度折减法计算安全系数，并与Morgenstern-Price法计算结果进行对比（表2）。

图2 网格划分Fig.2 Calculation model

表2 不同静水位下的安全系数Tab.2 Safety factors of slopes under different still water levels

由表2可知，静水位下安全系数随着静水位的上升而增大，有限元强度折减法计算的安全系数与Morgenstern-Price法的误差最大为3.52%，在合理范围内。

（2）算例二。计算不同水位稳定渗流情况下的岸坡稳定性，水头差分别为1 m、2 m、3 m。

首先使用Geostatic分析步平衡不同水位时的地应力，然后在Soil分析步中选择稳态分析，并改变边界的孔压条件以达到稳定渗流，最后采用Soil分析步中的稳态分析进行强度折减以获得该边坡稳定的安全系数，强度折减系数Fs=1.0时为边坡初始状态。

航道正常水位为5 m，在不同地下水位的工况下岸坡稳定渗流的安全系数计算结果如表3所示。

水头差与安全系数关系曲线如图3所示。

由表3和图3可以看出，随着水头差的增大边坡安全系数呈现线性减小趋势，有限元强度折减法计算的安全系数与Morgenstern-Price法的误差最大为2.19%，在合理范围内。

对比有限元强度折减法计算的安全系数与Morgenstern-Price法的计算结果，可以从表2和表3中看出最大的误差仅为3.52%，这体现出有限元法与传统极限平衡法的计算结果有较好的一致性，也说明将塑性区贯通作为失稳判据确定边坡稳定安全系数是可行的，也是合理的。

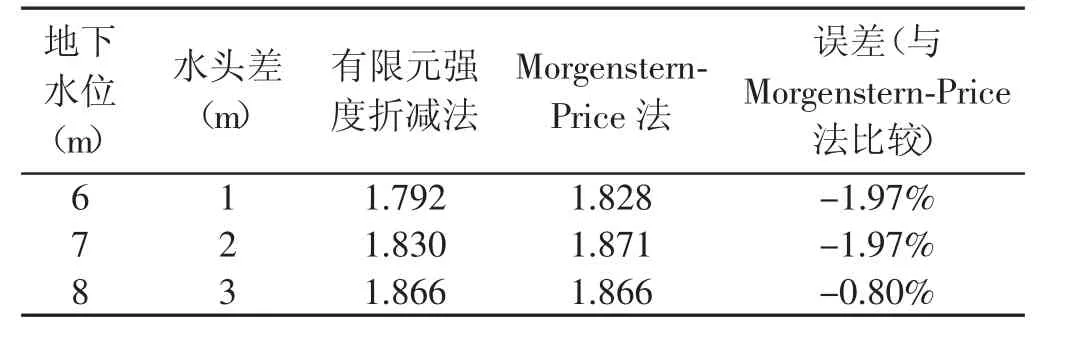
表3 稳定渗流下的安全系数Tab.3 Safety factors of slopes under steady seepage

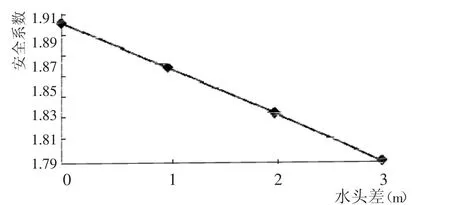
图3 水头差与安全系数关系曲线Fig.3 Curve between head differences and safety factors

2.2 波浪对边坡稳定影响分析

算例三：计算不同波浪力作用下岸坡的稳定性，此时水位为正常静水位5 m。

根据卢无疆［8］对高速双体客船和普通船的船行波的现场观测结果，2种船型波各选一组波浪要素进行分析。

（1）高速双体客船：Vma=13.11 m/s，Hmaxa=0.45 m，=2.5 s，作用时间。

（2）普通船：Vmb=6.25 m/s，Hmaxb=0.28 m，=1.8 s，作用时间。

根据海港水文规范（JTJ 213-98）8.1.4.2，波峰时，静水面处波压力 Psa=γHmaxa=4 500 Pa，Psb=γHmaxb=2 800 Pa，并将波浪力按照波峰时的分布简化为正弦波。波峰时波压力分布如图4所示。

首先使用Geostatic分析步平衡正常水位不同土体强度下的地应力，然后采用Soil分析步中的稳态分析进行强度折减，最后采用Soil分析步中的瞬态分析，并加上不同的波浪力循环荷载。不断调节场变量的值进行计算，直到Soil分析步中的瞬态分析结束时岸坡刚好形成连续塑性变形贯通区，此时对应的场变量值即为边坡的安全系数。在船行波作用下边坡的安全系数计算结果如表4所示。

动应力与偏应力之比与安全系数关系曲线如图5所示。

图4 波压力分布示意图Fig.4 Sketch of wave pressure distribution

表4 船行波作用下的安全系数Tab.4 Safety factors of slopes under wave pressure

从表4和图5可以看出，高速双体客船对岸坡安全系数的影响要比普通船大0.015左右。波浪力在土体强度未折减时对边坡的稳定性影响不大，但是粘土在循环动荷载作用下发生强度弱化对边坡的稳定性有较大影响，随着弱化程度的加剧，边坡的安全系数基本呈线性减小的趋势。

2.3 稳定渗流和波浪共同作用下边坡稳定影响分析

算例四：选取稳定渗流水头差为3 m的工况与船行波的各种工况组合进行分析。

首先使用Geostatic分析步平衡正常水位不同土体强度下的地应力，然后采用Soil分析步中的稳态分析进行强度折减，再采用Soil分析步中选择稳态分析，并改变边界的孔压条件以达到稳定渗流，最后采用Soil分析步中的瞬态分析，并加上不同的波浪力循环荷载。不断调节场变量的值进行计算，直到Soil分析步中的瞬态分析结束时岸坡刚好形成连续塑性变形贯通区，此时对应的场变量值即为边坡的安全系数。计算结果如表5所示。

动应力与偏应力之比与安全系数关系曲线如图6所示。

从表5和图6可以看出，高速双体客船和普通船船行波作用下的岸坡安全系数之间的差别较小，渗流和波浪力的共同作用对岸坡的稳定性已有较大影响，在土体强度未弱化时，边坡的安全系数的降幅达到0.12以上。粘土在循环动荷载作用下发生强度弱化时，随着弱化程度的加剧，边坡的安全系数也是基本呈线性减小的趋势。

有无稳定渗流下边坡的安全系数对比结果如图7所示。

由图7可以看出，土体强度的弱化对岸坡稳定会产生较大影响，最大差值达到0.223。无论是在有无渗流的作用下，粘土在循环动荷载作用下发生强度弱化时，随着弱化程度的加剧，边坡的安全系数减小的趋势是相同的，基本为线性分布，且相互平行。由此可见考虑土体强度弱化时，稳定渗流和波浪力这2个影响因素是相互独立的。

图5 动应力与偏应力之比与安全系数关系曲线Fig.5 Curve between reduction factors and safety factors

表5 共同作用下的安全系数Tab.5 Safety factors of slopes under interaction

图6 动应力与偏应力之比与安全系数关系曲线Fig.6 Curve between strength weakening factors and safety factors

图7 动应力与偏应力之比与安全系数关系曲线Fig.7 Curve between strength weakening factors and safety factors

算例五：不考虑土体强度弱化，计算不同水头差稳定渗流和船行波的各种工况组合进行分析。

首先使用Geostatic分析步平衡正常水位下的地应力，然后采用Soil分析步中的稳态分析进行强度折减，再采用Soil分析步中选择稳态分析，并改变边界的孔压条件以达到不同水头差下的稳定渗流，最后采用Soil分析步中的瞬态分析，并加上不同的波浪力循环荷载。不断调节场变量的值进行计算，直到Soil分析步中的瞬态分析结束时岸坡刚好形成连续塑性变形贯通区，此时对应的场变量值即为边坡的安全系数。计算结果如表6所示。

共同作用时不同水头差下边坡的安全系数对比结果如图8所示。

由图8可以看出，不考虑土体强度弱化时，船行波对岸坡稳定性的影响最大只有0.034，在不同水头差的稳定渗流船行波对安全系数的影响基本为一定值，由此可见在不考虑土体强度弱化时，稳定渗流和波浪力这2个影响因素也可以看作是相互独立的。

表6 共同作用时不同水头差下的安全系数Tab.6 Safety factors of slopes under head differences

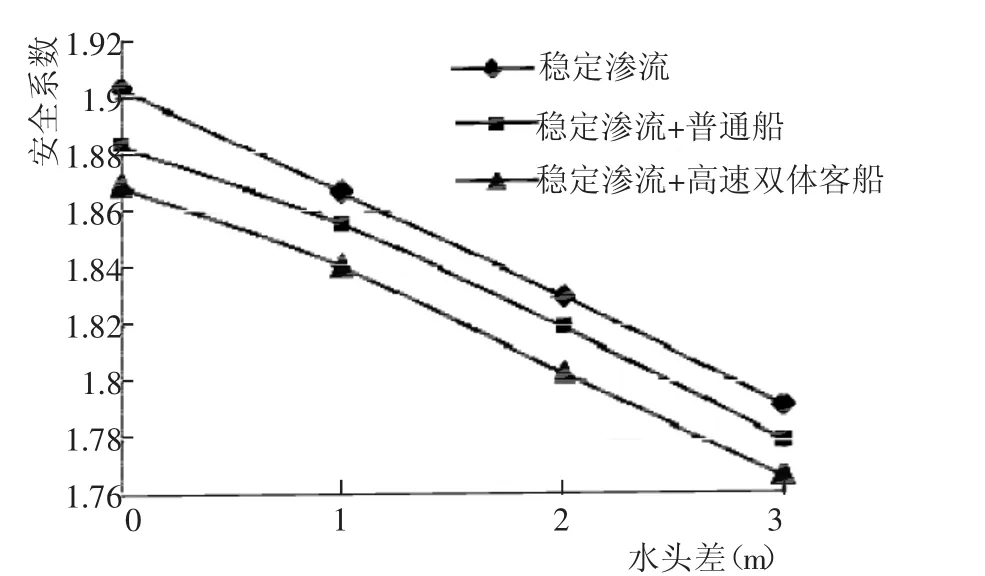
图8 水头差与安全系数关系曲线Fig.8 Curve between head differences and safety factors

3 结论

通过以上算例的计算与分析可以得到以下结论：

（1）本文采用的ABAQUS有限元强度折减法计算的安全系数与传统极限平衡Morgenstern-Price法的计算结果无论是在静水位还是稳定渗流情况下都只产生了较小误差，验证了本文采用方法的可靠性，同时也说明以是否形成连续塑性变形贯通区作为边坡破坏的评价标准是可行的。

（2）岸坡的安全系数随着水位的增长而增大。在岸坡稳定渗流时，水差越大安全系数越小。高速双体客船船行波比普通船船行波对岸坡的影响要大。粘土在循环动荷载作用下发生强度弱化会对边坡的稳定性产生较大影响。

（3）当稳定渗流和波浪力共同作用时，边坡安全系数最小，其变化趋势与无渗流的情况相同。当稳定渗流和波浪力共同作用时，2个因素之间不互相影响，可以看作是相互独立的。

本文建立的数值模型与采用的土体参数均来自广西壮族自治区右江上游那吉库区，这对当地岸坡的稳定性研究具有重要的意义，同时也为研究边坡在多因素共同作用下的稳定性提供参考。

［1］陈丽刚.基于ABAQUS渗流与应力耦合作用的边坡稳定性分析［D］.郑州：郑州大学，2010.

［2］张晓咏，戴自航.应用 ABAQU 程序进行渗流作用下边坡稳定性分析［J］.岩石力学与工程学报，2010，29（1）：2 927-2 934.ZHANG X Y，DAI Z H.Analysis of Slope Stability under Seepage by Using ABAQUS Program［J］.Chinese Journal of Rock Mechanics and Engineering，2010，29（1）：2 927-2 934.

［3］周群华，闫澍旺，邓卫东，等.水库水位变化对某岸区公路边坡稳定性影响分析［J］.公路交通科技，2011，28（6）：32-39.ZHOU Q H，YAN S W，DENG W D，et al.Analysis of Influence of Reservoir Water Level Fluctuation on Stability of a Bank Slope［J］.Journal of Highway and Transportation Research and Development，2011，28（6）：32-39.

［4］章广成.水位变化对滑坡稳定性的影响研究［D］.武汉：中国地质大学，2005.

［5］项菁，石根娣.天然航道船行波波高计算方法［J］.河海大学学报，1994，22（2）：47-48.XIANG J，SHI G D.Calculation of Ship Wave Heights in Navigable Channels［J］.Journal of Hohai University，1994，22（2）：47-48.

［6］张璠，张绪进，尹崇清.船行波与运河岸坡的研究综述［J］.中国水运：学术版，2006，6（5）：45-50.ZHANG F，ZHANG X J，YIN C Q.Research Summary of Ship Wave and Canal Slope［J］.China Water Transport：Academic Version，2006，6（5）：45-50.

［7］潘宝雄，蒋宗燕.船行波问题的研究综述［J］.河港工程，2001（1）：14-19.PAN B X，JIANG Z Y.Research Summary of Ship Wave［J］.River Port Engineering，2001（1）：14-19.

［8］卢无疆.高速双体客船船行波特性现场观测［J］.水利水运科学研究，1995（2）：191-196.LU W J.On Prototype Observation of Ship Wave Characteristics of High-speed Double Volume Ship［J］.Hydro-Science and Engineering，1995（2）：191-196.

［9］简文彬，胡忠志，樊秀峰，等.边坡对循环荷载的响应研究［J］.岩石力学与工程学报，2008，27（12）：2 563-2 567.JIAN W B，HU Z Z，FAN X F，et al.Research on Responses of Slope Under Cyclic Load［J］.Chinese Journal of Rock Mechanics and Engineering，2008，27（12）：2 563-2 567.

［10］Abramson L W，Lee T S，Sharma S，et al.Slope stability and stabilization methods［M］.New York：Wiley，2001.

［11］杨进良.土力学［M］.北京：中国水利水电出版社，2000.

［12］费康，张建伟.ABAQUS在岩土工程中的应用［M］.北京：中国水利水电出版社，2009.