圆面积上作用垂直荷载下横观各向同性地基的统一解

高雪冰，顿志林

（1.黄山学院 建筑工程学院，安徽 黄山245041；2.河南理工大学 土木工程学院，河南 焦作454000）

0 引 言

目前，在地基基础工程设计中，应用最广泛的是Winkler模型和弹性半空间地基模型，但实际地基并不是均质各向同性、理想的半无限体。由于各种原因，天然地基在形成过程中一般都具有固有的横观各向同性，如在沉积过程中形成的层状结构黏性土、页岩等，不同薄层内的矿物成份及物理力学性质是不同的。 Simons，King，Selvadurai[1-3]等许多学者认为成层均匀的横观各向同性弹性半空间可以表示范围广泛的地基。其中弹性体轴对称应力分析问题在工程中有重要意义，苏联学者Lekhnitskii[4]于1940年给出了横观各向同性体轴对称问题的通解，Eubanks和Sterberg[5]从位移表示的平衡方程出发，于1954年系统地推导了Lekhnitskii解；国内胡海昌，[6]丁皓江，[7]王炜[8]等对此问题也做了大量的工作。

文献[9]已对几种常见轴对称荷载下特殊横观各向同性地基的位移和应力进行了具体的分析。本文通过对各向同性下的Love位移函数重新修正，采用位移解法的基本原理，同时利用Hankel积分变换和其反演变换和Bessel函数理论，[10]讨论了当材料特征值s1=s2=s时，圆面积上作用垂直荷载下的横观各向同性地基问题的位移和应力统一解。

1 基本方程

对于横观各向同性轴对称问题，其平衡微分方程为（不考虑体积力）：

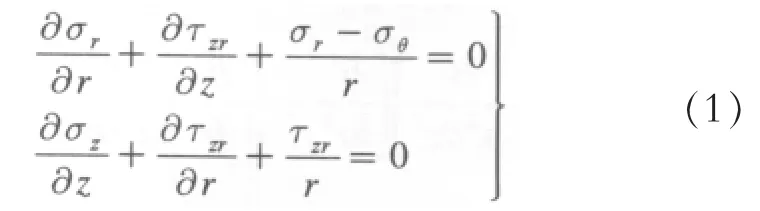
将几何方程代入横观各向同性轴对称问题的本构方程，即可得到用位移分量表示的物理方程为：

式中

4结 论

本文基于将各向异性地基视为横观各向同性地基模型，通过对各向同性下的Love位移函数进行重新修正；采用位移解法的基本原理，利用Hankel积分变换和其反演变换以及Bessel函数理论，得到了当材料特征值s1=s2=s时，圆面积上作用垂直荷载下的横观各向同性地基问题的统一解。当已知横观各向同性地基表面上作用的荷载p(r)和5个独立工程弹性参数E1、E2、μ1、μ2、G2、时，即可利用本文结论得到圆面积上作用任意垂直轴对称荷载下的横观各向同性地基的位移和应力分布情况。

[1]Simons N E，Minzies.B.K.A short course in foundation engineering[M].2nd ed， New York：Wiley，1975:51-70.

[2]King G J K.An introduction to superstruction-raft-soil interaction[M].University of Roorkee，1971:110-133.

[3]Selvadurai A P S.Elastic analysis of a soil-structure interaction[M].New Jersey:Prentice-Hall，1978:74-114.

[4]Lekhnitskii S G.Symmetric deformation and torsion of bodies of revolution with anisotropy of a special kind[J].PPM，1940，(3)43-60.

[5]Eubanks R A，Sternberg E.On the axisymmetic problem of elasticitytheory equationsfor amediawithtransversely isotropy[J].Journal of rational mechanics analysis，1954，（3）:89-101.

[6]胡海昌.横观各向同性体的弹性力学的空间问题[J].物理学报，1953，9(2):130-147.

[7]丁皓江.横观各向同性弹性力学[M].杭州:浙江大学出版社，1997:45-117.

[8]王炜，徐新生.关于横观各向同性弹性体轴对称问题的通解[J].北京大学学报，1994，31(3)，303-308.

[9]高雪冰.特殊横观各向同性地基空间问题的位移与应力分析[D].焦作:河南理工大学，2007:25-47.

[10]郭大智，马松林.路面力学中的工程数学[M].哈尔滨:哈尔滨工业大学出版社，2001:97-167.

[11]刘干斌.横观各向同性地基轴对称问题的应力和沉降分析[D].焦作:焦作工学院，2002:7-32.