耗散粒子动力学中Lees－Edwards边界条件的实施

陈 硕，金亚斌，张明焜，尚 智

（1.同济大学 航空航天与力学学院，上海200092；2.高性能计算研究所，A＊STAR，新加坡138632）

Lees－Edwards边界条件（简称LE）最初在分子动力学中模拟简单剪切流动［1］，该边界条件的特点是在不需要固体壁面拖动的情况下在准无限大流体系统中获得定常的剪切率.

基于粒子的数值模拟方法中，密集排列的粒子一般会对近壁面区域内流体密度、温度等参量有一定的影响，进而影响到流动的主体.LE 方法在边界附近的区域内则不会出现物理参数的数值反常波动.LE 边界条件其原理也适合于基于粒子的其他模拟方法，最近Lorenz等［2］，Wagner等［3］研究了LE边界条件在格子－波尔兹曼方法（简称LB）中的实施，并模拟了悬浮液的剪切流动等.

将从微观、介观到宏观不同层次及尺度的模拟联系起来正成为计算机模拟领域最富挑战性的重要课题.介观模拟更是一项为实现“第一原理预计物质宏观性质”奠定物理基础的关键技术［4］，而发展适宜的介观尺度的流体模拟技术是近年来国际计算机模拟领域的热点［5］，其特征为在分子尺度上进行粗粒化处理（即忽略最细节的分子结构），而在介观尺度上捕捉流体的物理特性.

耗散粒子动力学（简称DPD）是一门新兴的基于粒子的介观尺度数值模拟技术，于1992 年首次由Hoogerbrugge和Koelman提出［6］.尽管DPD 不如LB计算省时，但是DPD 比LB 灵活得多，尤其不会象LB那样在很多情况下出现数值不稳定性［7］.另一方面，DPD 又可以理解为宏观的微分流动控制方程在小尺度上的随机描述，从这个意义上说，DPD 方法是连接微观分子动力学方法和宏观流体力学方法的一座桥梁.

DPD 已经成功地应用于对复杂流体和复杂流动过程的模拟［8－13］，其中包括早期的DPD算法结 合LE边界条件获得简单剪切流动［6，14］.随着DPD 中计算方法的改进，在DPD 中实施LE边界条件，需要将LE条件与DPD 中所采用的velocity－Verlet算法以及元胞分割方法等结合起来考虑.本文结合上述算法详细讨论了LE条件在DPD 方法中的实施过程，并对在LE 边界条件下所获得的速度、密度、压强、剪切应力等参数的分布进行了比较分析与讨论.通过提高耗散力系数来模拟较高的Schmidt数流体，结果表明在高耗散率条件下，在耗散粒子动力学中应用Lees－Edwards边界条件仍然有效.

1 耗散粒子动力学

1.1 耗散粒子动力学理论模型

基于牛顿运动方程，DPD 系统中粒子的位置和速度随时间的变化规律为

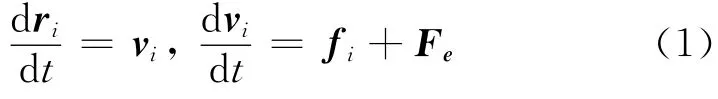
式中：ri和vi为第i个粒子的位置和速度矢量；t为时间；fi为所有其他粒子（不包括粒子i本身）作用在粒子i上的力；Fe为粒子所受到的其他外力如高分子链的弹性力等.DPD 系统中单位质量为单个粒子的质量，因此作用在每个粒子上的力的大小等于粒子的加速度值.粒子之间的动力相互作用由耗散力和随机力组成.

fi包括保守力FC，ij、耗散力FD，ij和随机力FR，ij三部分，其中每一部分都表示粒子之间的两两相互作用.

式中的求和符号对一定的截断半径rc内所有的不包括粒子i的其他粒子进行求和.如果粒子之间的距离rij＞rc，则粒子之间的相互作用为零.

保守力FC，ij为作用在2个粒子质心连线方向上的粒子之间的排斥力，可表示为

式中：aij为保守力系数，表示粒子i与粒子j间最大的排斥力值；rij＝ri－rj，rij＝｜rij｜，r＾ij＝rij／｜rij｜.粒子j作用在粒子i上的耗散力（或者阻力）FD，ij可以表达为

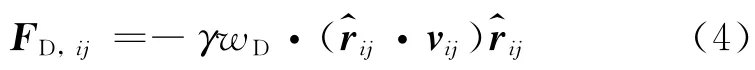
式中：γ为耗散系数；wD为与粒子间距离rij有关的权函数，当rij≥rc时，wD＝0；vij为粒子之间相对速度，vij＝vi－vj.随机力FR，ij可表达为

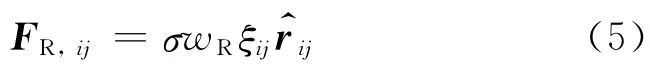
式中：σ为随机力系数；wR为与粒子之间距离rij有关的权函数，称为随机力权函数，当rij≥rc时，wR＝0；ξij为 随 机 变 量，其 平 均 值 为 零 且 方 差 为Δt－1，Δt为时间步长.与保守力一样，随机力和耗散力也作用在粒子质心的连线方向.

Español等［15］研究表明，式（4）和（5）中的2 个权函数相互关联，两者只能任取一个，其相互关系为

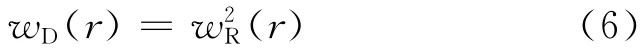
γ和σ也相互关联，两者也只能任取一个

式中：kB为Boltzmann常 数，T为 温 度，kBT为 系 统的Boltzmann温度，与系统的涨落－耗散理论相类似［16］.将kBT作为能量的单位，则有

Fan等［17］的研究表明，采用平方根的权函数有利于提高DPD 系统的Schmidt数，因此本文中采用改进的权函数表达式，即rc取单位长度，即rc＝1.

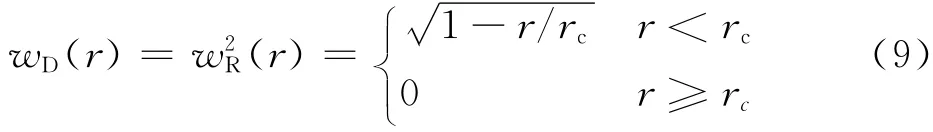
1.2 粒子间作用力的计算

在DPD 中如何恰当选取方法计算粒子间相互作用力将在很大程度上影响整个模拟所花费的时间，元胞分割法（cell subdivision）［18］不 失为一种高效的方法.如图1所示，计算区域被划分为一系列的元胞区域，每个元胞的边长均大于rc.计算区域内的各DPD 粒子处于不同的元胞区域内.显然，粒子之间的相互作用仅仅发生在处于同一个元胞内的粒子之间以及分别处于2个紧邻的元胞内的粒子之间；否则，粒子之间的相互距离必定大于rc，从而可以不考虑其相互作用.因此，在计算某个粒子与周围粒子的相互作用时，可以只计算该粒子与其属于同一个元胞内的其他粒子之间的相互作用以及该粒子与紧邻的周围元胞内的粒子的相互作用.这样的方法，避免了所求解的粒子与计算区域内的粒子之间全部求解相互作用力，可以大幅节约计算工作量.

由于粒子间相互作用力的对称性，因此可以仅考虑相邻的元胞中的一半数目，对于二维问题来说，是5个元胞（含中心元胞本身）；对于三维问题来说，是14个元胞（同样也含中心元胞本身）.对于周期性边界条件，相邻的镜像元胞也必须计算在内.这些细节，在与LE边界条件的结合中必须仔细考虑.

1.3 数值积分算法

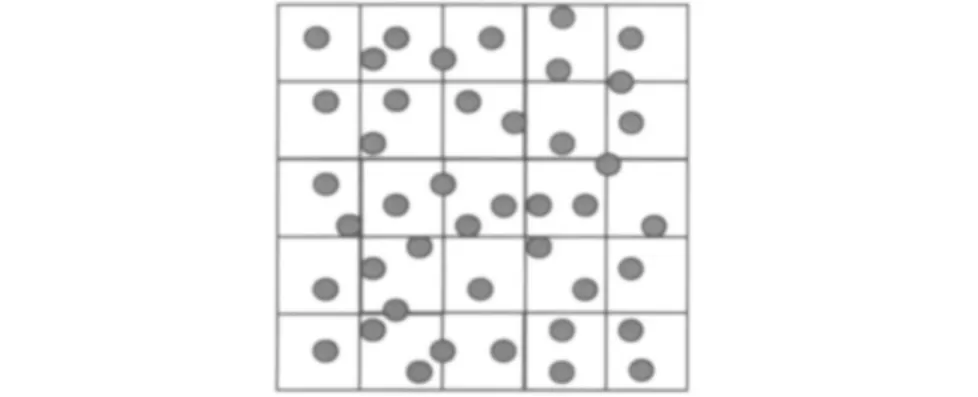
图1 元胞分割法示意Fig.1 Schematic diagram of cell subdivision method

目前DPD 中已采用改进的velocity－Verlet算法［19］来更新每个粒子在新时刻（即t＋Δt时刻）的位置、速度以及受力情况.如下所示：ri（t＋Δt）＝式中：为粒子i在t＋Δt时刻的预估速度；λc为经验系数.如果粒子的受力情况与粒子间的相对速度无关，则λc＝0.5.Groot和Warren［19］发现，DPD方法中λc的最优值为0.65.当采用该最优值同时取ρ＝3，σ＝3时，对平衡系统的模拟中计算的时间步长可以增加到Δt＝0.06而不失去对温度的控制.

2 LE边界条件与DPD中算法的结合

2.1 LE边界条件

LE 边界条件可模拟周期性的简单剪切流动［20］.图2为周期性系统中简单剪切流动示意图，图中L为周期性区域在z方向的长度，ux为x方向的流体剪切速度.假定所研究的区域内仅有2个粒子.在粒子运动的过程中，受到处于本区域内其他粒子及周期性镜像区域内粒子的作用.由于剪切率Dx＝∂ux／∂z，镜像区域各自角点的x方向速度u（r，t）与z成正比，即u（r，t）＝iDxz，其中i为x方向单位矢量.

图2 LE 边界条件示意Fig.2 Schematic diagram of LE boundary condition

在粒子运动过程中，如果粒子跑出了计算区域，该粒子将由其周期性镜像粒子代替而重新进入该计算区域.然而在剪切流动条件下，粒子穿过z＝0面或者z＝L面时，其对应的周期性镜像粒子并不会有同样的流体速度以及同样的x坐标.跑出计算区域的粒子以周期性镜像的身份再进入该区域时如果赋予特定的速度和x坐标可产生剪切流动.整个流动过程中其空间上是均匀的，不会感受到边界的存在，这是LE边界条件的优点.

具体来说，在模拟区域中，令其角点O的流体速度为零.所模拟区域中DPD 粒子的速度由两部分构成，即DPD 粒子的热速度ci和流体速度u（ri），即

简单剪切中由于流体速度是只以z为自变量的函数，这里只需要考虑在z方向上粒子穿越边界的情况.零时刻ri的镜像矢量r′i在ri＋kL处，ri的镜像矢量r″i在ri－kL处.t时间后，该粒子及镜像的位置分别为其中，ci和zi（包括其镜像）都是时间的函数.由于粒子的热速度及其所有镜像粒子的热速度都是相同的，因此，那么同理kL－iDxLt.如果ri（t）跑出了下边界，将被其镜像代替

如果ri（t）跑出了上边界，将被其镜像r″i（t）代替

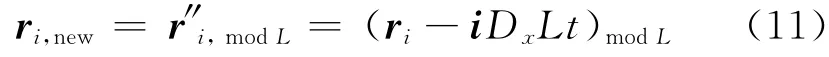
2.2 DPD中的算法与LE边界条件的结合

如图3所示，模拟区域显示x，z方向，y方向垂直纸面向里，图中的方格代表元胞.由于流动存在剪切率Dx，所以粒子离开下边界而以镜像粒子的身份从上边界被引入时x方向的速度要加上DxLz，即速率变为ux＋DxLz.由于x方向速度的差异，一定时间后在上边界被引入的x方向的位置也会相应改变Δx，也就是图形上部实线粒子与虚线粒子x方向距离差Δx＝ntVxΔt－［ntVxΔt／Lx］Lx，其中nt为时间步数，Δt为时间，［］为取整符号，Lx为模拟区域x方向的总长度.从计算区域下部跑出去的粒子将从上边界处一个新的位置进入计算区域，从而能够保证能量守恒［1］.相应地在计算粒子间相互作用时其相邻的粒子也需要更新，因此DPD 所采用的元胞分割法中的所有细节也必须与此相对应.

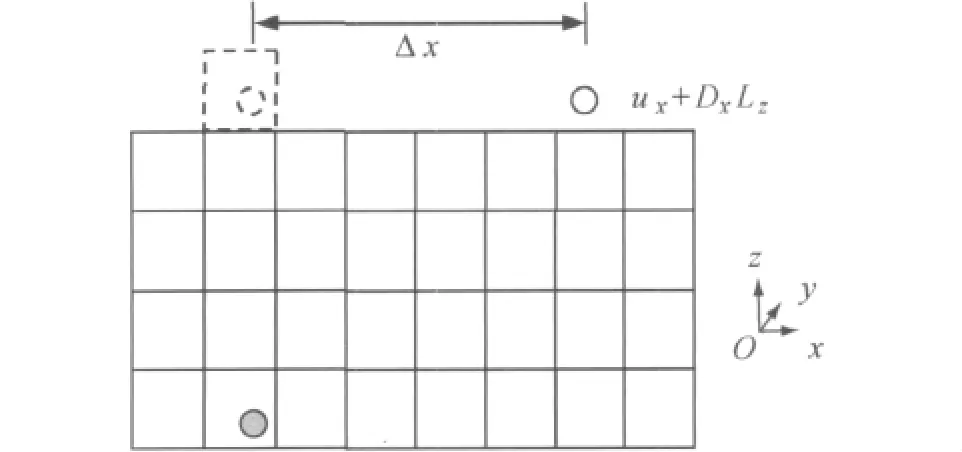
图3 DPD 方法中LE 边界条件的实施Fig.3 Implementation of LE boundary condition in DPD

粒子从计算区域底部离开的算法如下：r′x＝必须强调的是改进的velocity－Verlet算法引入一个中间速度，对于粒子从计算

3 结果及讨论

3.1 LE边界条件下DPD简单剪切流动模拟

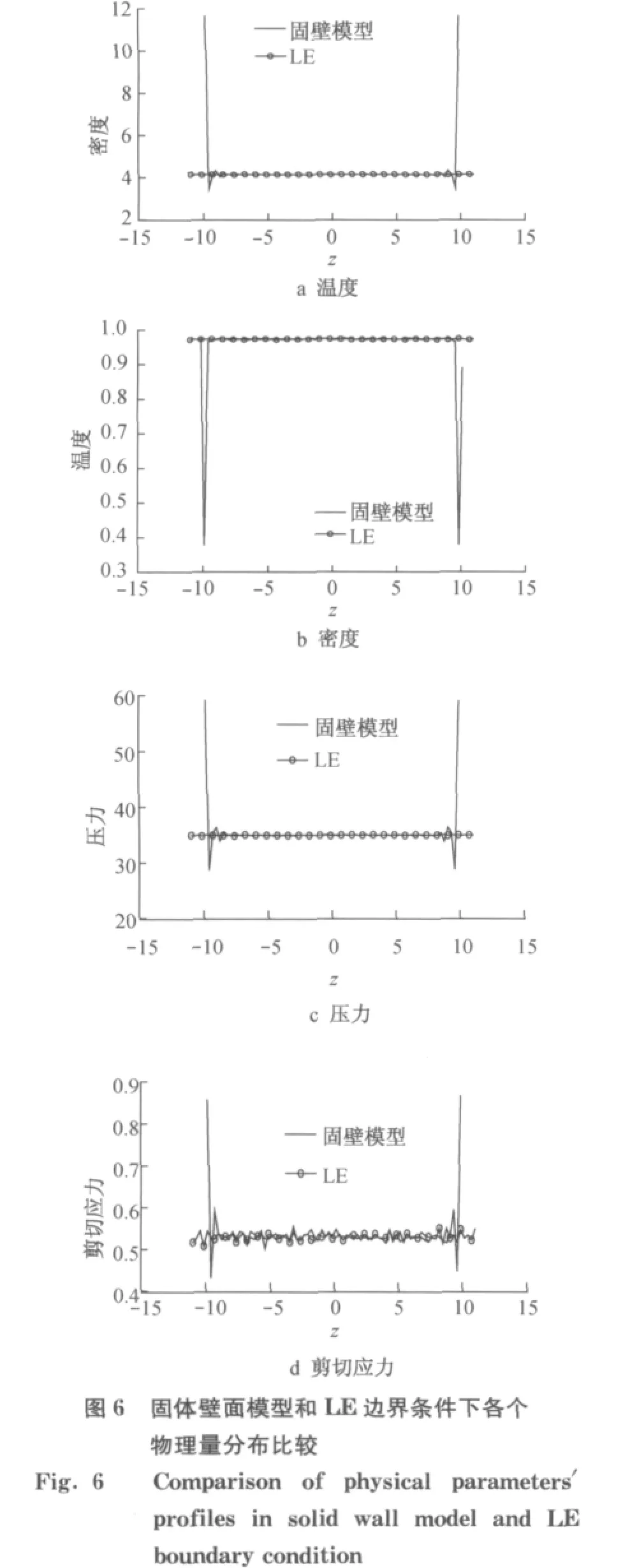
首先，利用上述DPD 与LE相结合的方法，模拟了大小为－15.000≤x＜15.000，－5.000≤y＜5.000，－11.125≤z＜11.125区域内的简单剪切流动.总共采用了27 600个DPD 粒子，由此对应的流体密度为4.13.在开始的2 000时间步长内，令流体粒子自由运动，不施加LE 边界条件，直到达到平衡态.从2 000时间步开始，对系统施加LE 边界条件.时间步长设置为0.02.在z方向设置40 个统计格子，所有的局部参数将由对各个格子内的数据样本进行10 000时间步长的平均而获得.经过45 050步的计算模拟结果如图4所示.

图4 所示为2 种剪切率条件下的简单剪切流动，剪切率分别为0.2和0.4.所得简单剪切流动速度的线性化程度很好，更为重要的是，在边界区域，也即在z＝11.125和z＝－11.125附近区域，模拟的速度没有反常波动，即感受不到边界的存在，说明模拟结果与预想的一致.而其各自的斜率刚好等于剪切率，从而验证了在DPD 中实施LE 边界条件的正确性.相应地，还统计了系统内密度和温度分布.图5所示在剪切率为0.2时的密度和温度分布，显示在边界附近两者均无反常，整个系统的密度保持在4.1附近，而温度也控制在1.0附近.

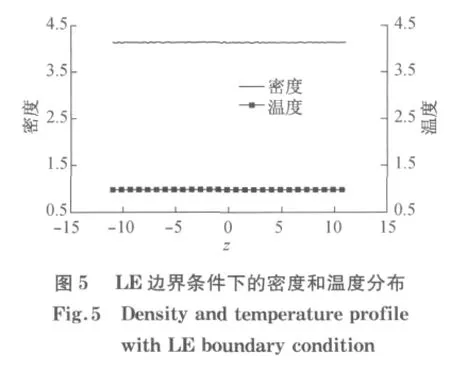
在粒子方法中，如果采用固体壁面模型，在实施无滑移和不可穿透固体壁面条件的同时，很可能会引入壁面效应，对近壁面区域流体参量产生一定的影响.Fan等［17］提出的壁面模型即采用了“冻住”的粒子代表壁面，在壁面附近的流体区域设置一薄层，在这一薄层内流体流动保持无滑移条件，并令薄层内的粒子速度方向随机分布，速度的大小与给定的壁面温度相对应，但各个粒子速度的矢量平均值为零（与静止的壁面相对应）.进一步，令在该薄层内的粒子以一定速度离开壁面，从而保证粒子不穿透壁面.其离开速度式中：vR为随机速度矢量；n为壁面单位法向矢量（指向流体），详见文献［17］.

图6为DPD 方法中采用Fan等［17］提出的壁面模型模拟剪切率为0.2时系统的有关物理量分布与LE边界条件所得结果的对比，图6a显示在壁面附近固体壁面模型产生了一定的密度波动.DPD 中压力和剪切应力的计算可参阅文献［10］.由图6b～6d可见，对LE边界条件来说，本文模拟得到的DPD 系统的温度、压力和剪切应力在边界附近过渡平稳，而采用固体壁面模型所得结果则有较大的波动.

3.2 应用LE边界条件模拟较高施密特数流体的剪切流动

Schmidt数Sc是动量扩散与流体自扩散的比值，本文中采用改进的权函数表达式（式（9）），Sc数可表示为［12］：Sc＝0.5＋（2πγρr4c）2（1999kBT），式中：γ为耗散系数，ρ为密度.传统的DPD 系统所描述的流体Sc数偏低，提高耗散系数是提高流体的Schmidt数的一种有效途径，从而使所模拟的流体更接近实际流体［12］.本文中模拟了σ＝14.14，即γ＝100情况下，时间步长为0.02、计算区域为30.00×10.00×22.25时系统的速度分布.如图7所示，在较高施密特数条件下，剪切率为0.2时，系统内的速度分布仍然是线性的，流动没有边界效应，说明速度梯度在整个空间区域中是均匀的.

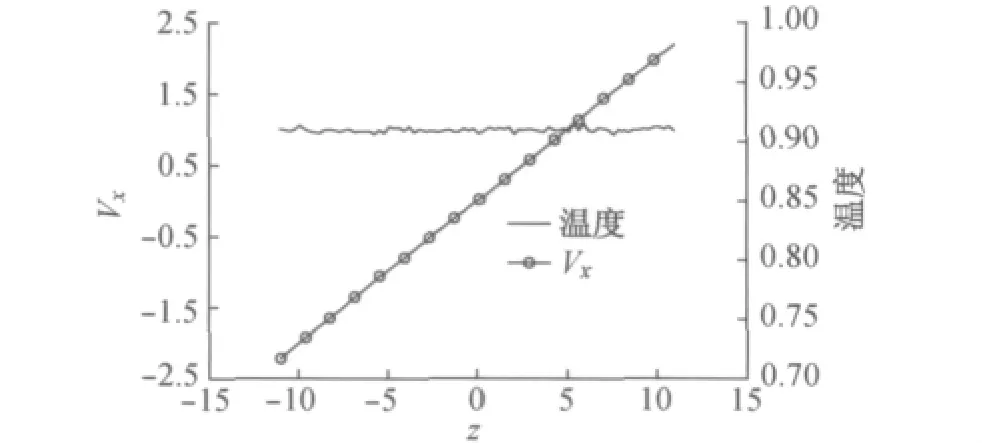
图7 γ＝100时温度及速度分布Fig.7 Temperature and velocity profile whenγ ＝100

文献［21］中显示，当γ＝100时，所模拟的剪切流动在整个系统中不是均匀分布，如图8所示，其线性速度分布出现了转折.文献［21］认为在高的耗散率条件下，LE 边界条件会带来严重的误差，文献［21］将此误差归结为DPD 中耗散力的作用，并需要进行修正才能获得线性的速度分布.不过笔者认为，LE边界条件模拟了一个准无限大区域内的剪切流动，其算法固有的特点是感受不到边界的存在.因此，DPD 中耗散力的影响在整个区域内应当均匀的，而速度分布也应一直保持线性.图7 的结果也支持这个观点.因此本文作者认为，高耗散率条件下，在耗散粒子动力学中应用Lees－Edwards边界条件仍然有效.

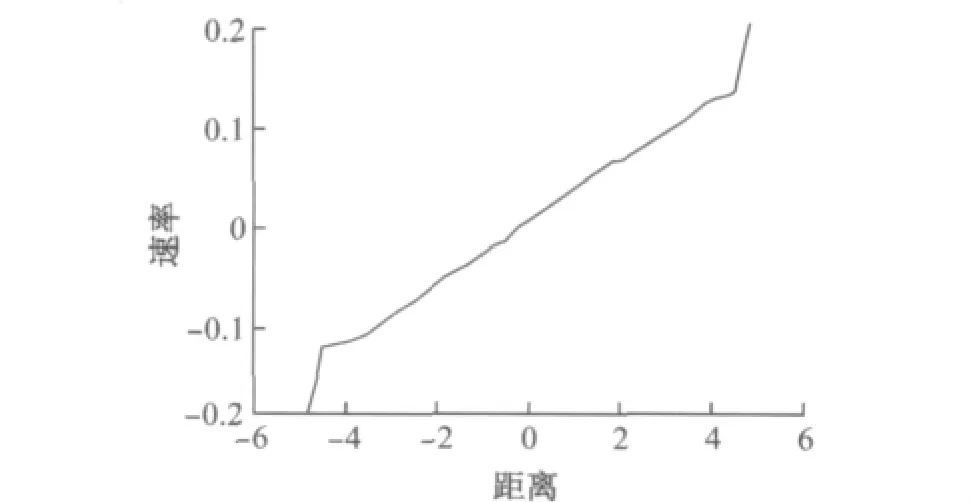
图8 文献［21］中γ＝100时速度分布Fig.8 Velocity profile in Ref.［21］whenγ＝100

Groot和Warren［19］指出随着σ的增加，可能会引起系统温度的不稳定，因此有必要检验σ＝14.14也即γ＝100情况下系统的温度，模拟结果如图7，此时系统温度依然能够很好地控制在0.9～1.0之间.

4 结论

详细讨论了DPD 方法中实施LE边界条件的过程，涉及DPD 方法中改进的velocity－Verlet算法、元胞分割法等与LE 边界条件的结合，并将DPD 方法中现有的一种固体壁面模型与LE 条件所模拟的结果进行了比较.LE条件模拟所得到的速度、密度、温度、压强以及应力分布等均为线性分布，说明流体系统中各参量是均匀的，感受不到计算边界的存在，符合预期.在模拟高耗散率流体的剪切流动时，所得到的速度分布仍然为线性分布，表明LE 边界条件在高耗散率流体的模拟中仍然适用，得出了与文献［21］不同的观点.LE 条件在DPD 方法中的实施可为复杂流体的剪切流动研究提供便利.

［1］ Lees A W，Edwards S F.The computer study of transport processes under extreme conditions［J］.J Phys C：Solid State Phys，1972，5：1921.

［2］ Lorenz E，Hoekstra A G.Lees－Edwards boundary conditions for lattice Boltzmann suspension simulations ［J］.Physical Review E，2009，79：036706.

［3］ Wagner A J，Pagonabarraga I.Lees－ Edwards boundary conditions for Lattice Boltzmann ［J］.Journal of Statistical Physics，2002，107：521.

［4］ 李红霞，强洪夫.耗散粒子动力学模拟方法的发展和应用［J］.力学进展，2009，39（2）：165.LI Hongxia，QIANG Hongfu.Development and application of the simulation method of dissipative particle dynamics ［J］.Advances in Mechanics，2009，39（2）：165.

［5］ 梁文平，杨俊林，陈拥军，等.新世纪的物理化学：学科前沿与展望［M］.北京：科学出版社，2004.LIANG Wenping，YANG Junlin，CHEN Yongjun，et al.The new century physical chemistry：subject front and prospects［M］.Beijing：Science Press，2004.

［6］ Hoogerbrugge P J，Koelman J M V A.Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics［J］.Europhysics Letters，1992，19（3）：155.

［7］ Liu M B，Meakin P，Huang H.Dissipative particle dynamics with attractive and repulsive particle－particle interactions［J］.Physics of Fluids，2006，18：017101.

［8］ Yuan S L，Cai Z T，Xu G Y.Mesoscopic simulation of aggregates in surfactant／oil／water systems ［J］.Chinese Journal of Chemistry，2003，21（2）：112.

［9］ Kong Y，Manke C W，Madden W G，et al.Effect of solvent quality on the conformation and relaxation of polymers via dissipative particle dynamics［J］.Journal of Chemical Physics，1997，107：592.

［10］ Chen S，Phan－Thien N，Fan X J，et al.Dissipative particle dynamics simulation of polymer drops in a periodic shear flow［J］.Journal of Non－Newtonian Fluid Mechanics，2004，118（1）：65.

［11］ Boek E S，Coveney P V，Lekkerkerker H N W.Computer simulation of rheological phenomena in dense colloidal suspensions with dissipative particle dynamics［J］.J Phys：Condens Matter，1996，8：9509.

［12］ Fan X J，Phan－Thien N，Chen S，et al.Simulating flow of DNA suspension using dissipative particle dynamics［J］.Physics of Fluids，2006，18（6）：063102.

［13］ Guo X D，Tan J P K，Zhang L J，et al.Phase behavior study of paclitaxel loaded amphiphilic copolymer in two solvents by dissipative particle dynamics simulations［J］.Chemical Physics Letters，2009，463：336.

［14］ Boek E S，Coveney P V，Lekkerkerker H N W，et al.Simulating the rheology of dense colloidal suspensions using dissipative particle dynamics［J］.Physical Review E，1997，55：3124.

［15］ Español P，Waren P B.Statistical mechanics of dissipative particle dynamics ［J］. Europhysics Letters，1995，30（4）：191.

［16］ Huilgol R R，Phan－Thien N.Fluid mechanics of viscoelasticity：general principles，constitutive modeling，analytical and numerical techniques［M］.Amsterdam：Elsevier，1997.

［17］ Fan X J，Phan－Thien N，Ng T Y，et al.Microchannel flow of a macromolecular suspension［J］.Physics of Fluids，2003，15（1）：11.

［18］ Rapaport D C.The art of molecular dynamics simulation［M］.New York：Cambridge University Press，2004.

［19］ Groot R D，Warren P B.Dissipative particle dynamics：bridging the gap between atomistic and mesoscopic simulation［J］.Journal of Chemical Physics，1997，107（11）：4423.

［20］ Evans D J， Morriss G P. Statistical mechanics of nonequilibrium liquids［M］.Canberra：ANU E Press，1990.

［21］ Chatterjee A. Modification to Lees－ Edwards periodic boundary condition for dissipative particle dynamics simulation with high dissipation rates［J］.Molecular Simulation，2007，33（15）：1233.