基于能耗目标优化的多足爬墙机器人足力控制研究

魏 武 蔡钊雄 邓高燕

华南理工大学，广州，510640

0 引言

多足机器人是仿多足生物运动的一种特种机器人，是一种足式移动机构。常见的多足步行机器人包括四足步行机器人、六足步行机器人、八足步行机器人等。多足爬墙机器人作为一种特殊的多足步行机器人，是应用于高空极限作业的一种自动机械装置，它既具有吸附支持的特殊性，又具有运动形式的特殊性（除了“直立”行走形式外，还有“倒立”、“侧立”和“混立”等行走形式），更重要的是还需要满足高空极限作业的安全性要求。多足爬墙机器人可在核工业、建筑、交通、石化、消防等领域完成检测、探伤、清洗、救援等作业，具有广泛的应用前景。

多足机器人足力控制一直是多足机器人领域的研究重点和难点。近年来国内外学者高度关注多足机器人的足力控制问题，并进行了大量研究。足力控制包括关节驱动力控制和足底接触控制。关节驱动力控制研究方面，具有代表性的研究有Nahon等［1］提出的关节驱动力平方规划方法和Chen等［2］提出的关节驱动力二次优化方法。足底接触力控制研究方面，具有代表性的有：王鹏飞［3］提出的机器人足底接触力虚拟悬挂模型及足底接触力补偿与阻抗控制方法；Spong等［4］提出的被动控制方法；Sangbae等［5］提出的在光滑垂直平面上的足部黏性控制方法；Sang－Ho［6］提出的适应未知外力和粗糙地形的阻抗控制方法；Vidoni等［7］提出的用于解决多种吸附情况下的最小力矩分配问题的静态平衡法。

上述方法只针对关节驱动力或足底接触力进行优化，没有针对能耗目标进行足力的优化，而多足爬墙机器人的能耗问题是高空极限作业需解决的主要问题。本文提出基于能耗性优化的多足爬墙机器人足力控制方法，以八足爬墙机器人为例（四足及六足爬墙机器人类似），在兼顾安全性的前提下，先对机器人的足力优化模型进行讨论，然后再以总电机功率最小为能耗优化目标，对多足机器人的足底接触力进行优化，并给出了电机控制模型的转换方式，最后，对本文提出的优化方法进行实验仿真，证明了所述方法可行有效。

1 基于安全性与能耗目标的足力优化模型

1.1 足力优化模型的转换与简化

本文研究的八足机器人采用真空吸盘式结构，为了分析方便，以八足类爬行动物运动机构为例进行研究［8－9］。机器人由八条腿和躯干共9个相对独立的模块组成。每条腿具有6个自由度，其中髋关节、膝关节、踝关节各有1个自由度，足关节处球铰与真空吸盘相连，组成1个万向关节，具有3个自由度，髋关节、膝关节和踝关节为主动驱动关节，髋关节分别与膝关节和踝关节正交（目前常用的一种方式），髋关节与机体相连接且轴线方向与机体垂直。多足爬墙机器人总体结构如图1所示，关节轴线方向与转动方向以及球铰的运动方向如图1中箭头所示。

1.1.1 关节驱动力和足底接触力的转换

为了实现关节驱动力和足底接触力的转换，本文进行下述处理：

（1）以支撑腿为研究对象，球铰中心为原点（设球铰位于吸盘上），建立特定的坐标系ΣAi（图1），在该坐标系内，第i条腿的连杆平面位于x＊z＊平面内，且z＊轴垂直于吸附平面。

（2）考虑机器人的准静态运动特性（当多足爬墙机器人处于爬行状态时，由于速度较小，所以可以忽略加速度的影响，同时重力主要集中在机体上，可以忽略关节和连杆重力的影响，此时机器人的运动可以看成是准静态运动）。

图1 八足爬墙机器人总体结构图

（3）机器人以一种特定步态沿直线方向爬行，髋关节在爬行过程（包括在水平面及倾斜面爬行的过程）中，转动方向既不需要主动驱动，又不被动承受外扭矩作用，因此由力矩平衡和力平衡条件有τki＝0，si＝0，其中，τki为第i条支撑腿髋关节驱动扭矩，si为第i条支撑腿足底接触力沿y＊轴方向的分力。令机体平面与吸附面保持平行，以腿的连杆平面内的力矩平衡条件可建立以下关系：

为了使各关节电机驱动扭矩均衡化，取τqi＝τhi，则式（1）可化为

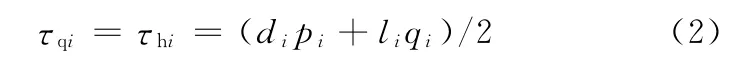
式中，τqi、τhi分别为第i条支撑腿的膝关节和踝关节驱动扭矩；pi、qi分别为第i条支撑腿足底接触力沿x＊、z＊轴方向的分力；di为第i条支撑腿球铰到髋关节轴线的距离；li为第i条支撑腿髋关节与球铰之间的连线在髋关节轴线方向上的投影长度。

通过上述处理完成了关节驱动力向足底接触力的转换。该转换方法实现的前提条件是机器人沿平面做直线爬行，故本文提出的方法只适用于平面环境，但是可以适应于任何角度的斜坡面，包括垂直的斜坡和倒立攀爬的平面。

转换后的模型还减少了优化变量数量：①无需对膝关节轴线和踝关节轴线平行方向的足底接触力进行优化（因为si＝0）；②无需对髋关节的驱动力变量进行优化（τki＝0）；③ 只需对膝关节或踝关节驱动力进行优化（τqi＝τhi）。

1.1.2 关节驱动力约束的转换与简化

关节驱动力约束是由电机的电流和电压受限引起的。每条腿的关节驱动力约束，需要比较膝关节和踝关节最小电流受限驱动力、最大电流受限驱动力、最小电压受限驱动力和最大电压受限驱动力来综合确定。由于关节驱动力约束只需要考虑膝关节或踝关节驱动力约束（τki＝0），所以上述方法中每条腿的驱动约束只有2个关节驱动力约束（前述现有研究方法中，每条腿需要6个关节驱动力约束）。

由于受限驱动力的计算表达式复杂，加上需要比较的次数多，所以确定支撑腿的关节驱动力约束的计算量比较大。为此本文提出一种转换方法来减小确定支撑腿的关节驱动力约束的计算量。即通过比较膝关节与踝关节电机的最大及最小受限力矩，可有效减少确定腿的关节驱动力约束的计算量。具体方法如下：

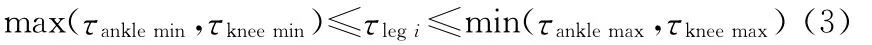
将式（2）代入式（3）可得

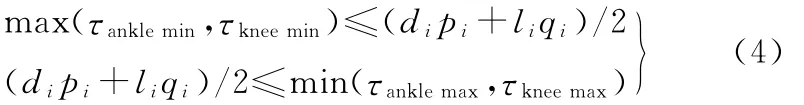
式中，τanklemin、τanklemax、τkneemin、τkneemax分别为踝关节电机和膝关节电机的最小驱动力矩和最大驱动力矩。

式（4）为每条腿的关节驱动力约束，该约束由两个关于pi、qi的线性不等式组成。

1.1.3 动力学约束方程的转换与简化

以机体为研究对象，通过支撑腿建立机体的力和力矩平衡方程，可以建立6个平衡方程（力平衡方程2个和力矩平衡方程4个），转换过程也实现了约束方程的简化，本文中的6个方程只有2n个优化变量（n为支撑腿数量），而前述现有方法中有3n个优化变量。

设机器人所受主矢R＝（Rx，Ry，Rz）和主矩M＝（Mx，My，Mz）的外力作用，各足在机体坐标系Σc中的位置矢量ri＝（rix，riy，riz）（i为腿号），所受接触面作用反力的合力Fi＝（Fix，Fiy，Fiz）。根据力、力矩平衡关系有下列方程：

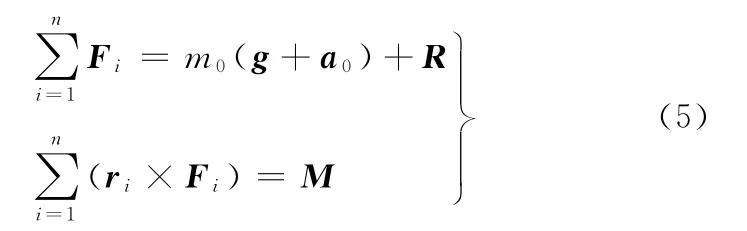
式中，m0为机体的质量；a0为平动加速度；g为重力加速度矢量。

当多足爬墙机器人以静步态直线行走时，可以忽略加速度的影响，因此a0＝0。由zc轴和xc轴方向的力与力矩平衡可以简化得到下面的矩阵方程：

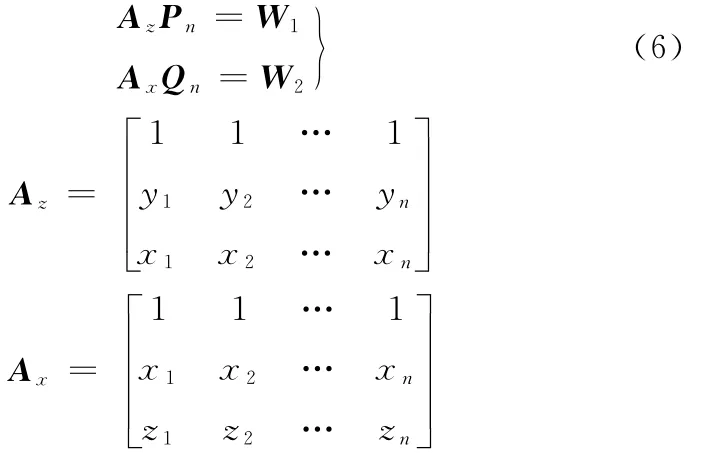
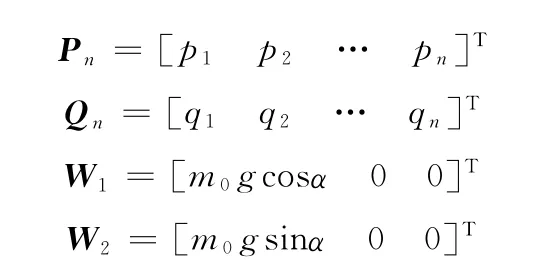
式中，xn、yn、zn分别为各腿髋关节在坐标系Σc中的坐标；α为吸附面法线与重力加速度方向的夹角。

1.1.4 吸盘安全性约束转换与简化

以吸盘为研究对象，建立关于吸盘的力平衡方程［10］。支撑腿足力的反力（实际上是球铰对吸盘的作用力）沿着吸盘吸附面坐标系方向分解合成，得到沿着吸盘吸附面的切向力和法向力，分别为qi和pi，以吸附力方向为正，由吸盘受力关系可以推导出摩擦力约束条件为

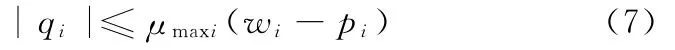
式中，wi为第i条支撑腿真空吸盘压差所产生的对吸盘的垂直压力（简称吸附力，已知）；μmaxi为最大静摩擦因数（已知）。

法向安全约束确保支撑腿吸盘有足够的吸附力，使吸盘不脱离吸附面。由吸盘受力关系可以推导出法向安全约束条件为

本文建立的摩擦力约束为线性不等式约束，优化问题的求解计算量大大减小了。

1.2 基于能耗目标的足力优化

机器人在实际的工作环境中，需要连续长时间运行，其主要的能量均消耗在各个关节的电机之上，其行走方式将成为影响机器人运行能耗的主要因素。为了合理地控制机器人的机械能耗、提高机器人供电电源的续航能力，需要对机器人的能耗目标进行优化。

能耗目标采用使所有关节电机功率总和最小为目标函数，则能耗目标函数可表示如下：

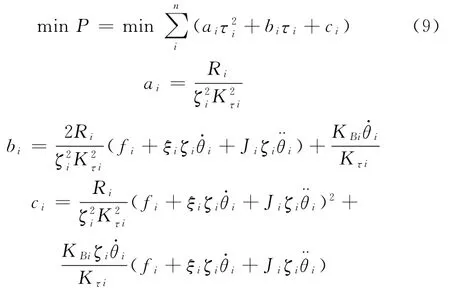
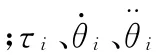
将式（2）代入式（9），以所有支撑腿关节电机功率总和最小为优化目标，优化目标函数可表示为

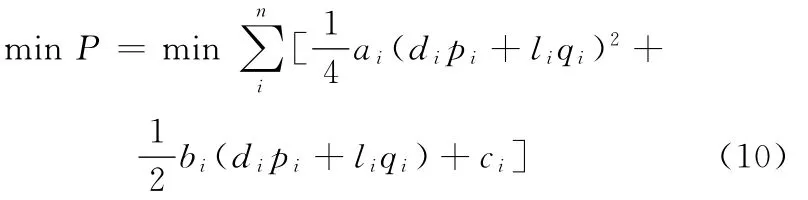
上述优化目标函数具有以下特点：①优化目标函数是关于足底接触力pi、qi的二次函数，保障了优化模型解的连续性；②可以实现足底接触力的优化，结合式（2）可计算出所有关节的驱动力，因此可同步实现关节驱动力优化。

2 足力控制模型与电流控制模型的转换

建立基于足底接触力和驱动力的足力控制模型，实现对足力和足底接触力的同步控制。支撑腿通过髋关节在机体上的作用力可分解成大小和方向与pi、qi相同的两个力，pi、qi作用力的方向分别为髋关节轴线方向和法线方向，可在髋关节上安装传感器测量pi和qi。根据电机电流与关节力矩关系式，建立膝关节驱动力控制模型：

（1）输出测量值。通过pi和qi测量值可以计算出τhi的输出值。

（2）输入参考值。通过优化模型可以求解出pi和qi，代入τhi＝（dipi＋liqi）／2可计算出τhi，作为控制系统的输入参考值。

（3）控制模型。采用电机电流控制模型来实现关节驱动力控制，其模型为

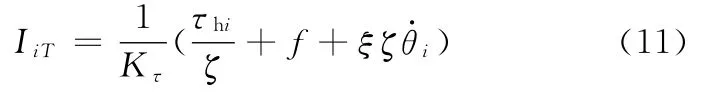
利用式（11）所得电流控制变量IiT，采用三段回路PID控制器就可以获得非常好的电机关节驱动力控制效果。其控制框图如图2所示，实现方法如下：①以IiT为控制变量，电机测量得到的电流、速度和位置作为反馈量，四者的差值作为电流环回路PID控制器的输入量；②以电流环PID控制器的输出量为速度环的输入量；③以速度环PID控制器的输出量为位置环的输入量，位置环的输出量即为满足关节驱动力的实际位置量。

图2 三段回路PID控制规律

3 实验与仿真

为了研究八足爬墙机器人在不同的环境下攀爬所需的最小功率以及所对应的控制规律，使用MATLAB对攀爬不同倾斜平面时机器人的足力控制进行优化。将八足机器人的八条腿分为两组，腿1、2、3、4为一组，腿5、6、7、8为另一组。当其中一组腿的吸盘吸附在攀爬面上时，该组的腿为支撑腿，另一组的吸盘松开，可自由摆动，该组的腿为摆动腿。两组交替摆动运行，完成机器人沿平面直线爬行的步态，如图3所示。图3中，α为吸附平面的倾斜角度，显然，该角即为吸附面法线与重力加速度方向的夹角。

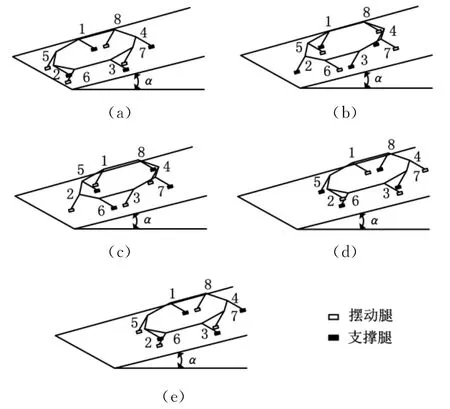
图3 直线爬行步态图

令机器人支撑腿与髋关节轴线的夹角为β，为了既使相邻的两条腿在摆动过程中不出现相互干涉的现象，又使腿有足够的摆动角度，增大支撑腿摆动后机器人本体移动的距离，提高机器人的运动效率，将β的取值范围设定为［－45°，45°］。

在图4所示的吸盘吸附平面中，机器人支撑腿摆动角度为2β＝90°，机器人本体从位置1移动至位置2，设膝关节到球铰的距离（即摆动腿的长度）为S，则有

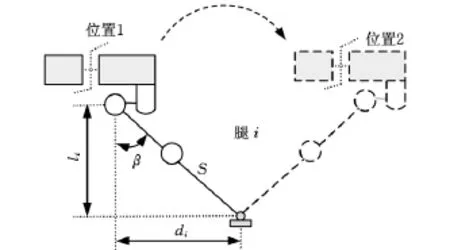
图4 机器人本体前行过程

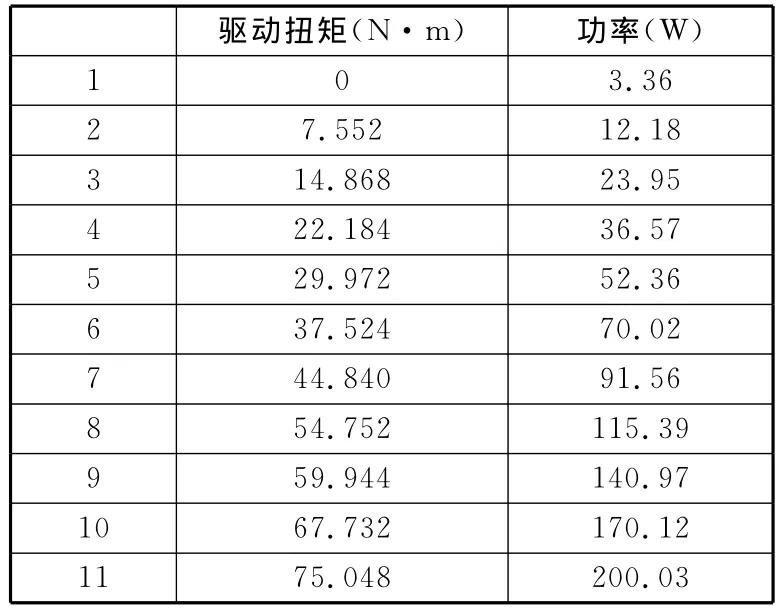
表1 电机功率与扭矩实验数据

对吸盘进行吸附实验，可得最大吸附力wi和最大静摩擦因数μmaxi。膝关节与踝关节采用同一型号电机，则有τanklemin＝τkneemin及τanklemax＝τkneemax。各仿真参数如表2所示。

表2 仿真参数表

根据式（10），取n＝4，以式（4）、式（6）～ 式（8）为约束条件，使用简面体爬山算法（SM）进行优化计算，可得最小总功率min P关于α、β的曲面，如图5所示。

图5 最小总功率min P与α、β的关系

从图5可以看出，由wi＝875N和μmaxi＝0.6所确定的吸盘安全性约束可满足机器人吸附攀爬的需求，其消耗的最小功率与其运动的状况满足直观的规律，具体表现为：当α＝0（机器人正立爬行）及α＝π（机器人倒立爬行）时，机器人支撑腿摆动到β＝0时所需总功率最小，往两边摆动，即｜β｜增大时所需总功率P随之增加；相反，当α＝π／2（机器人在侧立面爬行）时，机器人支撑腿摆动到β＝0时所需总功率最大，往两边摆动，即｜β｜增大时所需总功率P随之减少。

由最优算法计算出当q1＝q2＝q3＝q4、p1＝p2＝p3＝p4时，总功率P最小。以q1和p1为例，α与q1、p1的关系曲线如图6所示。

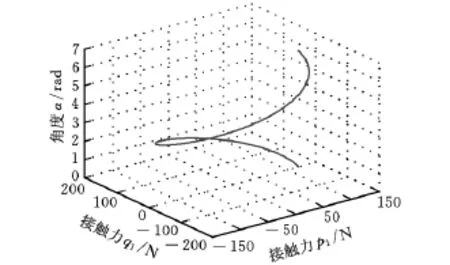
图6 α 与q1、p1的关系

图6说明了多足爬墙机器人在攀爬不同倾斜角度的平面时都有且仅有一组确定的足底接触力qi和pi，使机器人的能耗最小。

根据式（2），将足力控制分量转换为电机的控制扭矩τ1，那么α、β 与τ1的关系曲面如图7所示。

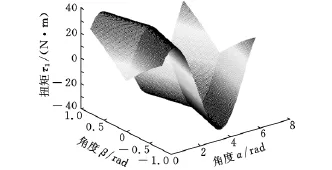
图7 电机控制扭矩τ1与α、β的关系

与图5类似，当α＝0及α＝π时，机器人支撑腿摆动到β＝0时关节驱动力矩τi最小，往两边摆动时，即｜β｜增大时τi随之增大；相反，当α＝π／2时，机器人支撑腿摆动到β＝0时关节驱动力矩τi最大，往两边摆动时，即｜β｜增大时τi随之减少。这是由于式（2）确定了足底接触力与电机扭矩的关系，而足底接触力与最小总功率之间又有唯一确定的关系，故电机控制扭矩与电机最小总功率之间有相似的变化规律。

根据式（11）所述的电机电流控制模型，即可将仿真所得的电机控制扭矩转换为电机的控制电流。

4 结语

本文以八足爬墙机器人为例，描述了多足爬墙机器人的足力优化模型，实现了多足机器人的关节驱动力和足底接触力的转换。建立了多足爬墙机器人总电机功率与机器人的运动步态及作业环境（包括攀爬角度与吸附平面的粗糙度）的关系。在满足爬墙机器人吸附安全性和足力负载均衡的条件下，对机器人的足底接触力进行优化，提高了机器人对环境变化及支撑腿数量变化的适应能力，并降低了关节驱动电机的能耗，实现了机器人电机总能耗最小化的目标。实验仿真结果表明，本文所提出的足力控制方法减少了优化的计算量，实现了关节驱动力和足底接触力的同步控制，优化所得的扭矩控制模型简单直观，便于转换为机器人驱动电机的电流控制模型。

［1］Nahon M A，Angeles J.Optimization of Dynamic Forces in Mechanical Hands［J］.Trans.of the ASME：J.of Mechanical Design，1991，113：167－173.

［2］Chen Xuedong，Watanabe K，Kiguchi K.Force Distribution of a Quadruped Robot［C］／／Proc.of 2000JSME Conf.on Robotics and Mechatronics.Kumamoto，Japan，2000：2P2－43－056.

［3］王鹏飞.四足机器人稳定行走规划及控制技术研究［D］.哈尔滨：哈尔滨工业大学，2007.

［4］Spong M W，Holm J K，Lee Dongjun.Passivitybased Control of Bipedal Locomotion［J］.IEEE Robotics ＆ Automation Magazine，2007，14（30）：30－40.

［5］Sangbae Kim，Spenko M，Trujillo S，et al.Smooth Vertical Surface Climbing with Directional Adhesion［J］.IEEE Transaction on Robotics，2008，24（65）：65－74.

［6］Sang－Ho Hyon.Compliant Terrain Adaptation for Biped Humanoids without Measuring Ground Surface and Contact Forces［J］.IEEE Transaction on Robotics，2009，25（1）：171－178.

［7］Vidoni R，Gasparetto A.Efficient Force Distribution and Leg Posture for a Bio－inspired Spider Robot［J］.Robotics and Autonomous Systems，2011，59（2）：142－150.

［8］Villard C，Gorce P，Fontaine J G.Study of a Distributed Control Architecture for a Quadruped Robot［J］.J.of Intelligent and Robotic Systems，1995，11（3）：269－291.

［9］Liu H Y，Wen Bangchun.Force Distribution for the Legs of a Quadruped Walking Vehicle［J］.J.of Intelligent and Robotic Systems，1997，14（1）：1－8.

［10］Garder J F，Srinivasan K，Waldron K J.A Solution for the Force Distribution Problem in Redundantly Actuated Closed Kinematic Chains［J］.Trans.of the ASME：J.of Dynamic Systems，Measurement，and Control，1990，112：523－526.