高性能同轴式磁力齿轮结构设计与实验研究

杨超君 李志宝 芦玉根 李直腾 杨巧绒 胡 友

江苏大学，镇江，212013

0 引言

工业上广泛采用机械齿轮来达到传递扭矩和改变转速的目的，但是机械齿轮有很多不可避免的缺陷，诸如齿轮之间的机械接触磨损、噪声、振动等，因此越来越多的学者进行磁力齿轮方面的研究［1－4］，磁力齿轮同机械齿轮相比有着很多重要的优点，比如维护少、传动稳定性高、内部可过载保护、输入输出轴之间可物理分离等。磁力齿轮可以在各种不同的嵌入式电动机或发电机中使用，如多电航空引擎、电力轮船推进系统、风力发电机等。随着高性能永磁体的问世，磁力齿轮传递的扭矩密度和效率有了很大的提高［5－6］。

针对高性能磁力齿轮，考虑其结构参数与调磁极片对转矩的影响，本文设计了一种由非导磁材料与软磁材料组合的鼠笼式调磁极片结构［7］。利用Ansoft Maxwell软件对其进行了模拟分析，根据分析结果得出了各种参数的最优值。模拟最优值情况下磁力齿轮的传动性能，并试制了此种参数下的实验样机。通过实验获得了此样机的性能参数，将其与模拟结果进行对比，分析了实验误差产生的原因。最后验证了样机设计的可行性和合理性，同时验证了有限元算法的准确性。

1 高性能同轴式磁力齿轮的结构

如图1所示，最初的磁力齿轮和机械齿轮在结构上差不多，依靠相邻的一系列永磁体直接相互作用来实现扭矩的传递，这种磁力齿轮最大的缺点是扭矩密度很小。尽管此种齿轮的一些改良产品已经相继问世，如文献［8］中提到的采用最适宜的设计参数来增大磁场强度，但由于此种磁力齿轮仍然依靠相邻的永磁体相互作用来产生磁场，而绝大多数的永磁体都没有被利用，所以永磁体利用率较低，扭矩密度远远不能满足工业应用的需求。

图1 最初的磁力齿轮结构

高性能磁力齿轮弥补了上述不足。图2所示为同轴式高性能磁力齿轮的结构模型，此种结构与图1所示结构不同之处在于此种结构中含有调磁极片，通过调磁极片对磁场的调制，所有的永磁体都起到了传递扭矩的作用，永磁体利用率的提升导致扭矩密度大大提高。实际上，这样的磁力齿轮传递的扭矩密度能达到2级和3级螺旋齿轮箱所能传递的扭矩密度［9］。为了减少涡流，提高结构刚度和强度，本文中的调磁极片采用非导磁材料与软磁材料组合的鼠笼式结构，其中非导磁材料为尼龙，软磁材料为硅钢，具有此种结构的磁力齿轮也是本文研究的理论模型。此结构不但能保证调磁极片结构强度和刚度，还能较好地阻止感应电流的轴向流动，从而有效减少涡流，提高效率。

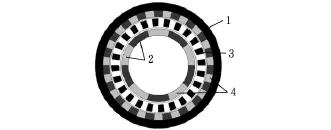
图2 高性能同轴式磁力齿轮的结构

2 Maxwell 2D瞬态分析原理

麦克斯韦方程的运动微分形式可以表示为［10］

式中，Hc为永磁体的矫顽力；v为运动物体的速度；A为磁矢量；Js为电流密度；σ为材料电导率。

在采用Maxwell 2D进行瞬态分析时，固定模型的某一部分使其速度为零，与固定部分有相对运动的物体固定在自身的坐标系内，结合图2，在分析磁力齿轮瞬态气隙磁场时，为模拟磁力齿轮运行时两个转子的相对运动，将调磁极片3的速度设为零，内外转子1、2中的一个速度设为零，同时给内外转子中的另一个加载一个恒定的速度。这时，磁矢量A的偏时间导数变成了全时间导数，因此式（1）变为

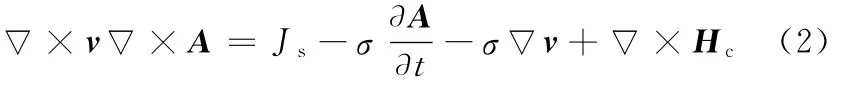
这样，便可以得到有限元模型中每一个时间段内每一个点的参数。由于磁力齿轮的磁场瞬态分布是一个非线性的三维问题，其能量传递的物理过程主要在气隙中发生，而它的气隙尺寸远小于其轴向尺寸，故可忽略端部效应的影响，又因结构的对称性，所以可以把三维磁场问题转化为二维磁场进行分析［11］。可以根据图2建立模型，采用二维有限元软件Maxwell 2D进行模型创建和模拟分析。

3 瞬态磁场模拟分析

3.1 空载磁场模拟

磁力齿轮的结构参数对其性能的影响很大［12］，通过分析可知影响磁力齿轮的主要因素有内外气隙长度、永磁体厚度与长径比。磁能主要储存在气隙中，能量也是通过气隙来传递的；永磁体厚度的变化会引起磁通密度的变化；长径比的大小影响永磁体的利用率。为了确定合理的结构参数，本文设定一种内转子磁极对数Nh为4，外转子磁极对数Nl为19，调磁极片数ns为23的分析模型，在Maxwell 2D中建立模型，然后划分网格，最后施加载荷、进行分析。分析优化值情况下的样例结果如图3所示，通过图3可以直观地了解空载时磁力齿轮的磁场分布和感应电流分布情况。

3.2 结构参数影响分析

3.2.1 传动比的影响

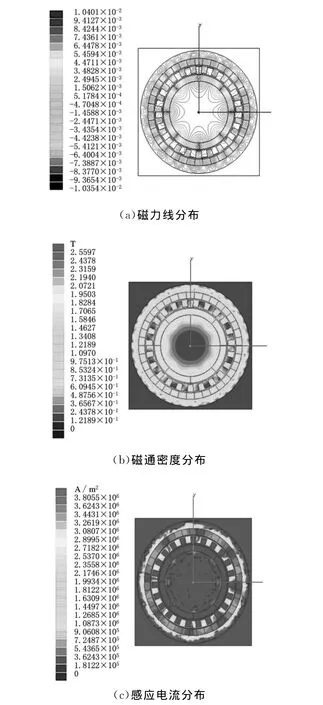
图3 Maxwell 2D分析结果

磁力齿轮的传动比是影响其性能的重要因素之一，设定内磁极对数为4，传动比为3.25、3.75、4.25、4.75、5.25、5.75，模拟得到内外径不变与内外磁极的弧长不变两种情况下输出转矩与传动比的关系图，如图4所示。

图4 传动比与输出转矩关系图

由图4可知，当内外径不变时，磁力齿轮的输出转矩随着传动比的增大而减小，这是由于随着传动比的增大，内磁极对数保持不变，外磁极对数会随之增大，这就造成了磁极之间的漏磁增加，因而输出转矩减小。当保持内外磁极的弧长不变，相应增大磁力齿轮的结构尺寸时，磁力齿轮的输出转矩随着传动比的增大而增大，这是由于随着传动比的增大，外磁极对数的增大会导致永磁体材料的增加，因而输出转矩增大。但通过增加永磁体材料来获得更大转矩的方法是不可取的，因为永磁体材料的价格非常昂贵，所以，当对结构尺寸要求严格时，若想增大输出转矩，应尽量选择较小的传动比。如果适当地增大结构尺寸，可以得到更大的输出扭矩，那么在材料成本上作一定的让步还是可取的，但实际中扭矩的增加量并不是很明显。同时考虑这两方面的影响，实验时传动比设定为4.75。

3.2.2 内外气隙长度的影响

气隙的变化会引起扭矩的变化［13］。为了寻求内外气隙长度与扭矩的关系，分别令内外气隙的 长 度 值 为 1mm、0.9mm、0.8mm、0.7mm、0.6mm、0.5mm，求得内外转子上的扭矩值如图5、图6所示。

图5 内外气隙长度与内转子上传递的扭矩关系图

图6 内外气隙长度与外转子上传递的扭矩关系图

由图5、图6可知，在横坐标方向上，内转矩和外转矩均随着气隙长度的减小而增大。在纵坐标方向上，内转矩和外转矩也是随着气隙长度的减小而增大的，而且增幅较小。这主要是因为随着气隙长度的增大，气隙磁阻增大，消耗在气隙中的磁通势增加，导致输出转矩减小。不过，从模拟数据可以看出，随着气隙的变小，内转矩从2.87N·m增大到3.85N·m，相应的外转矩从13.21N·m增大到17.77N·m。可见，相应的外转矩值是内转矩值的4.6倍左右，这与传动比（4.75）较为符合。因此，在选择气隙长度时，为了提高输出转矩，应根据加工条件尽可能地减小气隙长度。样机制作时内外气隙长度分别选取为2mm、1mm。

3.2.3 永磁体厚度的影响

永磁体厚度的变化会引起磁通密度的变化，从而引起输出转矩的变化。当理论传动比为4.75，模拟永磁体厚度从1mm变化至16mm时，扭矩变化情况如图7所示。由图7可知，随着内外永磁体厚度的增大，输出转矩先增大后减小，这样会有一个相对应的最佳值，即在该点输出转矩达到最大。这主要是因为永磁体厚度变大时，会增大气隙磁通密度，使传递的扭矩增大。但同时，随着永磁体厚度的增大，其所带来的磁阻和漏磁也随之增大，当永磁体厚度增大到一定程度后，所增加的磁势与增加的磁阻和漏磁相当而抵消。如果此时再增加厚度，不仅会浪费材料，而且会使输出转矩减小。根据上述原因，制作样机时永磁体厚度最终选取最优值7mm。

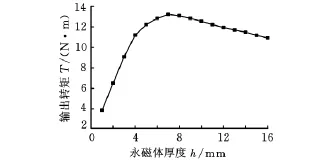
图7 传动比为4.75时永磁体厚度与输出扭矩的关系图

3.2.4 长径比的影响

磁力齿轮的长径比是指其轴向长度与直径的比值，该比值对转矩的影响较大。为了寻求长径比与扭矩的关系，将长径比设置在0.1～1之间，间隔0.1取十个数，分别进行模拟后，得到在不同长径比下的输出转矩如图8所示。从图8可以看出，随着长径比的增大，磁力齿轮输出转矩也随之增大，而上升速率有所下降，长径比与输出转矩成非线性关系。这是由于随着永磁体轴向长度的增大，一方面磁势增大，而另一方面磁阻、漏磁也增大，增加的磁阻、漏磁削弱了增加的磁势。这就使得当永磁体轴向长度增大到一定值后，出现其输出转矩增大速率变慢的情况。为了提高永磁体的利用率，永磁体的轴向长度不宜太大，本实验中取长径比为0.185（25／135）。

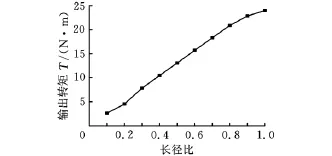
图8 长径比与输出转矩关系图

3.3 优化值模拟

根据上面的分析，磁力齿轮主要参数取值应为：内气隙长度2mm，外气隙长度1mm，永磁体厚度7mm，长径比0.185。依照此优化值模拟得到磁 力 齿 轮 内 转 子 转 速 为 600r／min，750r／min，900r／min、1050r／min、1200r／min、1350r／min、1500r／min、1650r／min时的输出扭矩，其中内转子转速为600r／min、1650r／min时的输出扭矩如图9所示。磁场分布和感应电流分布情况已在图3中示出。

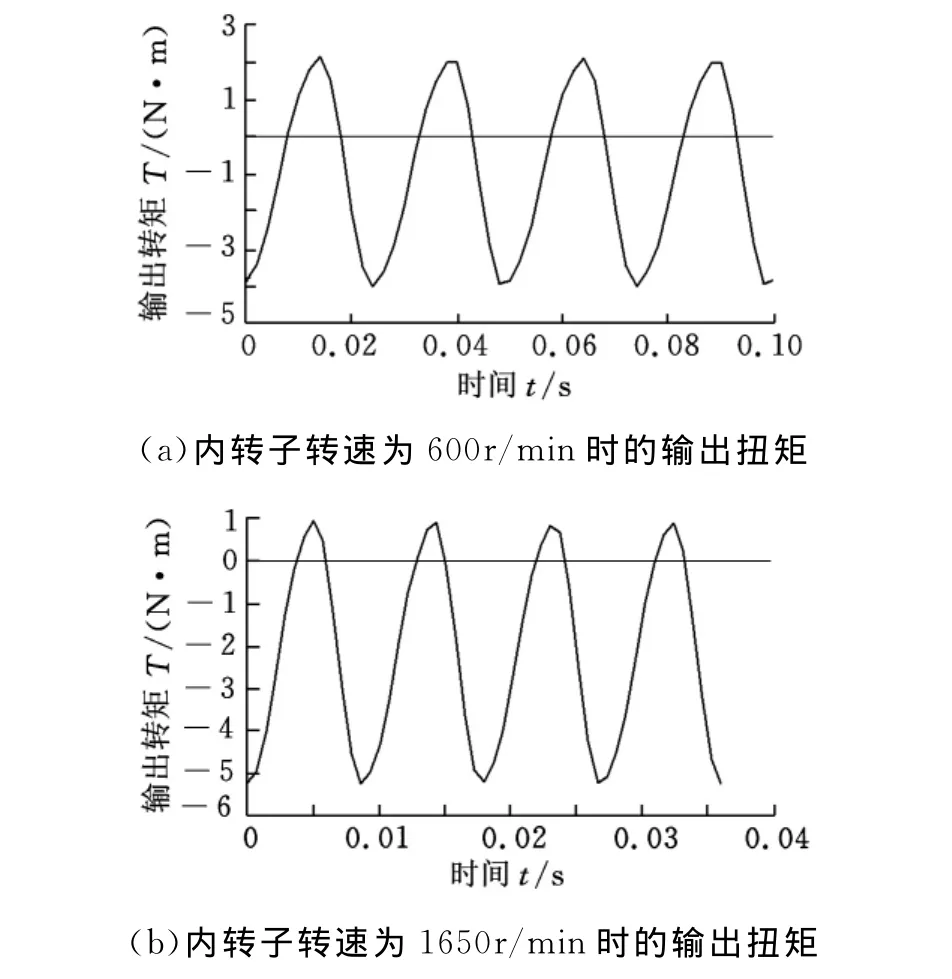
图9 模拟的输出扭矩

4 实验

4.1 实验参数

为了验证采用优化值的磁力齿轮的可行性，试制了样机，样机参数如表1所示。该磁力齿轮模型的有效直径为135mm，有效轴向长度为25mm，内外转子都采用烧结铷铁硼永磁体，其剩磁在20℃时为1.25T，使用厚度为0.5mm、硅含量为3%的硅钢片层叠结构作为调磁极片的材料。考虑加工装配条件，内转子气隙长度选择2mm，外转子气隙长度选择1mm，因为内转矩和外转矩均随着气隙的减小而增大，因此本实验得到的扭矩值可以通过减小内外转子的气隙长度而进一步优化。

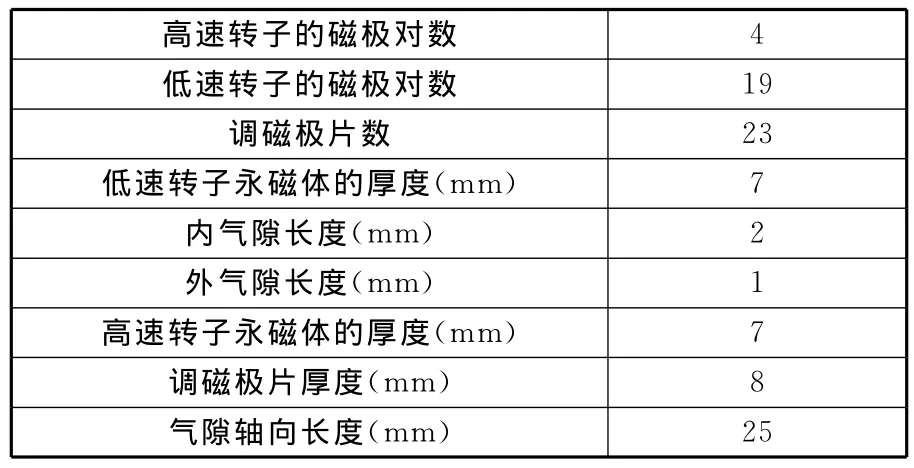
表1 磁力齿轮样机参数

4.2 实验进程

调磁极片对时变磁场的影响很大，为了减少涡流损失，采用层叠结构硅钢片，硅钢片形状如图10a所示。为了使磁力齿轮有较好的机械性能，采用调磁极片固定、内转子驱动外转子的传动形式，因为此种形式对调磁极片的结构强度要求不高。将尼龙棒料做成鼠笼式结构，将硅钢片压入尼龙槽中，图10b所示为安装好的调磁极片，将磁力齿轮安装在图10c所示的实验装置中，以磁力齿轮减速传动为例，即内转子为输入轴，外转子为输出轴进行实验。

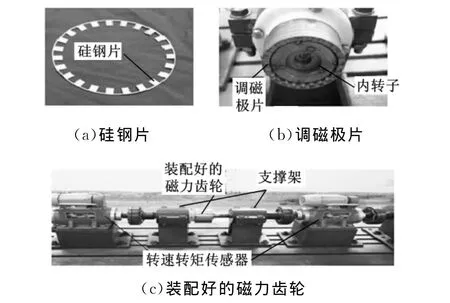
图10 硅钢片、调磁极片以及装配好的磁力齿轮照片

实验时首先尽量地保持输入扭矩不变，调节变频调速器使输入转速逐渐增大，得出输入转速与输出转速的关系，输入功率与输出功率的关系，进而得出效率的变化情况。然后保持转速在较小值不变（598.5r／min），缓慢调节磁粉制动器，使输出扭矩逐渐增大至外转子停转，获得输出扭矩最大值为2.89N·m。

4.3 实验结果分析

由图11可见，磁力齿轮能保持稳定的传动比4.75。实验中传动比曲线有微小波动的主要原因是磁粉制动器控制的输出扭矩有波动，所以导致实验时数据存在微小波动；为了得到输入功率与输出功率的关系，尽量选择输入扭矩稳定在1N·m、输出扭矩稳定在2.3N·m附近的数据，这就导致了输入数据与输出数据截取的时间存在微小差距，进而导致了图中微小的波动。

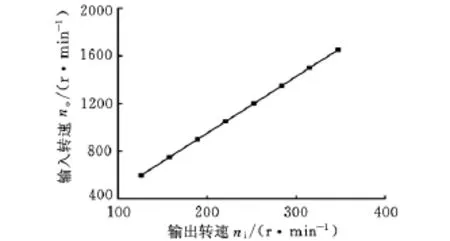
图11 输入转速与输出转速的比值

由图12可见，随着速度的增大，磁力齿轮传动的效率有所减小但是变化不大，在相当大的速度区间内可以基本保持稳定。这主要是因为随着速度的增大，磁力齿轮中磁场变化加快，涡流增大，从而散热量增大，导致了效率的下降。由于本实验选用的磁力齿轮采用鼠笼式结构与硅钢层叠结构相结合的结构，所以既能保证调磁极片的结构强度和刚度，又能很好地阻止感应电流的轴向流动。由于实验过程中，支撑架和联轴器都会有能量损失，所以磁力齿轮实际传递的效率比图12所示的要高。从图12中也可以看出，磁力齿轮在低速运行条件下能够获得较高的效率，而效率整体保持在较低水平，有待于进一步提高。

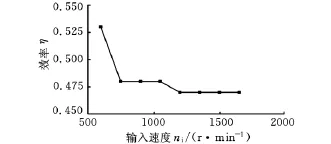
图12 效率随速度变化关系图

由图13可见，当磁力齿轮的输入扭矩保持不变时，随着速度的增大，输入功率与输出功率都会增大。因此，在高速条件下，磁力齿轮的输入功率和输出功率相对较高。这主要是因为，实验时的输入扭矩基本保持在1N·m左右，当转速升高时，根据P＝Tω（P 为功率，T 为扭矩，ω 为转动的角速度）可知，功率会随着转速的增大而增大。

4.4 实验结果与模拟结果对比

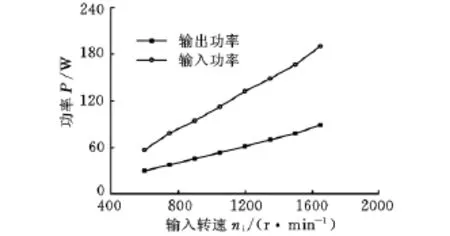
图13 输入输出功率随速度增大的变化情况

通过图10c中转矩转速传感器可以测得各转速下的转矩情况。将实验结果与模拟结果进行对比，如图14所示，从图14可以看出，实验转矩值可以稳定在2.5N·m，而模拟转矩值稳定在3.1N·m，两者相差近0.6N·m，这主要是由以下几方面的原因造成的：模拟时，是将三维模型简化成二维模型来处理的，导致模拟的磁力线只分布在二维平面内，这种处理方式忽略了端部漏磁的影响，而端部漏磁是难以避免的，所以必然会带来一定程度的误差；实验中不可避免地存在机械摩擦损耗，这在模拟时也未予以考虑；加上负载转矩的影响，就会导致实验结果相比模拟结果偏小；另外，二维模拟结果所示为理想状态下的运行情况，末端效应、摩擦、漏磁等都没有考虑，这会导致模拟结果偏大。排除这些因素的影响，模拟结果与实验结果具有相似性，这就说明了设计的样机具有一定的可行性和合理性，同时验证了试制的调磁结构具有调磁效果，能够实现磁力齿轮的定传动比传动。

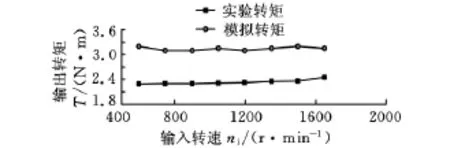
图14 实验转矩与模拟转矩对照

5 结语

本文通过模拟分析得到影响磁力齿轮扭矩传递能力的结构参数优化值，并根据优化值制作了样机，进行了实验验证，实验时样机最大输出扭矩达到2.89N·m。模拟分析与实验结果证明：磁力齿轮输出扭矩与内外转子气隙长度成反比，随内外永磁体厚度的增大先增大后减小，同时随长径比增大呈非线性增大。这些结论验证了磁力齿轮结构设计的合理性与可行性及有限元模型的准确性，这对以后提高同轴式磁力齿轮扭矩承载与结构参数的优化具有重要的指导意义。实验结果相比模拟结果有一定的误差，有待进一步研究，传递能力也有待提高。

［1］张东，邹国棠，江建中，等.新型外转子磁齿轮复合电机的设计与研究［J］.中国电机工程学报，2008，28（30）：67－72.

［2］Fu W N，Ho S L.A Quantitative Comparative Analysis of a Novel Flux－modulated Permanent－magnet Motor for Low－speed Drive［J］.IEEE Transactions on Magnetics，2010，46（1）：127－134.

［3］Frank N W，Toliyat H A.Gearing Ratios of a Magnetic Gear for Marine Applications［C］／／IEEE Electric Ship Technologies.Baltimore，2009：477－481.

［4］William J，Donald M，Timothy F P，et al.Wellbore Motor Having Magnetic Gear Drive： US，7481283B2［P］.2009－01－27.

［5］田杰，邓辉华，赵韩，等.稀土永磁齿轮传动系统动态仿真研究［J］.中国机械工程，2006，17（22）：2315－2318.

［6］Atallah K，Howe D.A Novel High－performance Magnetic Gear［J］.IEEE Transactions on Magnetics，2001，37（4）：2844－2846.

［7］杨超君，李直腾，郑武.一种应用鼠笼式调磁装置的同心磁力齿轮：中国，CN101841280A［P］.2010－09－22.

［8］Kikuchi S，Tsurumoto K.Trial Construction of a New Magnetic Skew Gear Using Permanent Magnet［J］.IEEE Transactions on Magnetics，1994，30（6）：4767－4769.

［9］Atallah K，Calverley S D，Howe D.Design，Analysis and Realization of a High－performance Magnetic Gear［J］.IEEE Proc.Electric Power，2004，151（2）：135－143.

［10］刘国强，赵凌志，蒋继娅.Ansoft工程电磁场有限元分析［M］.北京：电子工业出版社，2005.

［11］Brauer J R，Schaefer S M，Lambert N J，et al.Mixing 2Dwith 3DFinite Elements in Magnetic Models［J］.IEEE Transactions on Magnetics，1990，26（5）：2193－2195.

［12］芦玉根.高性能同轴式磁力齿轮结构参数设计及其实验研究［D］.镇江：江苏大学，2011.

［13］田录林，李言，田琦，等.轴向放置的轴向磁化多环永磁轴承径向磁力研究［J］.中国机械工程，2008，19（10）：1163－1166.