基于质量特性与参数隐式函数关系的DEA混合稳健设计模型

李亚平 刘思峰 方志耕 徐 雷 陶良彦

南京航空航天大学，南京，210016

0 引言

稳健设计作为一种提高产品质量和降低产品成本的有效的工程方法，已经在电子、机械等诸多领域得到推广和应用［1］。稳健设计是使所设计的产品无论在制造还是在使用中当结构参数发生变差，或在规定寿命内结构发生老化和变质（在一定范围内）时都能保持产品性能稳定的一种工程设计方法［2］。稳健设计的目的：①使产品质量特性的均值尽可能达到目标值；②使各种干扰因素引起的功能特性波动的方差尽可能小，这两个目的决定了产品的质量稳健性［1］。相对而言，参数设计阶段更注重产品质量，而容差设计阶段更注重产品的制造成本，容差越小，制造成本越高。因此，现代稳健设计应该在质量和成本的混合视角下进行，即混合稳健设计［2］。

关于混合稳健设计的研究有：陈立周［2－3］提出基于成本－质量模型的混合稳健设计，并给出交互进行优化设计的模型求解方法。耿金花等［4］将与波动相关的质量损失和与容差相关的制造成本综合平衡，基于多响应优化建立了一种多因素、多指标优化的混合稳健设计模型。而关于质量特性和参数隐式函数关系下的稳健设计方法的研究多以响应面法为主，响应面法自Box和 Wilson提出以来，相关的研究非常多［2，4－15］，有一阶响应面模型、二阶响应面模型、双响应面法、多响应面法、混合响应面法、随机响应面法等。不难看出，目前稳健设计模型的研究仍存在以下几方面不足：①文献［2－3］提出的混合稳健设计模型局限于质量特性与参数显式函数关系的情况，并不能解决隐式函数关系问题；②目前解决质量特性与参数隐式函数关系问题的响应面模型存在很大局限性，比如响应值对未考虑到的因素的影响不灵敏以及对拟合的良好性和可检测性要求较高等；③响应面模型并没有考虑容差的制造成本，这不符合稳健设计需要在质量－成本混合视角下研究的实际情况。

针对以上不足，本文提出基于质量特性与参数隐式函数关系的混合稳健设计模型，考虑到探索质量特性和参数显式函数关系的局限性，本模型并不研究质量特性和参数函数关系，而是直接进行稳健设计，利用正交试验工具和数据包络分析（data envelopment analysis，DEA）相对效率评价方法构建一类新的DEA混合稳健设计模型。

1 基于正交试验的参数－容差并行设计

定义1 称y＝（y1，y2，…，ys）为关于产品的质量特性向量，x ＝（x1，x2，…，xm）为关于产品的设计参数向量，Δx ＝ （Δx1，Δx2，…，Δxm）为关于设计参数的容差向量。

由于产品质量问题而导致的损失称为质量损失，质量损失函数是度量质量损失的一种典型方法［2］。 质 量 损 失 函 数 的 通 用 模 型 为：L（y）＝K（y－y0）2，K 是不依赖于y的常数，称为质量损失系数，y为质量特性值，y0是其目标值。y离y0愈近，则L（y）值愈小，表明该项设计的质量损失愈小，功能质量愈好。

定义 2 称 L（y）的期望值 E（L（y））＝K（E（y－y0）2）＝K［σ2y＋（μy－y0）2］为产品关于质量特性的质量损失。

定 义 3 称 E（L（y））＝ （E（L（y1）），E（L（y2）），…，E（L（ys）））为产品关于质量特性的质量损失向量。

定 义 4 称 u（L（y））＝ （1／E（L（y1）），1／E（L（y2）），…，1／E（L（ys）））为产品关于质量特性的用户满意度向量。

由于用户满意度为质量损失的倒数，显然质量特性的质量损失越小，用户满意度越高。

定义5 称c（Δx）＝（c（Δx1），c（Δx2），…，c（Δxm））为产品关于设计参数容差的制造成本向量。

按照正交试验的一般步骤，对参数－容差进行并行试验设计，步骤如下：①选定设计参数，制作参数－容差水平表。选择需要设计的参数，设计参数－容差并行设计的水平表。设各变量的水平数相等，均为p个水平，则参数－容差并行水平表安排见表1。②确定正交试验指标。由于产品关于质量特性的用户满意度体现质量稳健性，产品关于设计参数容差的制造成本体现产品成本，因此将s个用户满意度和m个容差的制造成本作为试验指标。根据设计参数和容差的数目及其水平表，选择合适的正交表安排试验。

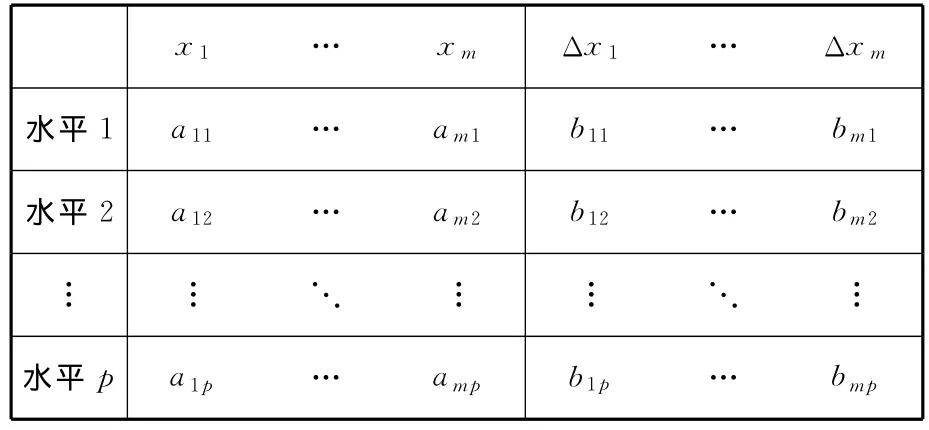
表1 参数－容差并行水平表

根据每组试验得到的质量特性值y及其目标值y0，结合质量损失的定义，得到各组试验方案关于s个质量特性的质量损失向量E（L（y））。

关于制造成本与容差之间的关系已有广泛的研究，常用的模型有指数模型、幂指数模型、多项式模型以及各种复合模型。根据国内中型机械企业的制造水平，中等批量加工时，各类加工特征尺寸的最适用模型［2］已经给出，可根据产品的实际情况选择适当的模型，给出每组试验方案m个容差的制造成本向量c（Δx）。

2 DEA混合稳健设计模型

数据包络分析方法［16］是一种用来评价一组具有多输入和多输出的决策单元（decision making units，DMUs）之间的相对效率的数学规划方法。该方法能够体现最优性价比的思想，将质量和成本融合在一起考虑，最终得到质量－成本相对效率最高的方案。由于交叉效率是利用DEA对决策单元进行充分排序的优化方法，而博弈交叉效率是解决交叉效率解不唯一问题的有效手段［17］，因此，本文采用DEA博弈交叉效率来获得唯一的参数－容差最佳组合。

定义6 设正交试验方案有n组，则称这n组试验方案为n个决策单元，用户满意度和容差的制造成本分别为每个决策单元DMUj的输出指标和输入指标，DMUj的第i种输入和第r种输出分别记作xij（i＝1，2，…，m）和yrj（r＝1，2，…，s）。

基于DEA博弈交叉效率的混合稳健设计模型构建步骤如下。

（1）根据试验结果，建立原始DEA模型。对于任意给定的试验方案DMUd（d ∈ （1，2，…，n）），建立原始DEA模型：

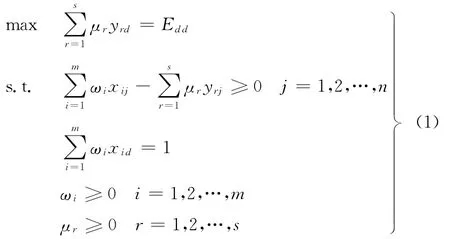
式中，Edd为试验方案DMUd的DEA效率值；wi为第i种输入指标的权重；μr为第r种输入指标的权重。

（2）计算每组试验方案的交叉效率值，实现对n组方案的充分排序。首先计算各试验方案的效率值，得到每组被评价试验方案DMUd的一组最 优 权 重 （ω1＊d，ω2＊d，…，ωm＊d，μ1＊d，μ2＊d，…，μs＊d）。再利用这n组最优权重，求解每组试验DMUj相对于第d组试验DMUd的交叉效率，即

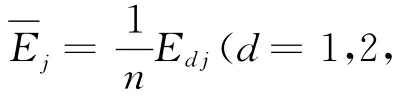
（3）利用DEA博弈交叉效率构建DEA混合稳健设计模型。对于每组试验方案DMUj，在保证第d组试验方案的效率αd不降低的基础上，建立DEA混合稳健设计模型：

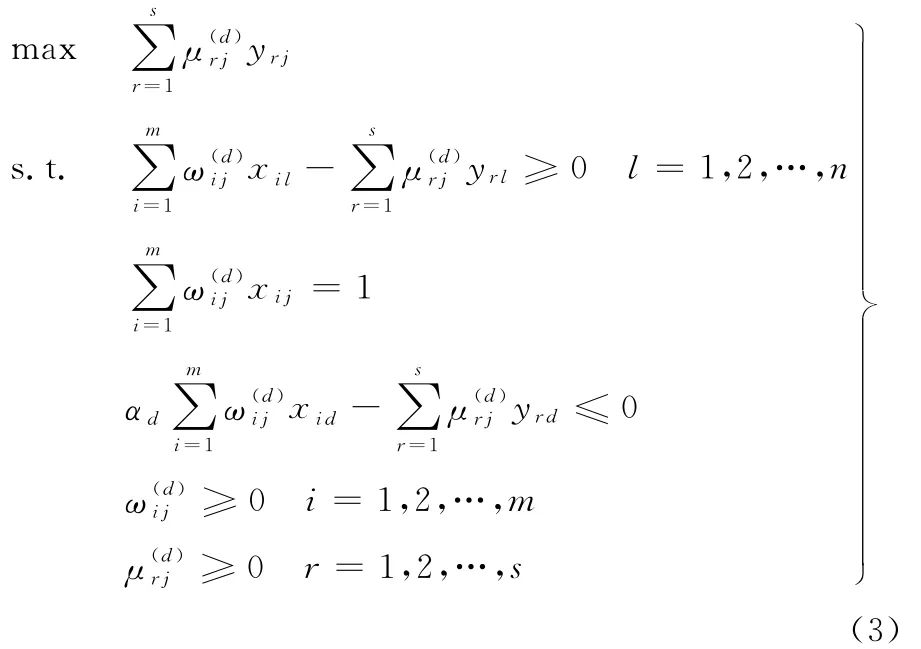
对于每个DMUj，模型将对每个DMUd（d＝1，2，…，n）进行计算，则试验方案DMUj的平均博弈交叉效率为

（4）循环求解式（3），得到每组试验方案的唯一效率值，效率值最大的方案即为最佳参数－容差混合组合。以传统的平均交叉效率值作为αd的初始取值，对于试验方案DMUj，针对每个DMUd，利用初始αd求解式（3），并且将求解到的新的平均目标函数值作为αd，对所有的试验方案重复上述过程，当所有试验方案两次得到的αd差值收敛于ε时，算法终止，最终得出所有试验方案的DEA博弈交叉效率值。每组试验方案的解的唯一性证明参见文献［17］。根据模型的求解结果，将所有试验方案的DEA效率值按大小顺序进行排序，效率值最大的试验方案即为参数－容差混合稳健设计的最佳组合方案。

3 案例研究

图1所示为一个带有电阻R和自感线圈L的电路。电流表A中的电流目标值为y0＝10A；电路两端的电压U＝120V，频率f＝60Hz；电阻R和电感L的取值范围分别为8Ω≤R≤12Ω和0.01H≤L≤0.02H。电阻和电感的容差和价格对应关系见表2。设计该电路，使其达到高质量低成本的目标。

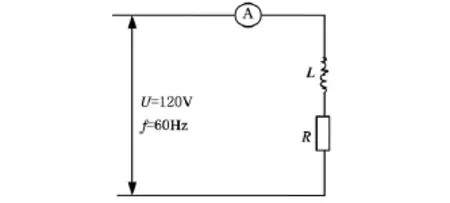
图1 电路示意图

表2 元件容差／价格表

（1）确定可控因素及其水平。根据题意，确定可控因素为电阻R和电感L，对电阻和电感各选定三个水平，即R1＝8Ω，R2＝10Ω，R3＝12Ω，L1＝0.01H，L2＝0.014H，L3＝0.020H。

（2）确定设计变量的容差。不妨对电阻R和电感L这两个设计参数的容差ΔR、ΔL各选定三个水平，即 ΔR1＝0.02Ω，ΔR2＝0.01Ω，ΔR3＝0.005Ω，ΔL1＝ 0.02H，ΔL2＝ 0.01H，ΔL3＝0.005H。

（3）确定正交试验指标。不难看出，题中质量特性仅为电路输出电流，设计参数分别为电阻R和电感L。因此，正交试验的指标为电阻R和电感L 的容差成本c（ΔR）、c（ΔL）（可直接用容差／价格表计算）以及电流稳健性的用户满意度s（y）。显然，电流的质量损失越小，用户满意度越高。

（4）正交试验设计。按照确定的设计参数和容差水平以及正交试验指标，给出质量－成本混合正交试验表，见表3。

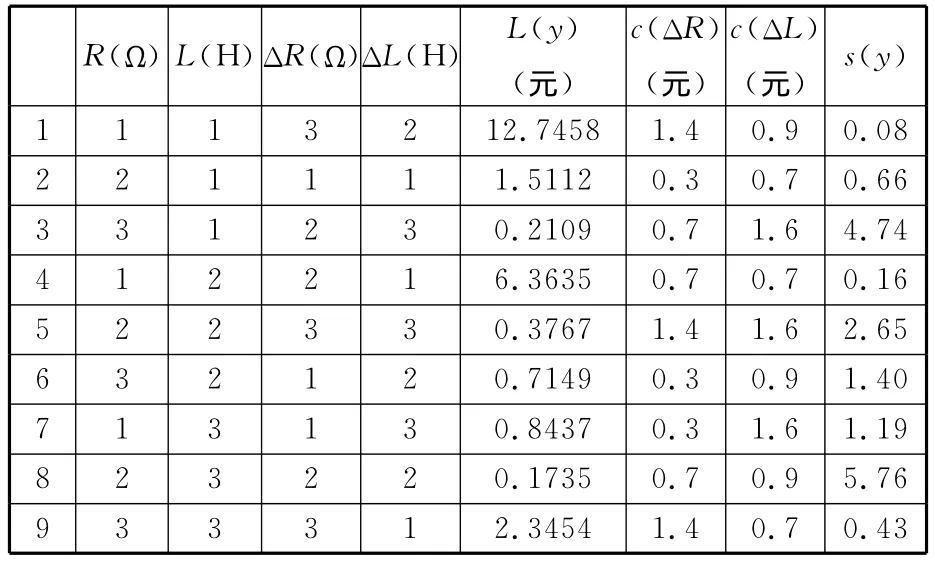
表3 混合正交试验表

（5）DEA混合稳健设计模型求解。从表3中可 以 看 出：c（ΔR）min＝ 0.3，c（ΔL）min＝0.7，s（y）min＝0.08。为便于DEA混合稳健设计模型计算，将c（ΔR）、c（ΔL）和s（y）分别作初值化处理，即作c（ΔR）／c（ΔR）min、c（ΔL）／c（ΔL）min和s（y）／s（y）min处理，结果分别记作c′（ΔR）、c′（ΔL）和s′（y）。c′（ΔR）、c′（ΔL）作为模型输入，s′（y）作为模型输出，取ε＝0.002，模型求解结果见表4。

表4 DEA混合稳健设计模型求解结果

由表4中求解结果的效率排序和用户满意度排序可以看出，两者的排序并不完全一致。用户满意度排序即为质量损失的倒排序，并未考虑成本的影响，这不符合实际情况；而效率排序则考虑制造成本，满足质量－成本相对效率最高的要求才能成为最终的组合方案。第8组试验方案的DEA博弈交叉效率值为1，优于其他组试验方案。因此，满足电路设计的高质量低成本要求的最 佳 参 数 和 容 差 组 合 是：R ＝10Ω，L ＝0.02H，ΔR＝0.01Ω，ΔL＝0.01H。

4 结语

本文提出的模型能够解决质量特性和参数关系未知情形下参数－容差混合稳健设计问题，得到参数－容差设计的最佳组合方案，弥补了以往研究的不足。因此，基于DEA博弈交叉效率的参数－容差混合设计模型在一定程度上完善了目前工程设计方法体系，推动了工程稳健设计的优化进程的发展。

关于质量稳健性的研究非常多，正交试验设计中的质量稳健性指标亦可以尝试用其他指标来衡量；关于容差的制造成本，虽然有经验模型可借鉴，但如何利用更准确的方法去测算成本仍是今后需要进一步探讨的问题；关于成本，如何挖掘得更全面一些亦是今后致力研究的内容。

［1］韩之俊.质量工程学［M］.北京：北京理工大学出版社，1991.

［2］陈立周.稳健设计［M］.北京：机械工业出版社，1999.

［3］陈立周.基于质量－成本模型的稳健优化设计［M］.北京：人民交通出版社，1998.

［4］耿金花，高齐圣，张嗣瀛.多因素、多指标产品系统的建模与优化［J］.系统工程学报，2008，23（4）：449－454.

［5］Lee S B，Park C.Development of Robust Design Optimization Using Incomplete Data［J］.Computers ＆Industrial Engineering，2006，50（3）：345－356.

［6］Köksoya O.A Nonlinear Programming Solution to Robust Multi－response Quality Problem［J］.Applied Mathematics and Computation，2008，196（2）：603－612.

［7］Sun Guangyong，Li Guangyao，Gong Zhihui，et al.Multiobjective Robust Optimization Method for Drawbead Design in Sheet Metal Forming［J］.Materials ＆ Design，2010，31（4）：1917－1929.

［8］Pickle S M，Robinson T J，Birch J B，et al.A Semiparametric Approach to Robust Parameter Design［J］.Journal of Statistical Planning and Inference，2008，138（1）：114－131.

［9］Steenackers G，Guillaume P.Bias－specified Robust Design Optimization：a Generalized Mean Squared Error Approach［J］.Computers ＆Industrial Engineering，2008，54（2）：259－268.

［10］许焕卫，孙伟，张旭.基于混合响应面的多目标稳健设计［J］.机械科学与技术，2008，27（5）：628－632.

［11］杨方，高齐圣，于增顺.多响应问题的稳健性设计优化［J］.工业工程，2010，13（3）：43－46.

［12］何桢，马彦辉，赵有.基于田口过程能力指数和熵权理论的多响应稳健优化设计［J］.中国农机化，2008（3）：33－36.

［13］董恩国，张蕾，孙奇涵.基于双响应面法的行星齿轮机构稳健设计研究［J］.机械传动，2009，33（2）：35－39.

［14］赵媚，潘尔顺，郭瑜，等.基于双响应曲面法的稳健参数设计［J］.工业工程与管理，2010，15（1）：87－91.

［15］乔红威，吕震宙，李洪双.基于随机响应面法的响应灵敏度分析及稳健优化设计［J］.中国机械工程，2009，20（3）：337－341.

［16］魏权龄.数据包络分析［M］.北京：科学出版社，2004.

［17］Liang Liang，Wu Jie，Cook W D，et al.The DEA Game Cross Efficiency Model and Its Nash Equilibrium［J］.Operations Research，2008，56（5）：1278－1288.