大型复杂结构损伤识别两步法研究

李世龙 王天辉 马立元 李永军

军械工程学院，石家庄，050003

0 引言

近几十年来，国内外学者在基于振动的结构损伤识别领域开展了大量卓有成效的研究工作，并已经研究得出很多结构损伤识别方法。常用的方法主要包括基于模态频率和振型的方法［1］、基于柔度曲率的方法［2］、基于应变模态的方法［3］、基于模态应变能的方法［4］、基于结构有限元模型修正的方法［5］，以及基于人工神经网络的智能识别方法［6］等。然而，由于结构损伤识别受到如测量噪声、建模误差、传感器布置数目有限等诸多因素的综合影响，目前尚不存在一种对各种结构都适用且有效的识别方法，各种方法都有其适用范围和局限性，并且大都只适用于一些简单的结构。

目前，对于导弹发射台骨架这种大型复杂结构，仍很少有较为成功的损伤识别方法。本文研究了利用结构的动力测试数据进行发射台骨架损伤识别的方法，通过将基于模型修正的损伤识别方法与模态柔度曲率差方法相结合，提出一种能较好解决这种大型复杂结构损伤识别问题的两步法：第一步，运用基于模型修正的损伤识别方法对损伤进行模糊识别，识别出损伤属于结构的哪个单元组；第二步，运用模态柔度曲率差方法，对损伤进行精确定位。仿真算例及试验验证结果表明，本文提出的损伤识别两步法识别效果较为理想，为解决大型复杂结构的损伤识别问题提供了新思路。

1 基于模型修正的结构损伤识别

笔者基于模型修正技术提出了一种新的结构损伤识别方法，该方法通过建立带边界约束的非线性最小二乘目标函数，将损伤识别问题转化为优化问题，然后采用具有全局快速收敛特性的信赖域方法［7－8］对该优化问题进行求解，从而可以快速准确地识别出结构有限元模型（FEM）各单元组的刚度降低系数，即实现对结构的损伤识别。

1.1 方法的理论基础

结构损伤会导致结构刚度降低，于是结构整体刚度矩阵可以表示为

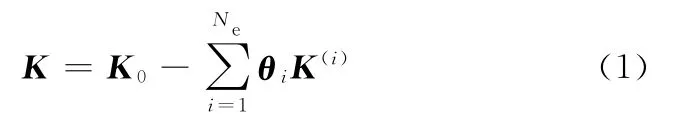
式中，K0、K 为结构损伤前后的整体刚度矩阵；K（i）为结构有限元模型中第i单元的单元扩阶矩阵；θi为Ne维单元刚度降低系数（stiffness reduction coefficients，SRC）向量；Ne为有限元模型中的单元总数。

SRC在本文中代表各单元弹性模量的降低量，用来表征损伤程度的大小。

1.1.1 目标函数的建立

为了极小化有限元模型的计算模态与结构实测模态的差别，目标函数被定义为一个带边界约束的非线性最小二乘的形式：

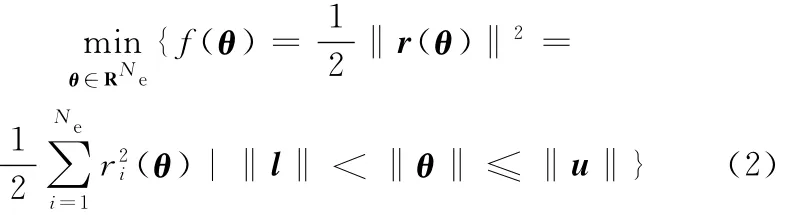
其中，向量l、u∈RNe为待识别参数θ的上下边界。为了满足结构损伤识别的要求，l和u的所有元素都分别被置为0和1。Nm维目标函数向量r（θ）由频率和振型两部分信息组成，表示如下：

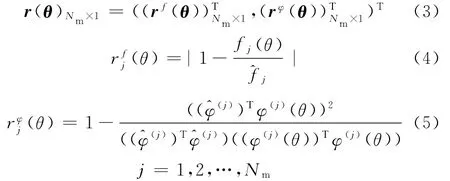
其中，fj（θ）、φ（j）（θ）分别表示第j阶自振频率及振型，上标“＾”表示该参数实测模态数据，Nm维向量rf（θ）用来衡量各阶自振频率的相近程度，Nm维向量rφ（θ）用来衡量各阶振型的相近程度，它包含各阶振型的模态置信度（modal assurance criterion，MAC）。模态置信度用于描述振型的相关程度。

当采用式（2）所示的最小二乘形式时，目标函数的梯度向量和Hessian矩阵都具有其特殊的简化形式，即均可用一阶偏导形式的Jocabian矩阵来表示，克服了每次迭代中需计算二次导数矩阵（Hessian矩阵）的困难，很大程度上提高了计算效率。

1.1.2 目标函数的求解

由于信赖域方法既具有牛顿法的快速局部收敛性，又具有理想的全局收敛性，因而本文采用信赖域算法求解上述带边界约束的非线性最小二乘问题，从而识别结构各单元组刚度降低系数。收敛准则定义为：｜（f（θk）－f（θk－1））／f（θk－1）｜＜ε，即目标函数的前后两次迭代值误差小于某一给定精度。本文收敛精度ε取为1.0×10－6。

1.2 数值仿真及试验研究

1.2.1 发射台骨架的模态试验

试验时，将发射台骨架离散为25个节点，每个节点按3个自由度考虑，以便获取发射台骨架的三维模态。根据发射台骨架模型的几何特点，选取其中的15个节点作为测量点，共测量28个自由度方向。各测点的自由度分布见表1。

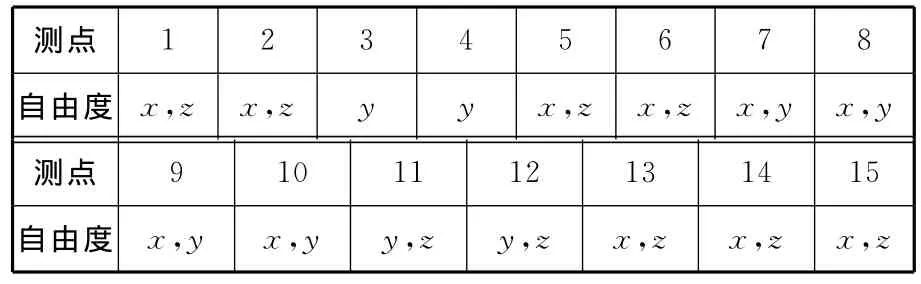
表1 发射台骨架各测点自由度分布

用橡胶绳将模型悬吊起来，使其处于“自由状态”（无边界约束状态）。采用锤击法进行激振，单点激励，多点响应。采样频率为10kHz，每个响应信号取2048个采样点。加速度信号经电荷放大器放大进入DH5920动态信号测试分析系统，测试分析软件采用东华模态分析软件（DHMA）。本发射台骨架模型的测点编号分布及试验现场如图1所示。

图1 发射台骨架模型的测点编号分布及试验现场

1.2.2 发射台骨架的有限元建模及修正

为了获得与实际结构的动力特性比较接近的有限元模型，本文建立了发射台骨架的三维实体有限元模型，如图2所示。但是在这种情况下，整个数值模型太过于复杂和庞大，单元、节点及自由度数目相当可观，采用信赖域算法对其进行反复迭代计算及修正时，计算量相当大。因此在模型修正及损伤识别的第一步中，本文对该模型进行了单元分组，将各个单元组作为一个整体来进行模型修正及损伤识别。

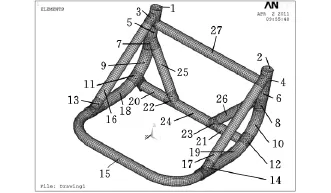
图2 发射台骨架有限元模型及单元组划分

由于本文建立的有限元模型的几何尺寸（截面特性及各部件长度等）及材料特性等均是按设计要求完成的，所以这些因素在模型修正过程中可以不予考虑。本模型为钢管焊接结构，具有多个焊缝，焊接过程中焊缝及其周围材料的特性变化较大，这将成为有限元模型误差的主要来源。

运用上文提出的模型修正方法，对发射台骨架焊接节点上各单元组（3，4，7，8，11，12，13，14，22，23）的材料特性进行修正，修正后有限元模型的计算模态和实测模态的比较见表2。从表2可以看出，修正后的有限元模型的计算模态和实测模态很接近，说明该有限元模型可用于后续的损伤识别。

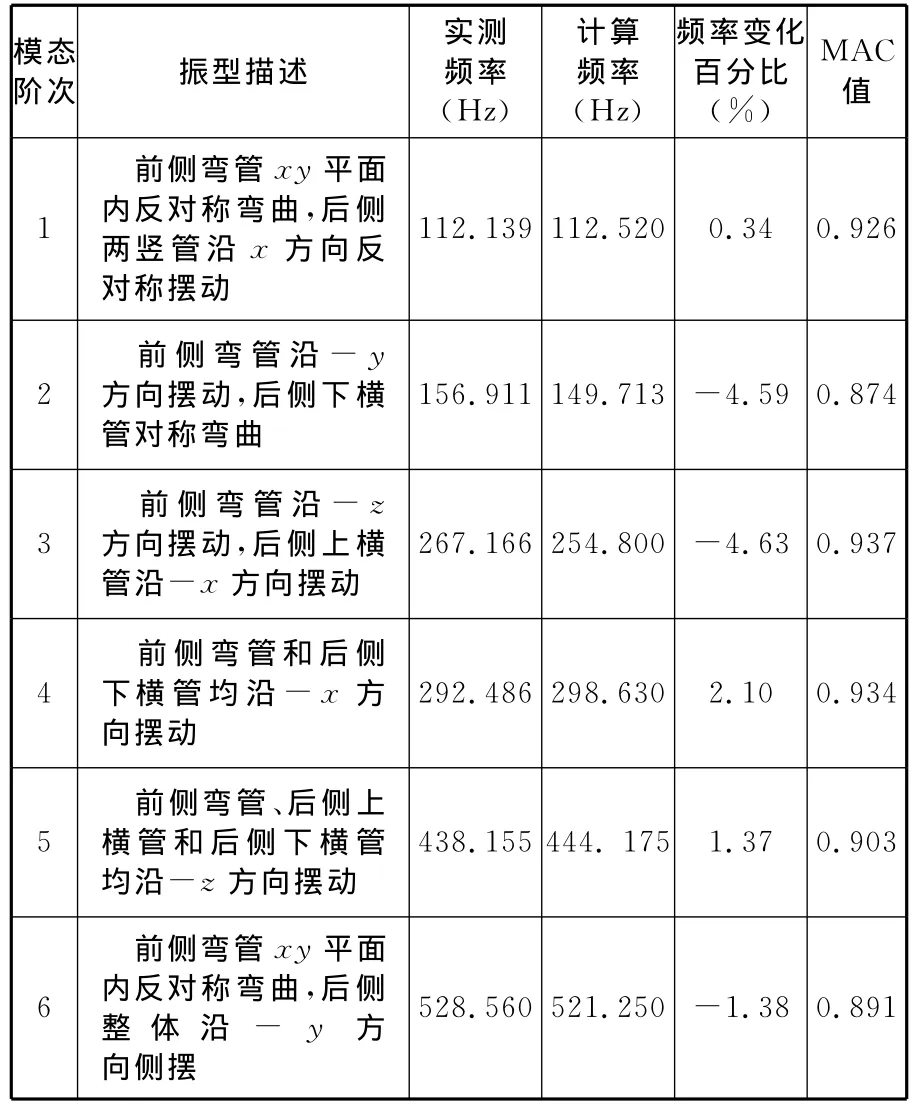
表2 修正后有限元模型的计算模态和实测模态的比较

1.2.3 损伤识别数值仿真研究

（1）损伤工况设置。本文对发射台骨架单损伤（工况1）、两损伤（工况2）和微小损伤（工况3）3种工况进行数值仿真研究。其中，工况1假定24号单元组发生30%的损伤（刚度降低30%）；工况2假定在单元组24和27处均发生30%的损伤；工况3假定24号单元组仅发生10%的损伤。表3表示3种工况下发射台骨架模型损伤前后的频率变化。从该表中可以看出，工况3的各阶频率变化都不明显。从这里就可以看出，在这种微小损伤引起的频率改变不明显的情况下，仅利用频率进行损伤识别是不够的，还需要将频率与振型一起利用起来进行损伤识别。本文所提出的方法正是同时利用了频率与振型信息。

表3 发射台骨架有限元模型损伤前后的模态频率及其变化

（2）损伤识别结果分析。通过定义刚度降低系数来反映各单元组损伤的程度。从3种损伤工况的识别结果（图3）可以看出，本文所提出的方法对于发射台骨架这样的大型复杂结构的损伤识别是可行的。特别对于工况3下的微小损伤，本方法也取得了较好的识别效果，说明本文提出的损伤识别方法具有较高的灵敏度。

1.2.4 损伤识别试验数据验证

（1）损伤工况设置。对发射台骨架试验模型仍设置了3种损伤工况，分别如下：①24号单元组从左至右1／4处被切开，深度为钢管外半径的一半（a＝12mm），如图4所示；②24号和27号单元组从左至右1／4处均被切开，深度均为钢管外半径的一半；③24号单元组从左至右1／4处被切开，深度仅为钢管的壁厚（a＝5mm）。发射台骨架试验模型损伤前后实测频率和振型的比较分别见表4和表5。

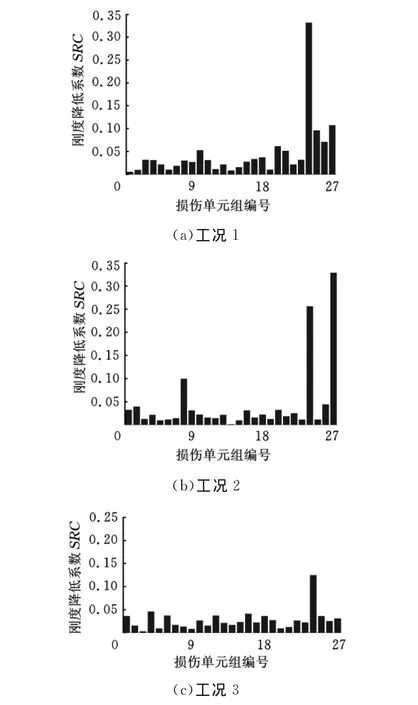
图3 损伤识别结果

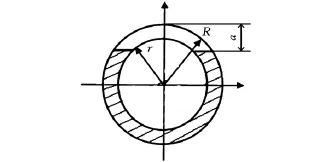
图4 钢管损伤后截面示意图

表4 发射台骨架损伤前后实测频率（Hz）比较

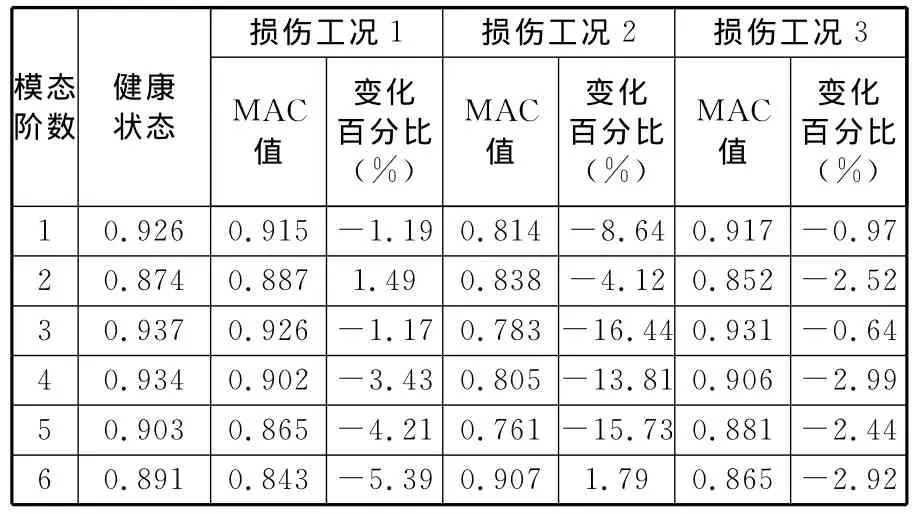
表5 发射台骨架损伤前后实测振型与修正后有限元模型之间的MAC值比较

（2）损伤识别结果分析。从三种工况的损伤识别结果（图5）可以看出，实际发生损伤的单元组基本可以识别出来。特别对于工况3下的微小损伤，由于本方法充分利用了损伤前后的振型和频率信息，也实现了损伤的识别，说明本文提出的损伤识别方法具有较高的灵敏度。但由于发射台骨架结构本身的复杂性及模态试验中存在的误差等原因，识别结果还不够清晰。

图5 损伤识别结果

2 基于模态柔度曲率差的结构损伤识别

上文运用基于模型的损伤识别方法对发射台骨架进行了损伤的模糊识别，得出了损伤属于哪个单元组，但具体位置还不够精确，下面运用基于模态柔度曲率差的损伤识别方法对损伤进行精确定位。

Pandey等［9］的研究表明：利用柔度矩阵的改变量对结构进行损伤识别，比固有频率或振型对局部损伤进行识别更敏感。本文在前人的基础上，提出了一种识别结构局部损伤的新方法——模态柔度曲率差方法。

2.1 方法介绍

本方法在求模态柔度曲率差之前，先求损伤前后模态柔度的曲率矩阵Fu和Fd，其元素计算如下：

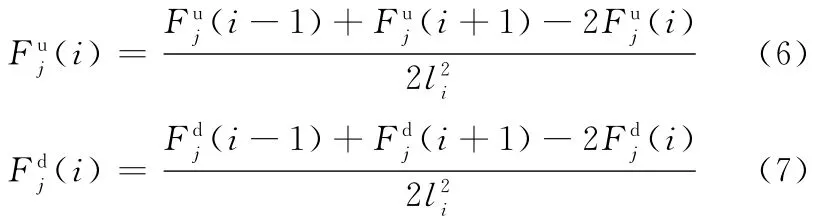
式中，Fuj（i）、Fdj（i）分别为损伤前、损伤后柔度矩阵第j列第i行的元素；li为第i单元的长度。

模态柔度的曲率矩阵差值为

将曲率差矩阵ΔF中每行按节点进行叠加取平均值，再按节点将均值组成新的列矩阵：

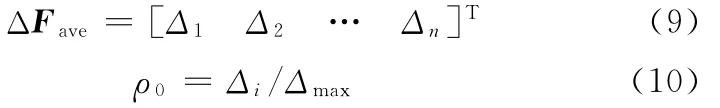
式 中，i 为 节 点 或 测 点，i ＝ 1，2，…，n；Δmax为 Δi的最大值。

ρ0与节点位置一一对应，其大小反映了结构损伤后柔度曲率变化的急剧程度，称为模态柔度曲率差。当结构局部出现损伤时，结构的局部刚度降低、局部柔度增大，损伤位置的柔度曲率亦增大。如果相邻两节点处的模态柔度曲率差远大于其余节点的模态柔度曲率差，则这两点之间的单元就是损伤单元。

2.2 试验及结果分析

将单元组27划分为15个小组，从左至右共布置16个传感器（图6），测量其损伤前后的局部模态，提取结构的前几阶固有频率和局部振型。测量总共进行两次，测量自由度首先为x方向，待测量完毕后将传感器调整为z方向。根据式（6）～式（10），编制 MATLAB程序，绘制模态柔度曲率差ρ0随节点变化的二维曲线，并将两次测量结果所得曲线进行拟合，则曲线突变处将指示出损伤的精确位置（图7）。

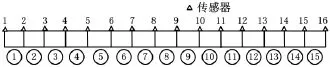
图6 单元组27的分组及传感器布置

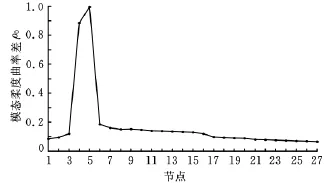
图7 模态柔度曲率差损伤识别结果

工况2中27号单元组的实际损伤位置设置在从左至右四分之一处，即位于节点4和节点5之间。从模态柔度曲率差的识别结果可以看出，节点4和5处曲线突变很明显，因此运用模态柔度曲率差方法可以实现损伤的精确定位。

3 结语

本文提出了一种基于模型修正和模态柔度曲率差的大型复杂结构损伤识别两步法。该方法将损伤识别分为两步：第一步，运用基于模型修正的损伤识别方法对结构损伤进行模糊识别，识别出损伤属于结构的哪个单元组；第二步，运用模态柔度曲率差方法，对损伤进行精确定位。对某导弹发射台骨架的数值仿真及试验研究结果表明，本文提出的损伤识别两步法识别效果较为理想，为解决大型复杂结构的损伤识别问题提供了新的思路。

［1］Shi Z Y，Law S S，Zhang L M.Damage Localization by Directly Using Incomplete Mode Shapes［J］.Journal of Engineering Mechanics－ASCE，2000，126（6）：656－660.

［2］瞿伟廉，陈超.基于应变模态的钢结构构件焊缝损伤定位方法的研究［J］.世界地震工程，2002，18（2）：2－7.

［3］曹晖，张新亮，李英民.利用模态柔度曲率差识别框架的损伤［J］.振动与冲击，2007，26（6）：116－120.

［4］Law S S，Shi Z Y，Zhang L M.Structural Damage Detection from Incomplete and Noisy Modal Test Data［J］.Journal of Engineering Mechanics－ASCE，1998，124（11）：1280－1288.

［5］徐伟华，刘济科.基于移动载荷响应的多跨连续桥梁损伤检测［J］.力学与实践，2008，30（5）：49－52.

［6］张德海，朱浮声.结构损伤智能诊断研究进展［J］.力学与实践，2003，25（4）：1－5.

［7］Conn A R，Gould N I M，Toint P L.Trust－region Methods（MPS／SIAM Series on Optimization）［M］.Philadelphia：Society for Industrial Mathematics，1987.

［8］Branch M A，Coleman T F，Li Y.A Subspace Interior and Conjugate Gradient Method for Large－scale Bound－constrained Minimization Problems［J］.SIAM Journal on Scientific Computing，1999，21（1）：1－23.

［9］Pandey A K，Biswas M.Damage Detection in Structures Using Changes in Flexibility［J］.Journal of Sound and Vibration，1994，169（1）：3－17.