超弹性蒙皮蜂窝芯的设计及等效模量研究
2012-12-03彭海峰董二宝张世武
彭海峰 董二宝 张世武 杨 杰
1.中国科学技术大学,合肥,230027
2.中国科学院长春光学精密机械与物理研究所,长春,130033
0 引言
智能变形飞行器能够通过改变自身外形来实现更高的气动效率,已经成为航空航天飞行器发展的一个重要发展方向。传统蒙皮起着维持飞行器外形,直接承受气动载荷并将其传递到飞行器内部横纵向受力构件上,同时在机翼发生变形时承受相应的弯矩和剪切力的作用[1]。变形飞行器的发展,对飞行器机翼蒙皮又提出了一些新的要求,即需要拥有特定方向和较低的面内模量来节省变形能的同时,在其他方向又具有较高的承载能力,避免表面因气动载荷而发生过大的变形[2-5]。
目前,对可变形机翼蒙皮的研究主要集中在以下两个方向:一种是滑动蒙皮,该结构利用蒙皮壁板间的相对错位滑动实现变形,承载刚度和强度较高,变形范围也比较大,但是变形柔韧性差,质量较大且表面光滑程度不足,影响整体机翼的气动性能;另一种是柔性蒙皮,该结构利用柔性材料或功能材料的大应变实现变形,柔韧性好,但是承载刚度和强度较差[6-7]。设计一种质量小、柔韧性好、承载能力高,同时保证表面光滑变形的蒙皮,成为变形飞行器研究领域的热点和难点之一。
蜂窝结构以其质量小、强度和刚度都较高等诸多优点,在航空航天领域得到了广泛应用[6-10]。将传统蜂窝结构表层面板替换为硅胶或超弹性聚合物等柔性材料,形成蒙皮基体,并对蜂窝芯结构的形状和结构进行优化设计,有望实现综合性能优良的柔性可变形蒙皮。
笔者所在的课题组以传统的六角形蒙皮单元为优化对象,以气动承载能力强和实现蒙皮单轴方向柔性大变形为优化目的,将传统的六角形蒙皮单元优化成为一种性能优良的蛇形环蒙皮单元。在机翼弯曲变形时发生延展的方向,蒙皮的共面刚度较小,在垂直于蒙皮的方向,由于蜂窝自身强度和表面覆盖的弹性材料的强度都较高,因此可以承受较大的气动载荷。
本文采用了理论建模、有限元仿真和力学参数测定试验三种方式对这种超弹性蒙皮单元的共面变形刚度进行分析,得出了蛇形环蒙皮单元在弹性变形情况下x、y方向的等效弹性模量的工程计算方法,为蜂窝夹层结构的工程应用提供设计参考。
1 蛇形环单元介绍
蛇形环单元的示意图见图1,这种蒙皮单元类似于弯曲的蛇由焊点连接在一起,故将其命名为蛇形环,每个单元由4个长度为l、厚度为t的直肋壁和6段半径为r、厚度为t的弧肋壁组成。
利用蛇形环蜂窝结构作夹层内芯,将硅胶等柔性材料或形状聚合物等功能材料覆盖在蜂窝结构表面来保持表面变形的柔顺性。该结构在需要变形的方向有较低的面内模量,在其他方向有较高的承载刚度。
此种单元可以应用到自适应机翼的蒙皮中(图2),以变弯度翼的后缘向下弯曲为例,机翼后缘的上表面蒙皮单元的沿翼弦方向发生拉伸,下表面蒙皮的翼弦方向发生压缩。因此,可变形蒙皮在机翼弦向方向的弹性模量应尽量小。

图2 蛇形环单元在自适应机翼中的位置
2 蛇形环蜂窝弹性模量
设蜂窝基材的密度为ρs,一般t≪l,t≪r,则蜂窝芯的密度为

假设蒙皮单元各部分发生线弹性小变形,则横向(即x方向)应力σ1(图1)引起x方向加载时,受力及力矩情况如图3a所示。
根据平衡条件,图3a中A、D两点的力矩和简化集中力分别为

式中,b为蛇形环z方向的厚度;rm为中面半径。
由能量法可知,蜂窝芯夹层结构在x方向上的等效弹性模量为
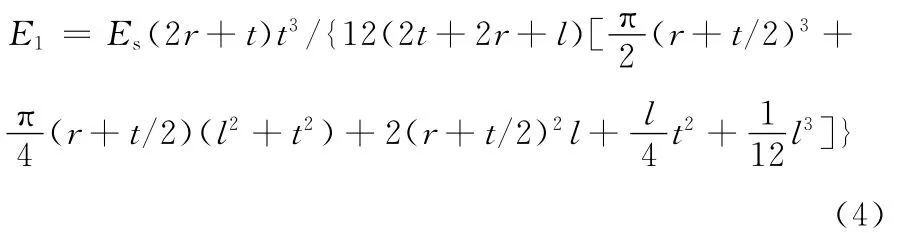
式中,Es为材料的弹性模量。
同理,对于y方向加载的情形(图3b),由平衡条件可知:

式中,M1、W 分别为E、H两点的力矩、简化集中力;σ2为纵向(即y方向)应力(图1)。
同理可得蜂窝芯夹层结构在y轴方向上的等效弹性模量为
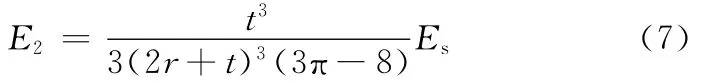
3 单元的数值模拟计算
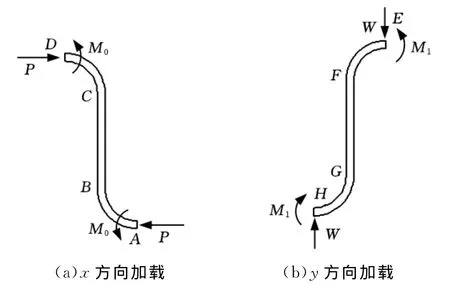
图3 蛇形环单元共面单轴受力及力矩情况
为求得蛇形环蜂窝夹芯的等效弹性参数,鉴于仿真对象为单个单元,本文采用精度较高并适合超弹性模型的Solid186单元进行分析。在对x方向等效弹性模量的分析中,对单元左侧的平面施加全向的自由度约束,对另一侧的平面施加压力载荷,根据试验测试选用的材料,设置材料弹性模量Es=3GPa,通过有限元数值模拟求出应变。图4为蛇形环单元的仿真变形图。
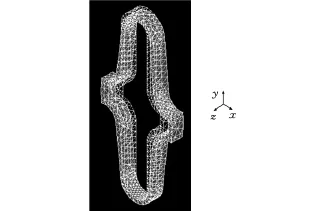
图4 蛇形环单元仿真变形图
4 几何参数对单元参数的影响
蜂窝芯结构的等效弹性模量除了与构成蜂窝胞元的材料常数有关,还与蜂窝芯的几何形状与尺寸有关。
为了验证有限元分析和理论分析的正确性,采用有机玻璃加工单个蜂窝单元的样品,并对其进行力学性质测定试验,得到相应的力学参数测定结果。
图5所示为分别由有限元分析、试验和理论计算得到的l、t、r三个几何参数对蛇形环横向的等效弹性模量的影响。
图5a给出了t=1.2mm、r=5mm时E1随l的变化规律,可以看出,E1随l的增大而减小;图5b给出了l=20mm、r=5mm时E1随t的变化规律,可以看出,E1随t的增大而增大;图5c给出了l=20mm、t=1.2mm时E1随r的变化规律,可以看出,E1随r的变化不是很明显。
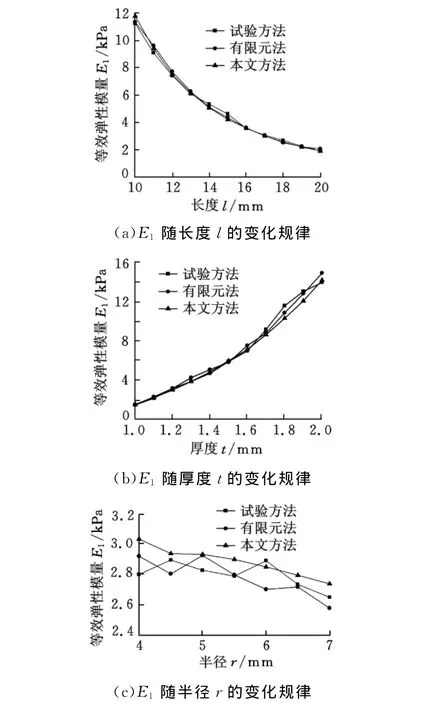
图5 不同结构尺寸和E1关系
表1所示为不同材料尺寸下y方向等效弹性模量的试验值和仿真值的比较。由图5和表1可知:蛇形环单元的y轴方向的等效弹性模量明显大于x方向的等效弹性模量;y方向的等效弹性模量随壁厚度t和直板部分长度l的变化较明显。
上述分析表明,三条曲线吻合程度良好,证明了等效弹性模量公式和有限元仿真的准确性。

表1 不同材料尺寸下y方向等效弹性模量E2实验值与仿真值对比
5 结束语
本文在线弹性小变形假设条件下利用能量法理论推导出了一种蛇形环蜂窝芯结构的共面等效弹性模量求解公式。通过理论计算、有限元仿真和试验测试的数据对比表明,给出的等效弹性模量公式具有较高的精度。最后探讨了结构参数对蜂窝芯共面等效弹性弹性模量的影响,为基于蛇形环蜂窝芯的柔性可变形结构设计与优化提供了参考。
[1]王志瑾,姚卫星.飞机结构设计[M].北京:国防工业出版社,2007.
[2]Jha A K,Kudva J N.Morphing Aircraft Concepts,Classifications,and Challenges[C]//Smart Structures and Materials 2004Conference.San Diego,CA,2004:213-224.
[3]Mehta V,Frecker M,Lesieutre G.Contact-aided Compliant Mechanisms for Morphing Aircraft Skin[C]//Conference on Modeling,Signal Processing,and Control for Smart Structures.San Diego,CA,2008:9260-9264.
[4]dos Santos e Lucato,Wang J,Maxwell P,et al.Design and Demonstration of a High Authority Shape Morphing Structure[J].International Journal of Solids and Structures 2004,41(13):3521-3543.
[5]杨志春,解江.自适应机翼技术的分类和实现途径[J].飞行力学,2008,26(5):1-4.
[6]Xu X F,Qiao P Z,Davalos J F.Transverse Shear Stiffness of Composite Honeycomb Core with General Configuration[J].Journal of Engineering Mechanics-ASCE,2001,127(11):1144-1151.
[7]Thill C,Etches J,Bond I,et al.Morphing Skins[J].Aeronaut Journal,2008,112:117-139.
[8]Scarpa F,Tomlin P J.On the Transverse Shear Modulus of Negative Poisson’s Ratio Honeycomb[J].Fatigue & Fracture of Engineering Materials& Structurals,2001,23(8):717-720.
[9]McKnight G P,Henry C P.Large Strain Variable Stiffness Composites for Shear Deformations with Applications to Morphing Aircraft Skins[C]//Conference on Behaviorand Mechanics of Multifunctional and Composite Materials.San Diego,CA,2008:92919-92919.
[10]梁森,陈华玲.圆柱形胞元蜂窝夹芯板梁理论的研究[J].复合材料学报,2005,22(2):137-142.
