基于禁忌搜索的平行机多工厂供应链调度

蒋大奎 李 波

天津大学，天津，300072

0 引言

对于一些大型装备制造项目，装备制造企业需要多个零部件加工厂为总装工厂提供装配部件。企业普遍采用的项目实施流程为：企业总部将工件分配给多个零部件加工厂，并要求在指定期限内完成工件生产并送至总装工厂，各个零部件加工厂需要在指定期限内以最低的生产和运输成本完成总部分配的任务。由于总部与零部件加工厂存在着不同的资源约束和决策目标，当各部门独立决策时，难以实现企业整体利益最大化。如何通过对工件分配、工件生产和运输调度协同优化以降低企业内部供应链成本，成为这类企业关注的热点问题。

为了有效地解决这类问题，供应链调度问题（supply chain scheduling）被提出，并受到广泛关注。供应链调度问题将排序理论应用于供应链管理，对生产调度和分批发送2个阶段的问题集成研究，从具体操作层面使用确定性模型研究供应链问题［1］。文献［2－4］分别研究了单机器和平行机单工厂供应链调度问题，但并没有考虑订单运输时间和车辆装载能力约束。针对上述研究的不足，文献［5－8］提出了启发式算法以求解考虑订单运输时间和车辆装载能力约束的单机器和平行机单工厂供应链调度问题。对供应链中有多个工厂的情况，由于需要考虑订单分配，问题的复杂性明显增加。Chen等［9］研究了单机器作业环境下的多工厂供应链调度问题，证明了问题是NP难题，并设计了启发式算法。蒋大奎等［10］将文献［9］中的客户数量扩展为多个，并设计了混合禁忌搜索算法进行求解。在多工厂供应链调度问题中，目前尚没有关于工厂为平行机作业环境的相关研究报道［11］。

针对零部件加工厂普遍为平行机作业的特点，本文提出一类平行机多工厂供应链调度问题，为该问题设计了一种基于向量组编码结构的禁忌搜索算法，并通过仿真实验验证了平行机多工厂供应链调度的优越性和本文禁忌算法的有效性。

1 问题描述及最优性条件

1.1 问题描述

本文的问题描述如下：某企业在不同地理位置共有m个零部件加工厂，零部件加工厂集合记作M＝｛1，2，…，m｝。每个零部件加工厂i的加工环境为具有ri台相同的机器，在任意时刻，每台机器只能加工一个工件。计划期内企业需要加工n个工件（订单），工件集合记作N＝｛1，2，…，n｝，每个工件仅需在一台机器上加工一次。工件j在工厂i的加工时间为pij，加工成本为cij。工件加工后按批次发送给总装工厂，每个批次最多发送b个工件。工厂i发送一个批次的运输时间为ti，运输成本为fi。所有工件必须在交货期限D内送至总装工厂。企业需要将工件分配给各个零部件加工厂、安排工件在各台机器上的加工顺序以及对如何分批发送工件进行决策，通过制定集成调度方案（以下简称方案）以使完成所有工件的生产和运输总成本最小。为方便，将本文问题简记为P。问题P的结构如图1所示。

图1 平行机多工厂供应链调度问题结构图

为方便表达，本文采用三参数法（δ，σ，φ）描述一个方案，其中参数δ表示一个订单分配子方案，它指定了每个工件的加工工厂；参数σ表示δ给定下的一个生产调度子方案，它指定了加工每个工件的机器及加工顺序；参数φ表示σ给定下的一个分批运输子方案，它指定了工厂的发送批次数、每批次的发送时间及工件所在的发送批次。

1.2 最优性条件

定理1 对于问题P，存在具有以下性质的最优调度：

（1）同一个工厂加工任何2个工件之间没有空闲。

（2）每一批工件的发送均发生在该批工件中的某一个工件的加工完成时间。

（3）每个工厂加工的所有工件按加工完成顺序进行发送。

记集合Ni（σ）为生产调度子方案σ指定的由工厂i加工的工件集合，Ni（σ）中工件数量为ni（σ）。

定理2 当δ和σ给定时，问题P具有一个最优的分批运输子方案φ＊。将每个集合Ni（σ）中的所有工件分成yi个批次发送，yi的计算公式为

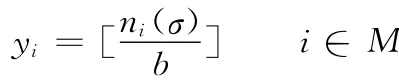
其中，第一个批次发送ni（σ）－（yi－1）b个工件，其余的yi－1个批次均发送b个工件。

定理1的结论显然成立，定理2的证明见文献［11］的定理7。

通过上述定理，问题得到简化。简化后问题的决策变量为xijk＝1，即工件j由工厂i的第k台机器加工，否则为0；yi为工厂i发送的批次数。

借鉴文献［9］单机器多工厂供应链调度问题的数学模型，问题P的混合整数规划模型可以表示为

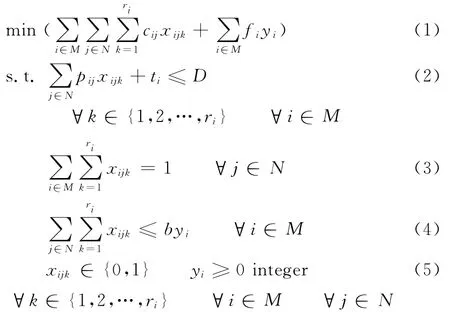
其中，目标函数式（1）的第一项表示完成所有工件的生产总成本，第二项为运输总成本；约束式（2）表示各机器加工的工件必须在交货期限内完成；约束式（3）表示每个工件的加工需求均要得到满足，且只能由一台机器加工；约束式（4）为发送批次的约束。

2 禁忌搜索算法设计

禁忌搜索算法（taboo search algorithm，TS）作为一种求解全局优化问题的智能优化算法，广泛应用于NP－hard组合优化问题的近似求解［12－13］。针对问题特点，本文设计了一种基于向量组编码结构的禁忌搜索算法及3种邻域操作。

2.1 编码结构

图2 6个工件的2个双机器工厂的向量组

2.2 初始解

初始解的生成步骤如图3所示。

图3 生成初始解的流程图

2.3 邻域操作

若当前解为不可行解，本文设计了块结构邻域操作以搜索可行解；若当前解为可行解，本文设计了插入、交换2种邻域操作以搜索邻域中更优的解。

2.3.1 块结构操作

块结构操作由Nowicki等［14］首先提出，并广泛应用于生产调度问题。本文设计了一种块结构邻域操作以处理当前解为不可行解的情况，块结构邻域操作的具体步骤如下：

（1）记当前解中违反交货期限约束的机器在向量组中对应的向量为Vak，从Vak中任选一个元素A。

（2）在向量组中任选一个向量Vbl，Vak≠Vbl，在向量Vbl中任选一个元素B。将元素A从Vak中取出，并插入到元素B前面或将元素A与元素B交换。

（3）记向量Vak中由工件组成的集合为Na，向量Vbl中由工件组成的集合为Nb，分别判断以下2个公式是否成立：

若均成立，则执行步骤（4）；否则，块结构操作得到的解为不可行解，块结构操作终止。

（4）由向量组得到订单分配子方案δ′和生产调度子方案σ′，由定理2得到分批运输子方案φ′，新的方案（δ′，σ′，φ′）生成，块结构操作完成。

2.3.2 插入操作和交换操作

插入操作通过将向量组中某个向量的元素插入到其他向量中，以得到新的订单分配子方案δ′和生产调度子方案σ′，再由定理2得到新的分批运输子方案φ′。

交换操作通过交换2个不同向量中的元素，以得到新的订单分配子方案δ′和生产调度子方案σ′，再由定理2得到新的分批运输子方案φ′。

借助德国卡尔蔡司偏光显微镜观察C/C试样的金相结构.在MM-W1型立式万能摩擦磨损试验机上进行摩擦磨损试验(见图1).C/C试样的对磨销为40Gr钢,硬度HRC45,规格为Φ5.5 mm×10 mm,表面粗糙度Ra0.8µm.

2.4 禁忌规则和终止条件

本文算法的禁忌规则为：如果向量Vik中的工件j移动到其他向量中，则在接下来的λ代中不允许工件j被移回到向量Vik。如果经过邻域操作得到比当前解更好的解，则不管该邻域操作是否被禁忌，都采用该邻域作为当前邻域。终止条件为达到预先设定的迭代次数μ。

2.5 算法框架

禁忌搜索算法框架如图4所示。

3 独立决策策略

本文设计了独立决策下总部的订单分配问题模型和各零部件加工厂的生产运输集成调度问题模型。

3.1 订单分配问题模型

为了缩短项目周期，总部以完成所有工件的时间最小化为决策目标。对于该订单分配问题，本文作以下假设：

（1）工厂为机器作业环境，工厂i加工工件j的加工时间为pij／ri。

图4 禁忌搜索算法框架

（2）每个加工完成的工件单独运送。

订单分配问题的决策变量为zij＝1，即工件j由工厂i加工，否则zij为0。其订单分配问题的数学模型为

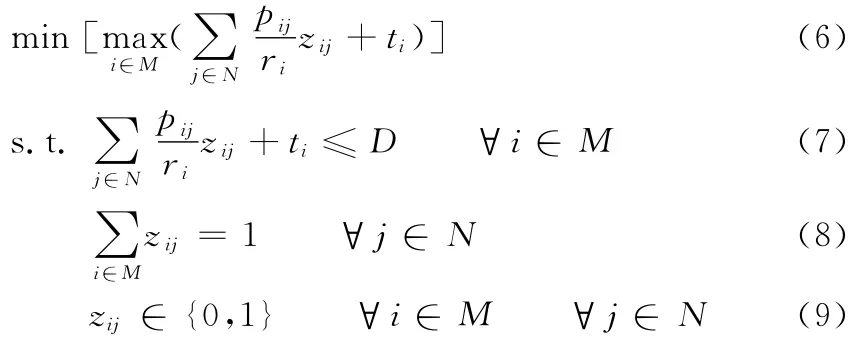
其中，式（6）是目标函数，用于寻找在所有可行订单分配方案中完成所有工件加工所需时间最短的订单分配方案；约束式（7）表示每个工厂必须在交货期限前完成工件的加工；约束式（8）表示每个工件的加工需求均要得到满足，且只能分配给一个工厂。

3.2 生产运输集成调度问题模型

经过订单分配，工厂i需要加工的工件集合记为Ni。每个工厂i对生产和运输进行集成调度，以实现交货期限内完成Ni中所有工件的生产运输总成本最小化。生产运输集成调度的决策变量与1.2节中模型的决策变量相同。每个工厂i的生产运输集成调度问题模型为

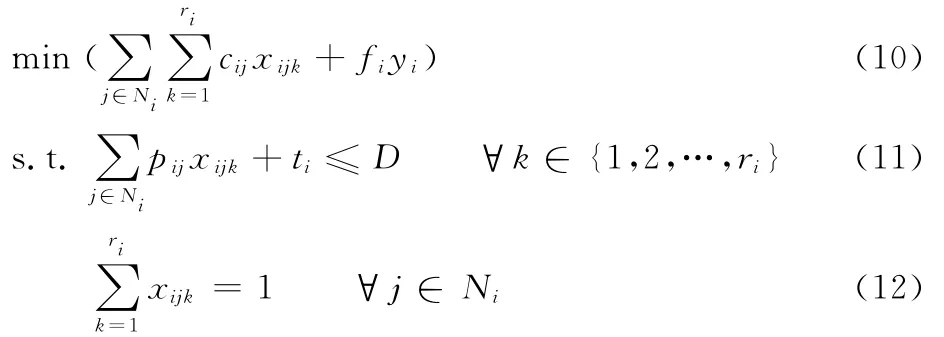
其中，式（10）是目标函数，为工厂i的生产和运输总成本最小化；约束式（11）表示工厂i的每台机器加工的工件必须在交货期限内完成；约束式（12）表示分配给工厂i的每个工件的加工需求均要得到满足，且只能由工厂i的一台机器加工；约束式（13）为对工厂i发送批次的约束。

4 仿真实验及分析

4.1 算例

10个零部件加工厂为总装工厂提供500个工件，每个运输批次最多可发送6个工件，交货期限为1200。为了避免具体算例对算法性能可信度的影响，本文通过随机方式生成以下数据，每个零部件加工厂拥有的机器数服从均匀分布［2，5］，各零部件加工厂到总装工厂的运输时间和运输成本均服从均匀分布［100，1000］，工件在各零部件加工厂的加工时间服从均匀分布［10，100］，加工成本服从均匀分布［100，500］。

4.2 结果及分析

为了验证平行机多工厂供应链调度策略优于独立决策策略，本文对2种不同策略进行比较，2种策略均使用CPLEX 12.2求解。同时为了验证本文禁忌算法的有效性，本文分别使用本文禁忌算法和CPLEX 12.2对算例进行求解。本文禁忌算法通过Visual C＋＋2005实现，并使用C＋＋标准模板库。PC为 AMD Athlon（tm）Ⅱ X2 245，4GB RAM。表1为本文禁忌算法的参数设置。

表1 参数设置

针对10组随机算例，分别运算10次。2种不同决策的比较结果如表2所示，2种不同求解方法的比较结果如表3所示。

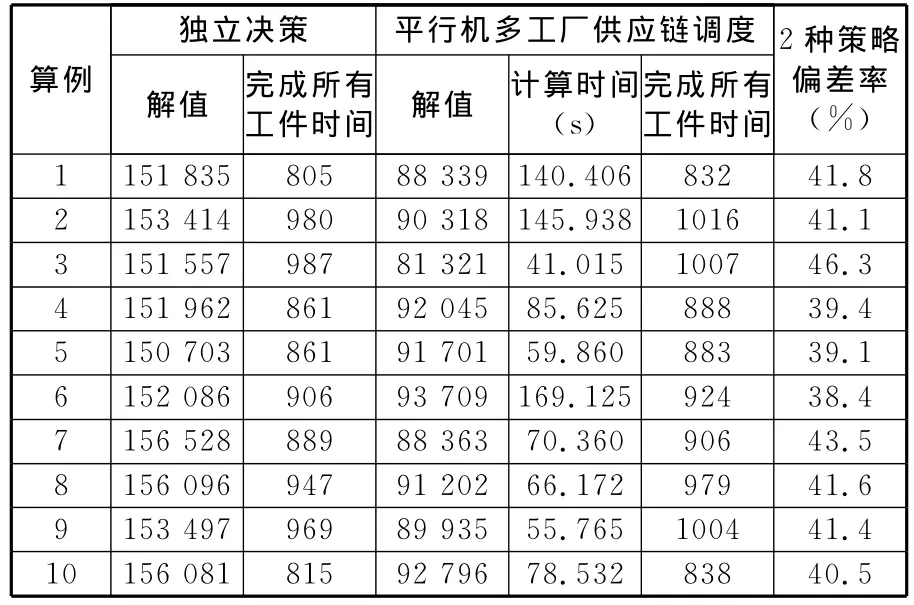
表2 2种不同决策策略的比较结果

表3 两种不同求解方法的比较结果

由表2可知，平行机多工厂供应链调度策略完成所有工件花费的时间仅比独立决策多约26，但生产运输总成本却降低了40%左右。原因为：独立决策时各部门的决策目标不一致，导致了企业的整体利益的损失。供应链调度决策在交货期限允许的情况下，以延长较短的交货时间为代价，大幅度地降低了供应链的运作成本，体现了平行机多工厂供应链调度策略的优越性。

由表3可知，本文禁忌算法得到的平均结果与CPLEX得到的最优解的偏差仅约3%，但却节省了90%以上的运算时间。同时，CPLEX对10个不同算例的计算时间差异较大，标准差为44.09，而本文禁忌算法的平均计算时间标准差仅为0.34。因此，本文禁忌算法能够在较短且稳定的时间内得到满意的结果。

5 结论

（1）本文针对大型装备制造企业内部供应链的特点，提出了一类平行机多工厂供应链调度问题，给出了解的最优性条件，并建立了问题的数学模型。

（2）根据解的特点，提出了一种向量组编码结构，并设计了禁忌搜索算法及块结构、插入、交换3种邻域操作。

（3）通过仿真实验验证了平行机多工厂供应链调度策略的优越性和本文禁忌算法的有效性。

［1］柏孟卓，陈峰，唐国春.供应链管理中生产和运输集成的排序问题［J］.工业工程与管理，2007，12（5）：47－50.

［2］Hall N G，Potts C N.Supply Chain Scheduling：Batching and Delivery［J］.Operations Research，2003，51（4）：566－584.

［3］Hall N G，Potts C N.The Coordination of Scheduling and Batch Deliveries［J］.Annual of Operations Research，2005，135（1）：41－64.

［4］Averbak I，Xue Zhihui.On－line Supply Chain Scheduling Problems with Preemption［J］.European Journal of Operational Research，2007，181（1）：500－504.

［5］Pundoor G，Chen Zhilong.Scheduling a Production－distribution System to Optimize the Tradeoff between Delivery Tardiness and Total Distribution Cost［J］.Naval Research Logistics，2005，52（6）：571－589.

［6］Chen Zhilong，Pundoor G.Integrated Order Scheduling and Packing［J］.Production and Operations Management，2009，18（6）：672－692.

［7］Chen Zhilong，Vairaktarakis G L.Integrated Scheduling of Production and Distribution Operations［J］.Management Science，2005，51（4）：614－628.

［8］陈荣军，唐国春.平行机的供应链排序［J］.系统科学与数学，2010，30（2）：274－282.

［9］Chen Zhilong，Pundoor G.Order Assignment and Scheduling in a Supply Chain［J］.Operations Research，2006，54（3）：555－572.

［10］蒋大奎，李波.基于混合禁忌搜索算法的供应链排序问题［J］.机械工程学报，2011，47（20）：53－59.

［11］Chen Zhilong.Integrated Production and Outbound Distribution Sheduling：Review and Extensions［J］.Operations Research，2010，58（1）：130－148.

［12］Armentano V A，Shiguemoto A L，Lokketangen A.Tabu Search with Path Relinking for an Integrated Production－ distribution Problem ［J］.Computers ＆ Operations Research，2011，38（8）：1199－1209.

［13］潘全科，朱剑英.一类解决Job shop问题的禁忌搜索算法［J］.中国机械工程，2006，17（5）：536－539.

［14］Nowicki E，Smutanicki C.A Fast Taboo Search Algorithm for the Job－shop Problem［J］.Management Science，1996，42（6）：797－813.