锻锤振动系统参数对振动响应影响的仿真分析

刘 欢，陈长征，周 勃，周 昊

(1.沈阳工业大学 机械工程学院，辽宁 沈阳 110870;2.沈阳化工大学 信息工程学院，辽宁 沈阳 110142;3.沈阳工业大学 建筑工程学院，辽宁 沈阳 110870)

1 引言

当前专家们长期致力于锻压设备减振和隔振等技术的研究。同时，寻找最简便和最经济的减振和隔振方案，改善车间工作环境，减少振动和噪音给工人和机器设备带来的危害，有着重要的现实意义。通过对仿真结果的研究，从而分析不同因素对振动特性的影响。同时再经过复杂的计算，进而验证仿真模型的可靠性［1］。

2 力学模型建立

在锻锤操作过程中，土壤和锻锤中的弹性垫层的阻尼作用是一直存在的。综合考虑现场施工的各方面因素，有无阻尼之间的计算结果，相差一半左右。因此，在计算锻锤产生的基础振动中，必须考虑阻尼的影响［2］。

对双自由度有阻尼振动力学模型，提出以下设想:刚性整体是由砧座m1和基础m2组成，用于支承砧座的隔振器是线性弹性体k1和k2的组合，支承基础的土壤是粘性阻尼为c1和c2之间的组合，打击力通过底面形心、基础的重心和砧座进行传递，进行打击后系统开始做自由振动，力学模型如图1所示。

可得出下面的振动方程:

式中，c1和c2分别为砧下垫层和地基的阻尼。方程 (1)的初始条件为式 (2)。

图1 双自由度有阻尼力学模型Fig.1 Two degrees of freedom dynamic model with damping

相对来说振动方程 (1)所描述的锻锤基础振动更贴近于实际，因此对振动方程 (1)与初始条件式 (2)进行计算，所得出的振动参数值将更加精确。

3 振动系统参数分析及仿真验证

3.1 锻锤振动系统各参数对振动响应影响

由于影响基础振动的因素较多，根据锻锤的运动方程，分别以基础质量m2为变量，地基土的阻尼c2、刚度k2，砧下垫层的阻尼c1、刚度k1，以上这些系统参数对于砧座基础振动，振动和地基所受的影响进行分析［3-4］。已知:m1=16 E+3;m2=160 E+3;k1=2.14 E+7;k2=8.66 E+8;v1=0.55 m/s;c1=1.053 E+6;c2=3.16 E+6

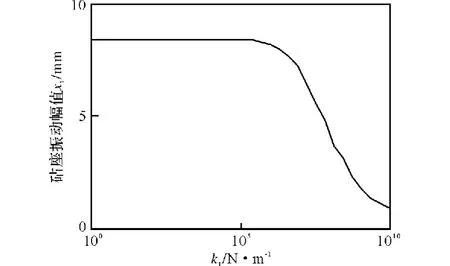
图2 砧座振动位移曲线Fig.2 Vibration displacement curve of anvil stand

图3 基础振动位移曲线Fig.3 Vibration displacement curve of foundation

图4 地基受力幅值曲线Fig.4 Stress amplitude curve of foundation

已知:k1=9.92 E+8;k2=8.66 E+8;c1=1.05 E+7;c2=3.16 E+7;m1=16 E+3;v1=0.55 m/s;通过Matab仿真得到图5～图7。

从图2～图7的曲线结果可知，砧座垫层的刚度系数k1对系统的基础振动影响较大。当砧座垫层的刚度系数k1增大时，砧座的最大位移减小，而基础的最大位移和地基承受的最大动荷载增大明显。当增大砧座垫层阻尼c1时，砧座的位移减小，而基础最大位移和地基承受动荷载也有略微的减小。因此，在c1和k1两个参数中，k1对系统的基础减振起重要作用，而c1是对加快衰减起重要作用的。

图5 砧座振动位移曲线Fig.5 Vibration displacement curve of anvil stand

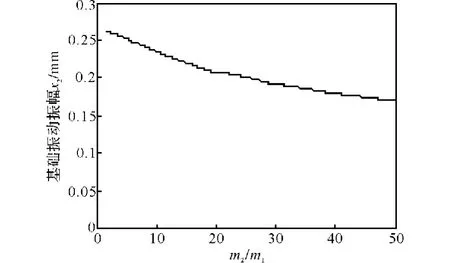
图6 基础振动位移曲线Fig.6 Vibration displacement curve of foundation

阻尼对于振动持续时间来说是起关键作用的。增大地基的刚度系数k2，基础的最大位移减低显著，而地基承受动荷载增加较少。在砧座的质量m1恒定的条件下，增大m2就会增加基础减振效果，但m2增加过大又不经济，因此，在锻锤基础改造操作时，应该综合各方面的因素考虑，从改变砧座垫层阻尼和刚度系数入手。系统参数对振动的影响见表1。

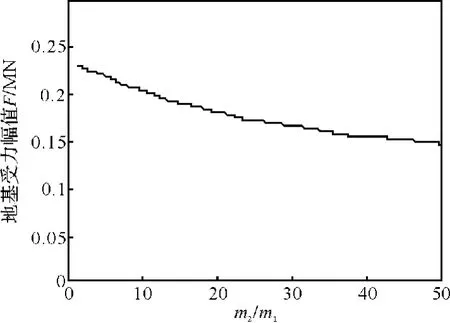
图7 地基受力幅值曲线Fig.7 Stress amplitude curve of foundation

表1 系统参数对振动的影响Tab.1 Influence of each parameter on vibration isolation system of hammer foundation

3.2 仿真验证

在进行仿真验证时，利用Matlab软件计算仿真结果。在有限点内进行求解［5-6］。在所求出的解变化较快时，在区间内使用较多的点求解，当所求的解变化较平滑时，在区间内使用的点数较小一些。

为了说明该仿真模型的可靠性，本文特别对文献［7］中的算例进行了进一步的计算，砧座和基础位移曲线与原文献［7］基本一致。并与其计算结果对比见表2。原文献［7］对3t锻锤隔振系统进行了动态仿真。设计参数为k1=4.75×107N/m;k2=9.6687×109N/m;m1=98 300 kg;m2=537 000 kg;c1=1213 777 kg/s;c2=34587 027 kg/s;μ=0.24;v0=6.7 m/s。通过 Matlab仿真分别得到图8～图9。

图8和图9为仿真的结果图。通过表2结果可知，仿真模型的计算结果与原文献 ［7］中的仿真结果一致，充分的显示出该仿真模型具有良好的可靠性。

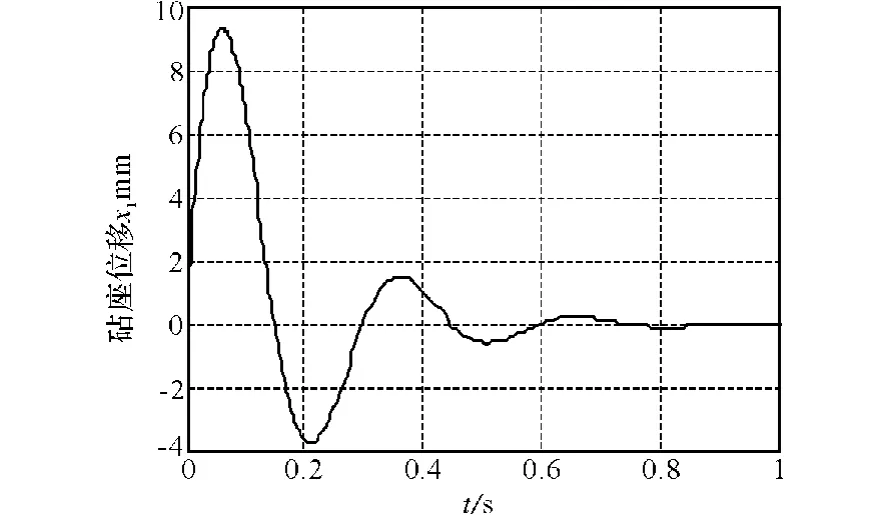
图8 砧座位移仿真曲线Fig.8 Simulation curve for displacement of anvil stand

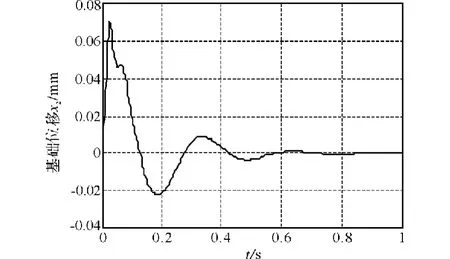
图9 基础位移仿真曲线Fig.9 Simulation curve for displacement of foundation

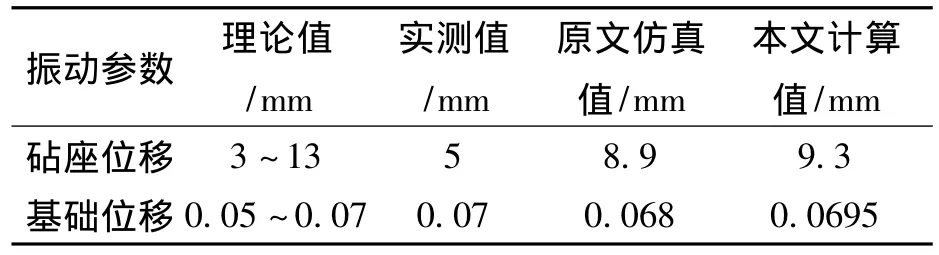
表2 振动参数理论值、实测值、原文仿真值和本文计算值比较Tab.2 Comparison among theoretical values，measured values，original and textual simulation values of vibration parameters

4 结语

经过对振动系统中影响振动响应的参数进行仿真，包括内基础与砧座质量比以及参数k1和k2，并分析出系统中各参数对振动的影响。仿真结果表明，该仿真模型具有较好的可靠性，可用来优化系统模型和技术参数，并对锻锤在工程设计中的应用具有较好的指导作用。

［1］陈维民，曹喜滨，高乃光，等.锻锤的振动分析及砧下直接减振研究 ［J］.机械工程学报，2009，28(1):36－41.

［2］阙礼生，何成宏，杨国泰.3t模锻锤板簧悬挂式隔振装置的施工与安装 ［J］.锻压机械，2009，25(4):47－49.

［3］林远东.偏心质量引起旋转系统振动的动力学研究 ［J］.机械设计与制造.2008，25(4):37－39.

［4］张我华，任廷鸿，邱战洪.锻锤基础的冲击疲劳损伤分析 ［J］.振动工程学报，2008，18(4):506－511.

［5］杨鑫.锻锤基础振动控制的研究 ［D］.沈阳工业大学硕士学位论文，2009.

［6］张银娟，刘军，王永科.基于虚拟样机技术的液压模锻锤动态仿真研究 ［J］.煤矿机械，2010，3(4):85－87.

［7］辛勇，何成宏，杨国泰，等.隔振锻锤的数值仿真［J］.塑性工程学报，2007，12(4):38－41.