基于对立统一定理的灌区旱情等级评价

潘建波，王文川，徐冬梅

（1.华北水利水电学院 土木与交通学院，河南 郑州450011；2.华北水利水电学院 水利学院，河南 郑州450011）

0 引言

中国是农业大国，农业旱灾是农业生产的重大威胁.根据国家防汛抗旱总指挥部的统计，1979—2008年间，中国平均每年农作物因旱受灾面积2.56×107h m2，成灾10.29×107h m2，因旱造成粮食损失244.6亿kg，约占全年粮食总产量的5.7%［1］.特别是近几年，中国旱情有加重的趋势，从2008年11月下旬开始，中国冬麦区降水量明显偏少，旱情持续发展，加之入冬后几次强降温天气过程造成旱冻交加，对冬小麦安全越冬正常发育造成严重影响.这次干旱持续时间之长、受旱范围之广、受旱程度之重为历史罕见.截至2009年2月3日，灾害已经让全国近43%的小麦产区受旱.河南、安徽、山东、河北、山西、陕西、甘肃等7个主产区小麦受旱9.53×106h m2，比上年同期增加8.93×106h m2.其中，严重受旱3.79×106h m2，比上年同期增加3.74×106h m2.2010年大旱导致西南五省区市除四川之外，至少有218万人返贫，经济损失超350亿元.冬麦区大部自2010年10月以来累计降水量不足25 mm，比多年同期偏少5至9成，截至2011年1月28日，全国作物受旱面积5.16×106h m2，257万人、279万头大牲畜因旱出现饮水困难，仅山东、河南两省受旱面积就达3.06×106h m2，占全国受旱面积的59%.因此，如何及时制定有效的抗旱减灾方案，合理地进行灌区抗旱工作，这就需要对某一自然条件和工程条件下的灌区旱情程度进行客观的评价和分析.因此探讨合理有效地旱情等级评价方法，确定其旱情等级，对管理部门抗旱救灾具有重要的指导意义.

目前，国内外关于灌区干旱的研究多集中在干旱指标的选取上［2］，而对评价的方法则较少涉及［3］.常用的灌区干旱评价方法多为单指标评价法，如降雨频率法、降雨随机模拟法、干湿系数法、干燥度法、降雨距平法及干旱指数法等，多指标的有模糊综合评价法和可拓评价法［3－5］.模糊综合评价是利用最大隶属度原则确定分级，在模糊概念分级条件下，最大隶属度原则易导致信息丢失而引起判别结果出现偏差［6］.作者基于对立统一定理，建立了灌区旱情等级评价的可变模糊评价新方法，模型能综合考虑评价系统的线性特征和非线性特征，在具体应用时，可根据问题的实际情况和问题本身的性质进行确定，进一步提高评价结果的可靠性.

1 基于可变模糊集理论的对立统一定理

可变模糊集理论是陈守煜教授于2005年建立，并于2010年提出对立统一定理［6－7］，为了论述方便，本文作一简介.

设论域U中的任意元素u的对立模糊概念（事物、现象）或u对立的基本模糊属性，以A～与表示.在参考连续统区间［1，0］（对）与［0，的任一点上，对立模糊属性的相对隶属度分别为且

～

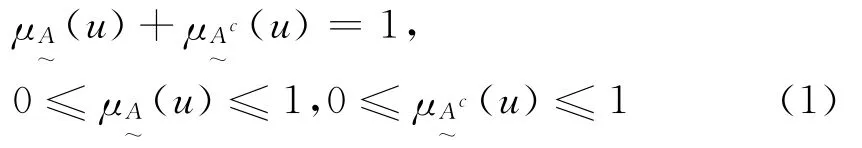
～在pl和pr之间必定存在中介点pm，如图1所示，该点的对立模糊概念（事物、现象）或对立基本模糊属性的相对隶属度相等，即则pm为连续统区间［1，0］（对的渐变式质变点.因为从pl点变化到pr点，其间必定经过0.5的中介点pm.由于所以Pm同时具有.在线段在线段pmpr间则中介 点 pm必 为 连 续 统 区 间 ［1，0］（对的渐变式质变点，即对立统一矛盾性质的渐变式转化点.

图1 对立统一定理的连续统示意图Fig.1 The continuum sketch map of theorem of unity of opposites

2 基于对立统一定理的灌区农业旱情等级评价新方法

2.1 计算待评灌区农业对象u对旱情等级h的指标相对隶属度

设待评灌区对象u，根据已知的多个级别h（h＝1，2，…，c.为级别总数），多个指标（i＝1，2，…，m，为评价指数总数）的指标标准区间矩阵可表示为

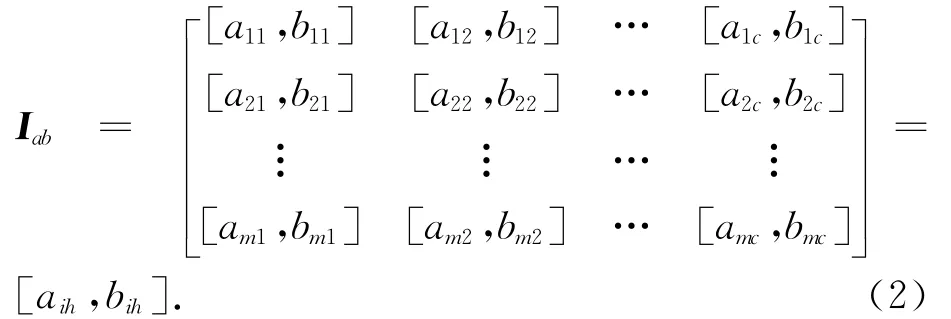
式中：i＝1，2，…，m；h＝1，2，…，c.并设定1级干旱程度强于2级，2级干旱程度强于3级，c级最弱.

在实际干旱程度定量分析中指标标准值区间［aih，bih］有两种情况：①aih＜bih，称递增系列，其指标特征值越大，干旱程度越强；②aih＞bih，称递减系列，其指标特征值越小，干旱程度越强.

根据实际情况的物理概念分析可知，在已知级别h指标i特征值的相对隶属度为1的矩阵：

的条件下，位于Mih与Mih＋（）1的指标特征值ui，对级别h与（h＋1）构成相对的对立模糊概念，根据对立统一定理有

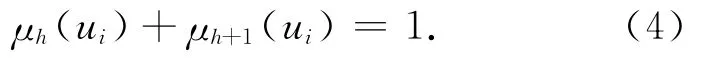
式中：μh（ui）、μh＋1（ui）分别为待评对象u指标i对级别h与（h＋1）的相对隶属度.

设待评灌区对象u指标i的特征值ui落入h与（h＋1）级相对隶属度为1的M矩阵的区间［Mih，Mi（h＋1）］内，则ui对h 级的相对隶属度为

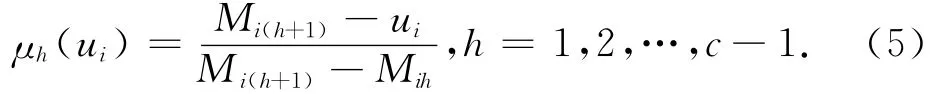
当ui＝Mih时，μh（ui）＝1，由式（3）μh＋1（ui）＝0；当ui＝Mi（h＋1）时，μh（ui）＝0，由式（4）μh＋1（ui）＝1；当ui＝ （Mih＋Mi（h＋1））／2时，μh（ui）＝0.5，由式（4）μh＋1（ui）＝0.5.所以，应用式（4）和式（5）可以计算待评对象u指标i的特征值ui对级别h与h＋1的相对隶属度.显然，对于小于h，大于（h＋1）的指标i的相对隶属度均等于零.

2.2 计算待评灌区农业对象u对旱情等级h的综合相对隶属度

根据式（5）和式（4）计算得到的相对隶属度μh（ui）、μh＋1（ui）是指标i对级别h 的单指标相对隶属度.灌区旱情等级评价是多指标综合评价问题，指标具有不同的权重.设已知指标权重向量为

式中：p为距离参数；p＝1为海明距离；p＝2为欧式距离.

若待评灌区对象u对级别h的多指标综合相对隶属度以v（u）表示，则其算式为［7］

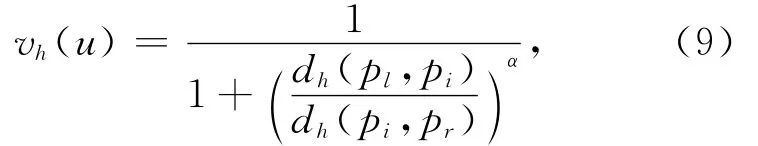
式中：α为优化准则参数；α＝1为最小一乘方优化准则；α＝2为最小二乘方优化准则.式（10）满足：

（1）当pi与pl重合时，μh（ui）＝1，dh（pl，pi）＝0，则vh（u）＝1，vh＋1（u）＝0；

（2）当pi与pr重合时，μh＋1（ui）＝1，dh（pi，pr）＝0，则vh（u）＝0，vh＋1（u）＝1；

（3）当pi与pm重合时，μh（ui）＝μh＋1（ui）＝0.5，dh（pl，pi）＝dh（pi，pr），则vh（u）＝vh＋1（u）＝0.5；

（4）当pi位于区段plpm时，有dh（pl，pi）＜dh（pi，pr），则vh（u）＞vh＋1（u）；

（5）当pi位于区段pmpr时，有dh（pl，pi）＞dh（pi，pr），则vh（u）＜vh＋1（u）；

因此，式（8）满足对立统一定理，用于计算待评灌区对象u对级别h的相对隶属度.

若采用优化准则参数α＝1，距离参数p＝1，则式（9）变为

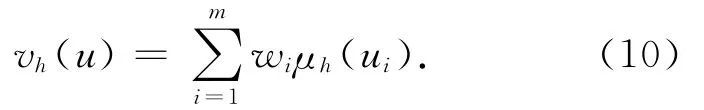
式（9）是一个线性公式.如果考虑灌区综合评价为非线性系统，可采用p＝2即欧氏距离，式（9）变为

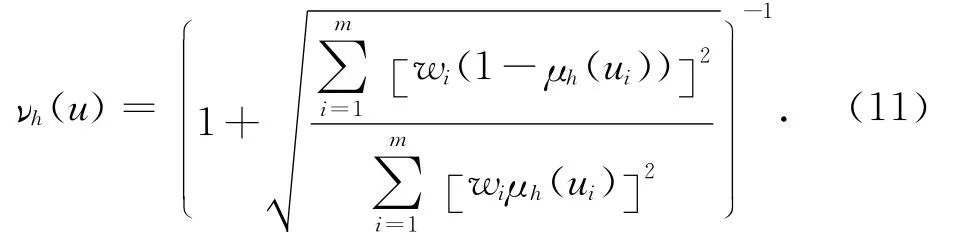
这是一个非线性公式.因此综合评价模型（9），只要改变距离参数p，既可用于线性系统评价，也可用于非线性系统评价.

当α＝2时，无论p＝1还是p＝2，式（9）都是非线性公式.考虑到α＝2对距离比值dh（pl，pi）／dh（pi，pr）具有放大或缩小效应，所以在综合评价中宜采用α＝1.所以，可变模糊综合评价模型式（9）在数学上满足对立统一定理，说明它在哲学上符合唯物辩证法的对立统一规律.既可以评价线性的系统又可以评价非线性的系统.这是该模型的特点和优点.

根据文献［8］的级别特征值公式，可计算待评灌区的旱情级别特征值

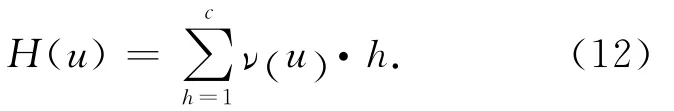
3 应用实例

关中西部四大灌区位于陕西省关中渭河平原西部，由冯家山灌区、宝鸡峡灌区、羊毛湾灌区和石头河灌区组成，涉及西安、咸阳、宝鸡三个市，是陕西省主要的粮食、果林、油料、和蔬菜产地之一.关中地区属于干旱和半干旱气候带，水资源匮乏，加上本区内蓄水工程少，水资源调蓄能力差，供水保证率低，旱灾出现频繁.探讨合理有效地旱情等级评价方法，确定其旱情等级，对管理部门抗旱救灾具有重要的指导意义.为验证本文方法的可行性和有效性，引用文献［3］中的数据，选取降雨指标、径流指标、水库蓄水指标、地下水指标为评价指标.划为重度干旱、中度干旱、轻度干旱、不发生干旱4个等级表述灌区干旱程度［9］.灌区旱情等级划分标准如表1所示，关中地区四大灌区评价因素指标值如表2所示.

表1 灌区旱情等级划分标准Tab.1 The division standard of drought grade of irrigation district

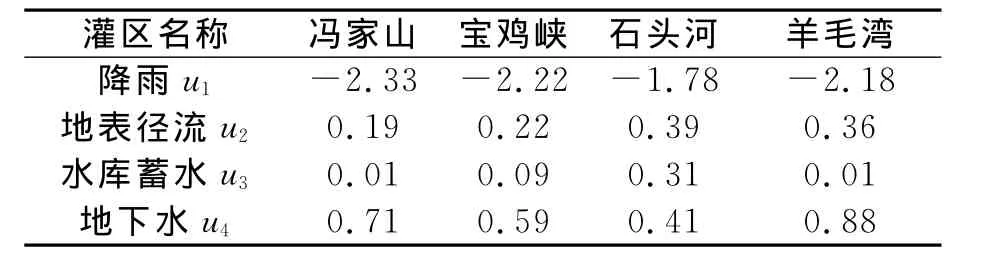
表2 关中地区四大灌区评价因素指标值Tab.2 The index value of evaluation f actor of for irrigation district in Guanzhong area

根据表1、2可得关中地区四大灌区的旱情等级划分标准区间矩阵和评价因素指标特征值矩阵：

根据文献［7］Mih与aih、bih的关系式可以为

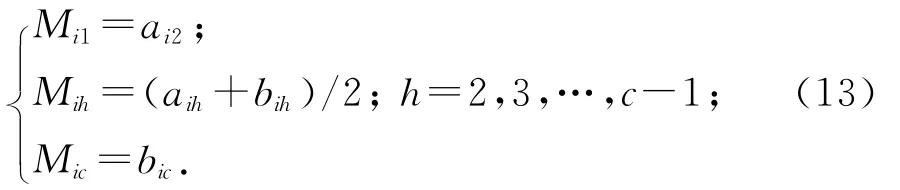
根据式（12）可得级别h指标i特征值的相对隶属度等于1的矩阵：

根据评价因素指标特征值矩阵X可知冯家山地下水指标u4＝71，指标（4）落入指标相对隶属度等于1的矩阵M的1、2级之间，即落入区间［M41，M42］＝［0.70，0.75］.应用公式（5），i＝1，h＝1，得μ1（u4）＝（0.75－0.71）／（0.75－0.70）＝0.8，由对立统一定理公式（4）μ2（u4）＝0.2.根据对立统一定理，小于h大于（h＋1）级的指标相对隶属度为0，即μ3（u4）＝0、μ4（u4）＝0.则得冯家山地下水指标u4的相对隶属度向量为μ⇀（u4）＝（0.8，0.2，0，0）.类似可得到冯家山干旱指标ui（i＝1，2，3，4，）对级别h（h＝1，2，3，4）的相对隶属度矩阵为

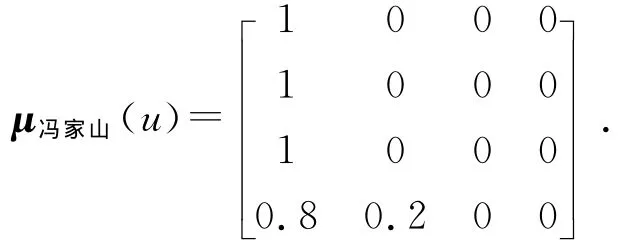
为了与文献［4］进行对比分析，采用文献［4］给出的4个灌区的评价指标权重向量.

应用可变模糊综合模型公式（9），可求得冯家山对级别h（h＝1，2，3，4）的线性和非线性的综合相对隶属度，见表3，同理也可求出宝鸡峡、石头河和羊毛湾灌区的线性和非线性的综合相对隶属度，其结果如表3所示.根据级别特征值公式（12），可计算灌区旱情等级的线性和非线性模型的级别特征值见表3.

表3 线性和非线性模型的综合相对隶属度及级别特征值Tab.3 The comprehensive relative membership degree and grade characteristic value of linear and nonlinear model

4 结果分析与讨论

根据表3中线性评价模型和非线性评价模型的级别特征值，可得出冯家山、宝鸡峡、石头河和羊毛湾灌区的综合平均级别特征值分别为1.045、1、1.2、1.47.评价4个灌区均属于1级，即重度干旱.但重度干旱的强弱有所不同，宝鸡峡最强，冯家山次之，羊毛湾最弱.文献［3］采用非对称贴近度原则评价旱情等级，冯家山、宝鸡峡、石头河和羊毛湾灌区的等级变量特征值分别为3.6282，3.5985，3.5294，3.6237，评价4个灌区均属于重度干旱与本文相同.但从给出的级别特征值来看，其重度干旱的强弱排序应该为冯家山、羊毛湾、宝鸡峡、石头河，与本文不同.结合表1、2中数据进行分析可知，冯家山有一项指标地下水u4＝0.71属于中度干旱，但非常接近重度干旱的指标0.70，其它三项指标属于重度干旱；宝鸡峡的4项干旱指标特征值全部属于重度干旱；石头河有一项指标水库蓄水u3＝0.31属于中度干旱，但接近中度干旱区间［0.20，0.50］中间值，其它三项指标属于重度干旱；羊毛湾有一项指标地下水u4＝0.88属于轻度干旱，其它三项指标属于重度干旱.因此，宝鸡峡应该是重度干旱的强度最大，羊毛湾重度干旱的强度最小，与本文量化分析的结果一致，说明本文的计算结果更符合实际情况.

5 结束语

作者基于可变模糊集理论的对立统一定理，建立了灌区旱情等级评价的可变模糊评价新方法，提出的方法满足唯物辩证法的对立统一规律，理论严谨，概念清晰，计算简便.模型综合考虑灌区旱情评价系统的线性特征和非线性特征，均衡了两者之间的差异，令结果更具说服力和可靠性.实例应用结果表明，该方法不但能准确给出旱情的等级，而且能清楚地给出其强弱排序，这对进行抗旱的先后顺序具有重要的指导意义.与文献［4］和实际情况的对比分析，说明了本文的计算结果更符合实际情况.

［1］ 水利部办公厅，水利部发展研究中心.水利改革发展30年回顾与展望［M］.北京：中国水利水电出版社.2010.

［2］ 王晓红，胡铁松，吴凤燕，等.灌区农业干旱评估指标分析及应用［J］.中国农村水利水电，2003（7）：4－6.

［3］ 孙廷容，黄强，张洪波，等.基于粗集权重的改进可拓评价方法在灌区干旱评价中的应用［J］.农业工程学报，2006，22（4）：70－74.

［4］ 刘晓宁，贾忠华.模糊综合评价在关中灌区干旱评价中的应用［J］.水资源与水工程学报，2005，16（2）：62－66.

［5］ 王斌，付强，王忠波，等.基于降水随机模拟的旱作区农业旱情等级划分方法［J］.中国农村水利水电，2011（3）：167－170.

［6］ 陈守煜.可变模糊集理论与模型及其应用［M］.大连：大连理工大学出版社，2009.

［7］ 陈守煜.基于可变模糊集的辩证法三大规律数学定理及其应用［J］.大连理工大学学报，2010，50（5）：838－844.

［8］ 陈守煜.工程模糊集理论与应用［M］.北京：国防工业出版社，1998.

［9］ 成福云.关中灌区干旱指标体系的建立与抗旱措施研究［D］.西安：西安理工大学水利水电学院，2003.