基于改进欧几里德算法的(n,1,m)卷积码识别
2012-12-01刘建成杨晓静
刘建成,杨晓静,张 玉
(解放军电子工程学院,安徽 合肥 230037)
0 引言
在数字通信中,信道编码包括线性分组码、卷积码、LDPC码和Turbo码等。卷积码因纠错能力强、编译简单,广泛应用于卫星系统测控链路、深空探测系统和第三代移动通信中,这使得卷积码的识别成为信息截获领域中急需解决的问题。目前,针对卷积码的识别主要有高斯消元法、基于快速双合冲算法、构建分析矩阵法和欧几里德算法。在低码率卷积码识别中,高斯消元法运算量大,复杂度为O(N3),其中N为方程组未知数的个数一般大于22;传统欧几里德算法[1]和基于快速双合冲算法[2]均只适用于(2,1,m)卷积码,计算复杂度分别为O(L2/4)、O(L2),L为所需码字序列长度一般不小于25;构建分析矩阵法[3]需要几千比特的数据量,对矩阵化简的运算量大于高斯消元法。可见,对(n,1,m)卷积码识别的现有方法主要有两点不足:1)应用范围受限,不能对所有(n,1,m)进行识别;2)所需数据量大,运算较复杂。本文提出的改进欧几里德算法可有效弥补这两点不足。
1 (n,1,m)卷积码识别问题数学描述
本文讨论卷积码是建立在二元域F2上,一般表示为(n,k,m),其中n为码长,k为信息位,m 为记忆长度。(n,k,m)卷积码的编码过程可用F2上的多项式矩阵表示为[4]:
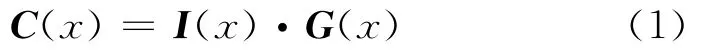
式(1)中,C(x)为(1×n)的码字多项式矩阵、I(x)为(1×k)的信息多项式矩阵、G(x)为(k×n)的生成多项式矩阵。(n,1,m)卷积码编码可表示为:
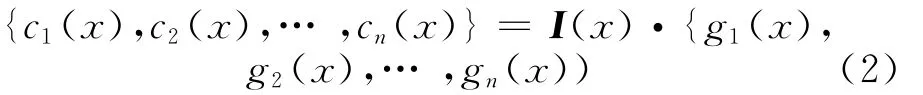
ci(x)和gi(x)分别为子码多项式和子生成多项式,i=1,2,…,n。
对(n,1,m)卷积码的识别问题就是在仅知C(x)= {c1(x),c2(x),…,cn(x)}的情况下如何求出 G(x)= {g1(x),g2(x),…,gn(x)},进 而 得 出I(x)实现对信息的恢复。对式(2)展开得:

即,

可 见,I(x)为c1(x),c2(x),…,cn(x)的 公 因式。由文献[4]可知,为了避免恶性码的产生,其生成多项式需满足:g1(x),g2(x),…,gn(x)的最高公因式为xL,0≤L<m,m为记忆长度(即gi(x)的最高幂次)。又因I(x)为输入信息序列的多项式,实际中幂次大于m,所以I(x)即为c1(x),c2(x),…,cn(x)的最高公因式,在文献[5]中表示为:
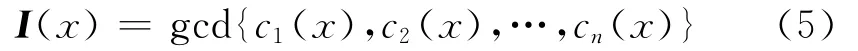
式(5)中,gcd(·)表示求解最大公约数和最高公因式。在仅知c1(x),c2(x),…,cn(x)的情况下求出I(x),即可得g1(x),g2(x),…,gn(x)。这样,(n,1,m)卷积码的识别问题就转化为求已知码字多项式c1(x),c2(x),…,cn(x)的最高公因式。
欧几里德算法是计算两个数最大公约数的算法,又名辗转相除法,可用于求解Fq(x)上两个多项式a(x)和b(x)的最高公因式。辗转相除过程如下:

式(6)中,deg(·)表示最高幂次,当余数多项式ri(x)等于0时,余数多项式ri-1(x)=gcd{a(x),b(x)}。欧几里德算法只适用于求解两个多项式最高公因式,下文将对其进行改进,求解n个多项式最高公因式。
2 欧几里德算法的改进及应用
2.1 欧几里德算法的改进
定理[5]1:设a和b是两个整数,而b≠0。那么存在唯一的一对整数q和r,使得

式(7)中,|b|表示b的绝对值。
定理[5]2(算术基本定理):任何大于1的整数都可以表示成一些素数的乘积,如果不计这些素数在乘积中排列的先后顺序,那么这种表示法是唯一的。
利用上述定理,经典的欧几里德算法只用于求两个正整数的最大公约数,本文对该算法进行推广,使其可求n个正整数的最大公约数。
设{a1,a2,…,an}为n个正整数,利用改进的欧几里德算法求解最大公约数,具体步骤如下:
1)取r0,k= min{ak,1≤k≤n},其余n-1个{ai}按原顺序编为{r0,1,r0,2,…,r0,n-1},由定理1可知r0,i∈ {r0,1,r0,2,…,r0,n-1}均可唯一表示为:

2)同步骤1),再由n-1个r得出r1,k=min{r1,i|r1,i≠0,1≤i≤n-j},同时找出r1,i=0,记个数为m1,对n-m1-2个r1,i∈ {r1,i|r1,i≠r1,k,0}重新编号为r1,1,r1,2,…,r1,n-m-2。此时r1,i可表示为:
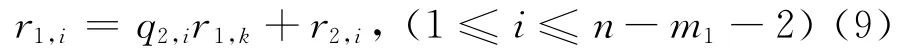
3)对 {rj,i}重复步骤2),直至n-m1-…-mj-j-1=2,设此时j=m,则定义rm,1和rm,2为{a1,a2,…,an}的剩余项。
4)利用经典欧几里德算法求步骤3)中剩余项{rm,1,rm,2}的最大公约数,gcd(rm,1,rm,2)=dm,r。
5)j从m 到1,初始化dj,r=dm,r。依次验证dj,r是否能整除rj-1,k,即是否满足rj-1,kmod(dj,r)=0。若满足则dj-1,r= dj,r,否则 dj-1,r= gcd(dj,r,rj-1,k)。
6)得{a1,a2,…,an}的最大公约数,gcd{a1,a2,…,an}=d0,r。
2.2 算法的计算复杂度分析
对于求解n 个整数{a1,a2,…,an}最大公约数的问题,一般采用先求 gcd(a1,a2)=d1,再求gcd(d1,a3)=d2,依次类推至gcd(dn-2,an)=dn-1,共需要进行n-1次最大公约数求解。改进的算法在最坏(即式n-m1-…-mj-j-1中的mk(1≤k≤j)均为0,步骤5)中rj-1,kmod(dj,r)=0均不满足)的情况下,才需进行n-1次欧几里德求最大公约数计算。所以本文提出的算法一般只需要N=n-(Nm+Nj+1)次欧几里德最大公约数计算,其中Nm= m1+m2+ … +mj,Nj为步骤5)中rj-1,kmod(dj,r)= 0 的 次 数, 算 法 复 杂 度 为O(L2/2n)。而在同等条件下,构建分析矩阵法复杂度为O(L3),L为码字序列长度(一般不小于12n)。可见,该算法在解决应用范围受限问题的同时与构建分析矩阵法相比有效地降低了算法复杂度。
2.3 算法的应用
由文献[5]第十章可知,解决有限域上两个多项式的最高公因式求解问题可采用与求两个数的最大公因式一样的欧几里德算法(又称辗转相除法)。同样,本文对欧几里德算法的改进也可用于对n个二元域F2上多项式{f1(x),f2(x),…,fn(x)}最高公因式的求解,即可用于解决对(n,1,m)卷积码的识别。由于实际中所截获的码元序列不能构成完整的码字多项式,本文利用参考文献[1]中的修饰算法可实现对式(4)和(5)的求解。设c1(x),c2(x),…,cn(x)分别为所获取的n个(n,1,m)卷积码的不完整码字,对g1(x),g2(x),…,gn(x)识别的具体步骤如下:
1)假设记忆长度为L,选取c1(x),c2(x),…,cn(x)中次数最低的一个码字记为:
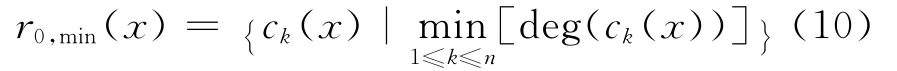
将其余码字记为:
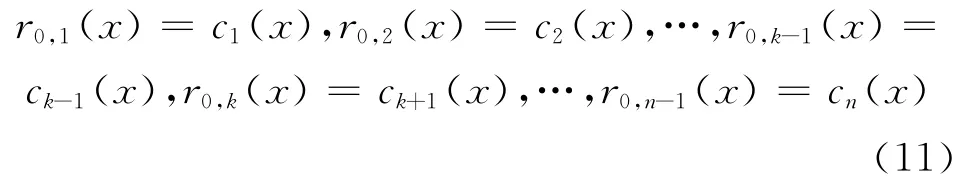
2)对j≥0,定义多项式集合为{qj,i(x)}和{rj,i(x)},它们满足以下关系式:
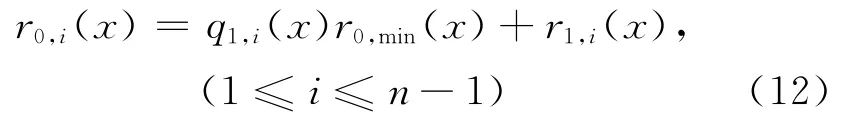
对rj,i(x)进行式(10)、(11)和(12)递归计算,结束条件为i=1、2,记此时j=m。定义rm,1(x)和rm,2(x)为 {c1(x),c2(x),…,cn(x)剩 余 项 多 项 式。其 中 qj,i(x)和 rj,i(x)分 别 为 rj-1,i(x)除 以rj-1,min(x)所得的商多项式和余数多项式。
3)对剩余项多项式rm,1(x)和rm,2(x)进行辗转相除,这里i≥1。即:
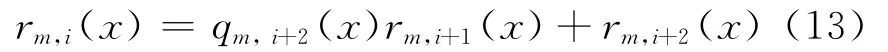
结束条件为deg(rm,i+2(x))≤L,设此时N =i+1并记录rm,N(x)=rm,i+1(x)。
4)设gk,-1(x)=0,gk,0(x)=1,(x)=1,(x)=0,rr-1(x)=ck(x),rr0(x)=rm,N(x),(1≤k≤n,下标r为标记)。对i≥1,定义qqi(x)和rri(x),满足:
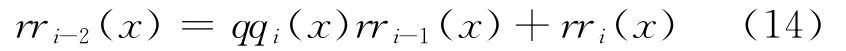
对gk,i(x)和(x)递归计算:
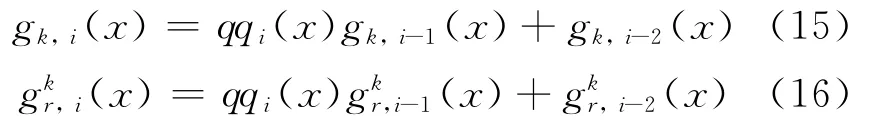
结束条件为deg(rri(x))≤L,设此时i=I,则gk(x)=gk,I(x)即为第k个码字对应的生成多项式,重复此步骤即可求出(n,1,m)卷积码的n个码字生成多项式:

需要说明的是,以上运算均是建立在F2(x)上。
3 实例仿真
以(3,1,6)和(5,1,9)卷积码为例验证该算法的可行性。
例1:(3,1,6)卷积码的生成多项式用八进制数表示为G (171,133,115),即
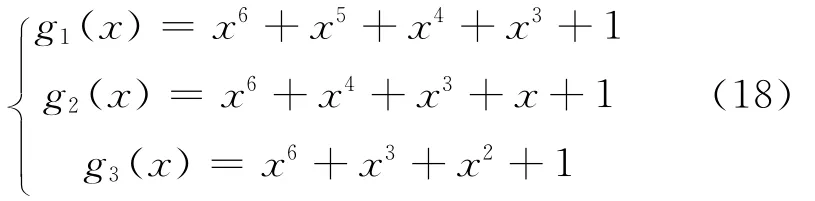
下面是接收到该卷积码的一段码字同步的编码序列:1 1 1 1 0 0 0 0 1 1 0 0 0 1 1 1 0 0 0 1 0 1 1 0 1 1 1 1 0 0 1 1 0 1 0 1 0 1 1 1 0 0 0 1 0 0 1 1 1 1 0 1 1 1 0 0 1 0 1 0 1 1 1 1 1 1 1 0 0 1 1 0 0 0 0 0 1 0 0 0 0 1 1 0 1 1 0 0 1 1。
按照2.3节所述的步骤对该序列进行识别,由该段编码序列得:
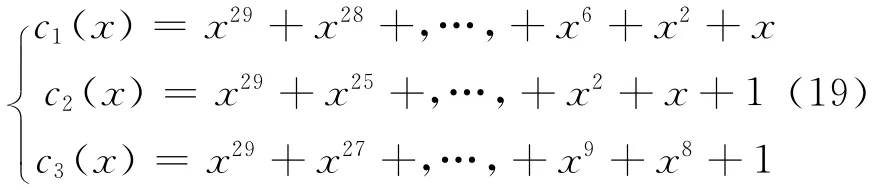
取r0,min(x)=c2(x),由步骤2)得表1。

表1 剩余项多项式的求解过程Tab.1 Process of solving the residual polynomial
对r1,1(x)和r1,2(x)进行步 骤 3)计 算,得r1,N(x)=r1,5(x):
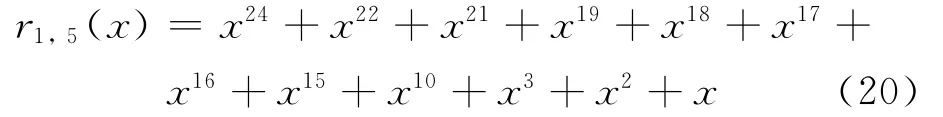
对r1,5(x)和c1(x),c2(x),c3(x)进行步骤4)计算,过程如表2所示,识别结果为:g1(x)=x6+x5+x4+x3+1;g2(x)=x6+x4+x3+x+1;g3(x)=x6+x3+x2+1,可见与式(18)相同,结果正确,验证了算法的可行性。

表2 gk(x)的识别过程Tab.2 Process of recognizing gk(x)
例2:同理(5,1,9)卷积码生成多项式为G (1635,1327,1517,1167,1333),即

接收到该卷积码的一段码字同步的编码序列为:1 1 1 1 1 0 1 0 1 1 1 0 0 1 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 0 1 0 0 1 1 1 1 0 1 1 1 0 1 1 0 0 1 1 0 0 0 0 1 0 0 0 1 0 0 1 1 0 0 1 1 0 0 1 0 0 1 1 1 0 1 1 1 1 1 0 0 0 1 1 0 0 0 0 1 0 0 1 1 1 0 0 0 1 0 1 0 0 1 0 0 1 1 1 0 0 1 1 1 0 0 1 0 1 0 1 1 1 1 0 0 0 0 0 0 0 1 0 0 1 1 1 0 0 0 1 0 1 1 0 1 1 1 0 1 1。由该序列得码字多项式:
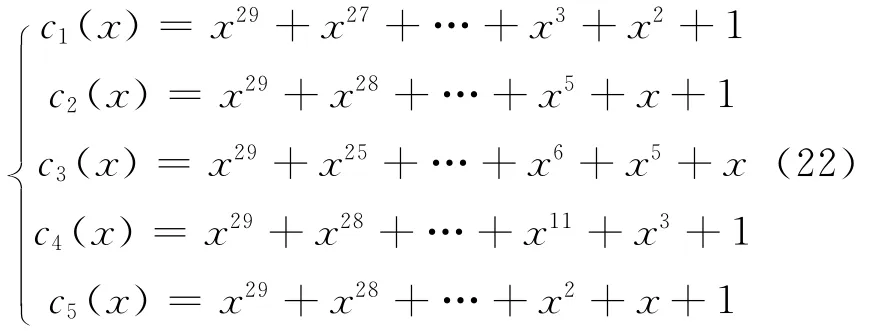
取r0,min(x)=c3(x),经计算剩余项多项式为r3,1(x)=x23+x20+…+x5+x3+x2和r3,2(x)=x24+x22+…+x2+x+1。对r3,1(x)和r3,2(x)进行步骤3)计算,得N即:
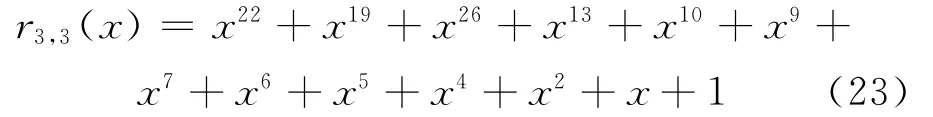
由步骤4)对生成多项式进行识别,结果为:g1(x)=x9+x8+x7+x4+x3+x2+1,(x)=x9+x8+x3+x2+1;g2(x)=x9+x7+x6+x4+x2+x+1,r(x)=x9+x5+x4+x3+x2+x+1;g3(x)=x9+x8+x6+x3+x2+x+1,r(x)=x9+x8+x7+x6+x5+x4+1;g4(x)=x9+x6+x5+x4+x2+x+1,(x)=x9+x7+x5+x+1;g5(x)=x9+x7+x6+x4+x3+x+1,(x)=x9+x5+x4+1。
可见gk(x)与式(21)相同,结果正确,验证了算法的可行性。
4 结论
本文提出了基于改进欧几里德算法的(n,1,m)卷积码识别方法。该方法利用求解n个多项式最高公因式的改进欧几里德算法解决(n,1,m)卷积码识别问题,只要求码字多项式最高幂次大于记忆长度m,即截获的码字序列长度大于其约束度,通常(n,1,m)卷积码的约束度n·(m+1)不大于96,所以能够利用较少数据(小于100bit)实现对所有(n,1,m)卷积码的准确识别,克服了文献[1]只能针对(2,1,m)卷积码识别的局限性,弥补了文献[3]所需数据量大和运算复杂的不足。
[1]WANG Fenghua,HUANG Zhitao.A method for blind recognition of convolution code based on euclidean algorithm[C]//IEEE Inter Conference on Wireless Com Networking and Mobile Computing.US:IEEE,2007:1 414-1 417.
[2]邹艳,陆佩忠.关键方程的新推广[J].计算机学报,2006,29(5):171-178.ZOU Yan,LU Peizhong.A new generalization of key equation[J].Chinese Journal of Computers,2006(5):171-178.
[3]薛国庆,常逢佳,柳卫平,等.1/n卷积码盲识别[J].无线通信技术,2009(3):38-42.XUE Guoqing,CHANG Fengjia,LIU Weiping,et al.Blind identification of 1/n convolutional codes[J].wireless communication Technology,2009(3):38-42.
[4]Andre Neubauer,Jurgen Freudenberger,Volker Kuhn.Coding theory algorithms,architectures and applications[M].北京:人民邮电出版社,2009.
[5]万哲先.代数导引[M].北京:科学出版社,2010.
