基于分组粒子群的飞行目标定位方法

姚金杰，韩 焱，王黎明，白培瑞

（1.中北大学电子测试技术国家重点实验室，山西 太原 030051；2.山东科技大学信息与电气工程学院，山东 青岛 266510）

0 引言

基于地面基站的目标定位技术已广泛应用于航空、航天、交通、物质勘探等领域，时差定位作为目标定位的一种方法［1］，已有chan、Taylor等求解算法［2］，但其推导复杂，且要求已知参数过多，不利于工程实现。

针对这一问题，粒子群优化算法（PSO）等群智能方法［3－4］也逐渐引入到目标定位领域。虽然PSO算法具有原理简单、参数少、收敛速度快、易于程序实现等特点［5－6］，但由于缺乏局部区域精细搜索能力，PSO算法在搜索后期会出现收敛停滞现象。目前，在基于种群多样性［7］的粒子群算法改进中，主要有变异粒子群算法（MPSO）［8－9］、吸引－排斥粒子群算法［10］（ARPSO）等，这些改进策略极大提高了粒子群全局寻优的能力，克服了PSO易陷入局部最优的缺点，但仍存在收敛速度慢、计算量大的不足。基于此，本文提出了飞行目标轨迹定位的分组粒子群优化算法。

1 基本原理

1.1 飞行目标定位原理

利用时差定位技术（TDOA）对空间飞行目标进行定位时，其原理是通过测量无线电信号到达不同基站天线单元的时间差，对发射无线电信号的目标进行定位，如图1所示。

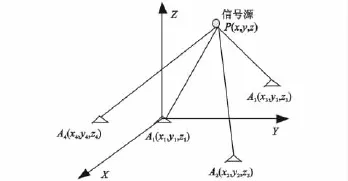
图1 目标定位示意图Fig.1 Chematic diagram of target localization

图1中，待测的目标空间位置为P（x，y，z），地面基站的空间位置为 Ai（xi，yi，zi），其中，i＝1，2，3，4。并设A1（x1，y1，z1）为主站位置，其他接收站为副站。则利用TDOA测量值进行飞行目标定位的模型为：

式（1）中，Ri表示信号源与第i站之间的距离，Ri，1表示信号源到第i站与其到主站之间的距离差，c表示无线电磁波的传播速度，取3×108m／s，τi，1是信号源信号到i站与其到主站之间的时间差。式（1）表明进行目标定位就是求解该方程组的解。

1.2 标准粒子群算法（PSO）

设在一个D维目标搜索空间中，由m个粒子组成一个种群，第i个粒子的位置用向量xi＝ ［xi1，xi2，…，xiD］表示，飞行速度用vi＝ ［vi1，vi2，…，viD］表示，最优位置为pi＝ ［pi1，pi2，…，piD］，整个粒子群搜索到的最优位置表示为pg＝ ［pg1，pg2，…，pgD］，粒子根据下式来更新其速度和位置：

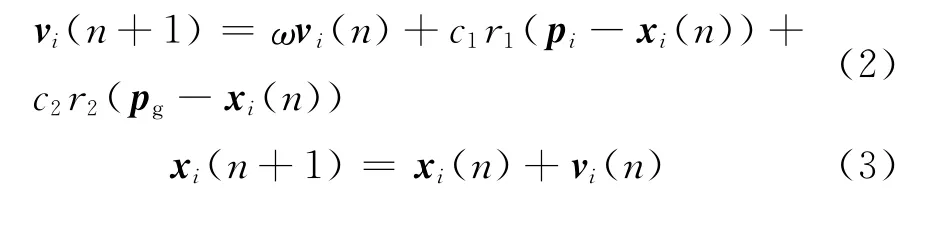
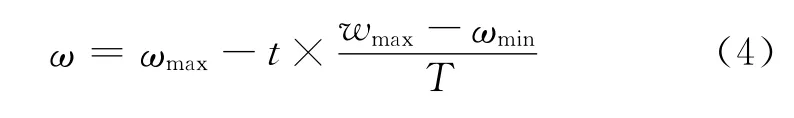
式（2）与式（3）中，i＝1，2，…，m，c1，c2是学习因子，为非负常数；r1，r2是均匀分布在（0，1）区间的随机数；ω为惯性权重，ωmax为最大惯性权重，ωmin为最小惯性权重，t为当前迭代次数，T为总的迭代次数。粒子在解空间内不断跟踪个体极值与全局极值进行搜索，直到达到规定的迭代次数或满足规定的误差标准为止。PSO算法的求解步骤如下：

步骤1：设置种群规模、迭代次数、学习因子等粒子群参数，确定目标变量；

步骤2：初始化种群各粒子位置和速度；

步骤3：计算种群适应度，并按适应度排序，将全局最优个体和当前最优个体分别进行存储；

步骤4：更新粒子的速度和位移；

步骤5：计算新粒子群的适应度，更新粒子全局极值和个体极值；

步骤6：判断算法是否满足收敛条件，如果满足，执行步骤7，否则转向步骤4；

步骤7：将全局最优个体输出，即完成目标位置解算，运行结束。

2 分组粒子群优化算法

标准粒子群算法在搜索后期存在陷入局部最优的风险是因为种群多样性的丧失而造成的。因此，通过反馈种群多样性信息控制进化的过程，可以保持种群多样性，降低算法陷入局部最优的风险。同时，在进化过程中，不单纯地整体进化，而是化整为零，充分发挥各粒子子群的能动性，使种群能够从各种途径达到全局最优。依据该思想，本文提出了分组粒子群优化算法（DGPSO）。

1）种群多样性反馈

种群多样性是整个种群搜索状态的参考，当多样性减小时，种群将处于局部搜索状态，有陷入局部最优的风险；当多样性增大时，种群将处于全局搜索状态，收敛速度将变慢。因此，种群多样性测度可表示为：

式（5）中，｜S｜表示种群规模，｜L｜表示搜索域的最长对角线长度，D表示目标维数，pi，j表示第i个粒子的第j维分量，表示所有粒子第j维分量的平均值。

2）分组粒子群优化算法

在标准粒子群算法的基础上，结合种群多样性控制的思想，当种群多样性小于某一阈值时，将种群等分量分为两个子群，其中一个子群进行排斥进化操作，即：

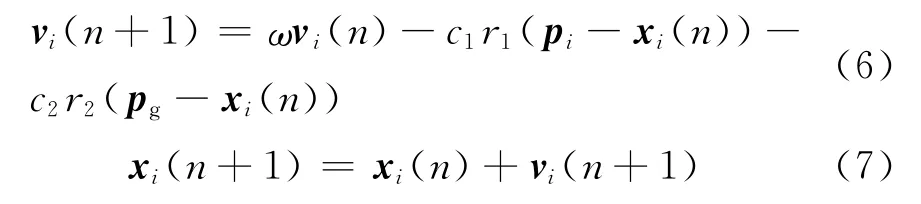
式（6）是式（2）的反状态，表示粒子按相反方向进化，排除相同性，使粒子多样性得到增加。

另一个子群引入高斯变异操作，使得粒子陷入局部聚集时能够朝新的方向重新搜索，增大寻找全局最优解的几率，即

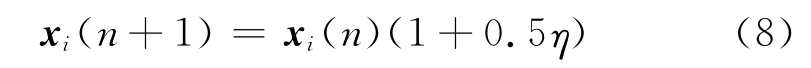
式（8）中，η是服从 Gauss （0，1）分布的随机变量。算法根据群体中粒子的位置状态自适应地调整变异操作，达到粒子过于集中时打散继续搜索的目的。

与PSO算法相比，利用分组粒子群优化算法对目标进行定位的算法步骤是在PSO算法步骤3和步骤4之间加入以下步骤：

1）评价种群多样性，如果小于设定阈值，执行2），否则执行PSO的步骤4；

2）将种群等分为两个子群；

3）子群进化，其中一个子群按照式（6）和式（7）进行排斥进化操作，另一个子群按照式（8）进行高斯变异操作。

3 仿真及分析

在目标定位仿真中，设基站数目为4，以平行四边形分布在三维空间中，其中主站坐标为（0，－5 000，0），辅 站 坐 标 为 （－10 000，100，10），（20 000，－100，5）和（30 000，5 000，20），目标理想运动轨迹为抛物线模型，如式（9）所示：

式（9）中，x0，y0，z0为起点坐标，vx，vy，vz分别为目标飞行速度在三维方向上的分量，g为重力加速度，发送信号间隔为500ms，时差测量方差为10ns。

分组粒子群优化算法（DGPSO）的参数选取如下：学习因子c1和c2为2，最大加权因子ωmax为0.9，最小加权因子ωmin为0.4，粒子群的种群大小为20，总的迭代次数为300，种群多样性阈值为5×10－6。根据目标定位原理，利用分组粒子群优化算法对获取的时差数据进行定位，如图2所示。

图2 基于分组粒子群优化算法的目标定位Fig.2 Target localization based on DGPSO algorithm

图2中，估计目标运动曲线与理想运动曲线基本一致，对其进行均方误差分析，结果如图3所示。

图3 目标定位的均方误差（RMSE）曲线Fig.3 RMSE of target localization

从图3中可以看出，在时差测量误差为10ns的条件下，分组粒子群优化算法（DGPSO）的定位均方误差RMSE在12m以内。为了进一步分析该算法与PSO、MPSO和ARPSO算法的差别，对其作平均适应度分析，如图4所示。由图4可知，DGPSO的收敛速度最快，MPSO算法的收敛速度最慢，而PSO和ARPSO的收敛速度基本一致。进一步从误差均值、误差方差、计算量方面进行比较分析，如表1所示。表1中，分组粒子群优化算法整体性能更好，更容易在短时间达到较高定位精度。

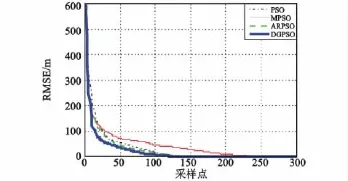
图4 平均适应度随迭代次数变化关系曲线Fig.4 Relationship between average fitness and iterations numbers

表1 目标定位求解算法指标比较Tab.1 Comparison among target localization methods

4 结论

本文提出了飞行目标轨迹定位的分组粒子群优化算法。该算法在标准粒子群算法的基础上，根据种群多样性选择合适的分组变异时机，分别进行排斥进化操作和高斯变异操作，实现快速有效的飞行目标运动轨迹测量。仿真结果表明：基于分组粒子群的飞行目标定位方法收敛速度快、定位精度高、计算量小，解决了飞行目标运动轨迹快速有效的测量问题。

［1］刘利军，韩焱.基于最小二乘法的牛顿迭代信源定位方法［J］.弹箭与制导学报，2006，26（3）：325－328.LIU Lijun，HAN Yan.Newton iterated signal source localization algorithm based on the least squares method［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2006，26（3）：325－328.

［2］Guoqiang Mao，Baris Fidan，Brian D O.Anderson.Wireless sensor network localization technique［J］.Computer Networks，2007（51）：252 9－255 3.

［3］史洪宇，燕莎，曹建忠.无线传感器网络节点定位的混沌粒子群优化算法［J］.探测与控制学报，2010，32（5）：46－49.SHI Hongyu，YAN Sha，CAO Jianzhong.Chaos particle swarm optimization algorithm for wireless sensor networks node localization［J］.Journal of Detection ＆ Control，2010，32（5）：46－49.

［4］姚金杰，韩焱.基于改进自适应粒子群算法的目标定位方法［J］.计算机科学，2010，37（10）：190－192.YAO Jinjie，HAN Yan.Research on target localization based on improved adaptive velocity particle swarm optimization algorithm［J］.Computer Science，2010，37（10）：190－192.

［5］王勇，张伟，陈军，等.改进粒子群优化算法研究［J］.计算机科学，2009，36（8）：258－259.WANG Yong，ZHANG Wei，CHEN Jun.Study of improved particle swarm optimization［J］.Computer Science，2009，36（8）：258－259.

［6］孙向军，赵斯强，严宗睿.基于粒子群优化的反潜搜索研究［J］.微电子学与计算机，2008，25（10）：91－93.SUN Xiangjun，ZHAO Siqiang，YAN Zongrui.Antisubmarine search research on the optimization of particle swarm［J］.Microelectronics ＆ Computer，2008，25（10）：91－93.

［7］焦巍，刘光.基于多样性反馈的粒子群算法［J］.计算机工程，2009，35（22）：202－204.JIAO Wei，LIU Guangbin？？？.Particle swarm optimization algorithm based on diversity feedback［J］.Computer Engineering，2009，35（22）：202－204.

［8］蔡昭权，黄翰.自适应变异综合学习粒子群优化算法［J］.计算机工程，2009，35（7）：170－171.CAI Zhaoquan，HUANG Han.Comprehensive learning particle swarm optimization algorithm with adaptive mutation［J］.Computer Engineering，2009，35（7）：170－171.

［9］Xing L N，Chen Y W，Yang K W.A novel mutation operator based on the immunity operation［J］.European Journal of Operational Research，2009，197：830－833.

［10］Riget J，Jakob S.Vesterstr.A diversity－guided particle swarm optimizer－the ARPSO［EB／OL］.［2012－03－12］.http：／／citeseer.nj.nec.com／riget02diversityguided.html.