RDS基带编码CRC算法的研究
2012-11-29于丽秋
于丽秋,路 勇
(北京交通大学 电子信息工程学院,北京 100044)
RDS(广播数据系统,Raidio data System)是一种应用在无线广播领域中的技术。在不增加传输信道的情况下,调频立体声广播可以增加多种通信业务,传送多工信息。由于在通信系统中可靠性与传输率往往是相互制约的,当要求提高传输率时,校验码位数就必须要少,这样在受到干扰后会产生错误的可能性增加,传送信息的可靠性下降[1]。当要求可靠性时,校验码位数就要增加,这就导致传送的速率变慢。为了降低信道内噪声及信道传输特性不理想造成的传输差错,在要求的传输率下,尽可能的提高通信的可靠性,在RDS系统中采用CRC(循环冗余效验码,Cyclic Redundancy Check)缩短码编码技术对可能或已经出现的差错进行控制[2]。
1 RDS基带信号编码格式
在RDS基带编码的结构中,以“组”为单元,每组包含4个块,每个块有26 bit,其中包含16 bit信息字和10 bit检验字,整个组共有104 bit[6]。
在该结构中信息字、校验字、二进制数或二进制地址都是先传送高位,数据传送是完全同步的,各数据块与数据组之间不留空隙。其中,为了使传送的信息误码校验和组块同步,校验字部分是由信息字生成的校验字模2加上组和块同步的偏置字。在这里主要研究由信息字生成的校验字的两种不同CRC并行算法,及仿真和综合结果的分析。
2 适用于RDS基带信号的误码校验
RDS数据格式使用了一种缩短循环的块编码,它是由原始长为341 bit的循环码315 bit而得到的(26,16)分组纠错码. 所用编码是一种最佳的纠正突发误码的缩短循环码,其生成多项式为[7]:
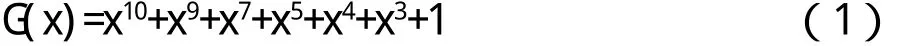
为了使接收机的解码器能检测出并纠正传送中的误码,故在发送端每发送一个26 bit块就含有10 bit校验字,这正是选择(1)式所示的生成多项式的原因。
下面介绍以信息字生成的校验字的形成方法。
(1)将16 bit信息字多项式左移10 bit;
(2)用(1)式得到的新的26 bit多项式除以生成多项式G(x),得到的余数多项式R(x);
(3)余数多项式R(x),即为所求的校验字。
CRC缩短循环码有明显的分组码结构,即前16 bit是信息位,后10 bit是检验位,这种结构利于在解码时快速提取信息位。对于信息位和校验位的编码过程,通常会考虑用它的生成短矩阵G,关于短阵G的详细说明及生成过程参考相关文献。

3 对常见的CRC算法实现的分析研究
CRC码常见的算法主要有串行和并行算法。
串行数据通信中有着得天独厚的优势,电路成本低,占用资源少;但是如果要求提高串行通信的速度就得完全依赖于时钟频率的提高,对于速度要求较高的场合,特别是实时通信,用串行通信就很难满足要求。
CRC码的并行计算方法对于高速的实时通信的要求非常高,对于长帧结构,采用并行算法有利于减少算法的运算时间,但其所占用的资源相对于串行算法要多,同时要有严格的数学算法模型。
下面将通过对两种不同的并行算法的仿真综合结果进行分析和对比,来找到适合RDS 传输的校验码算法。
3.1 异或并行算法
将根据短阵G给出RDS传输的检验码(26,16)的VHDL编码器的算法,该算法的信息字与校验字的逻辑关系如表1,它其实是利用短阵G的相应的信息位之间的异或运算来直接得到校验字的不同位。具体的VHDL代码就是根据表1得到的。
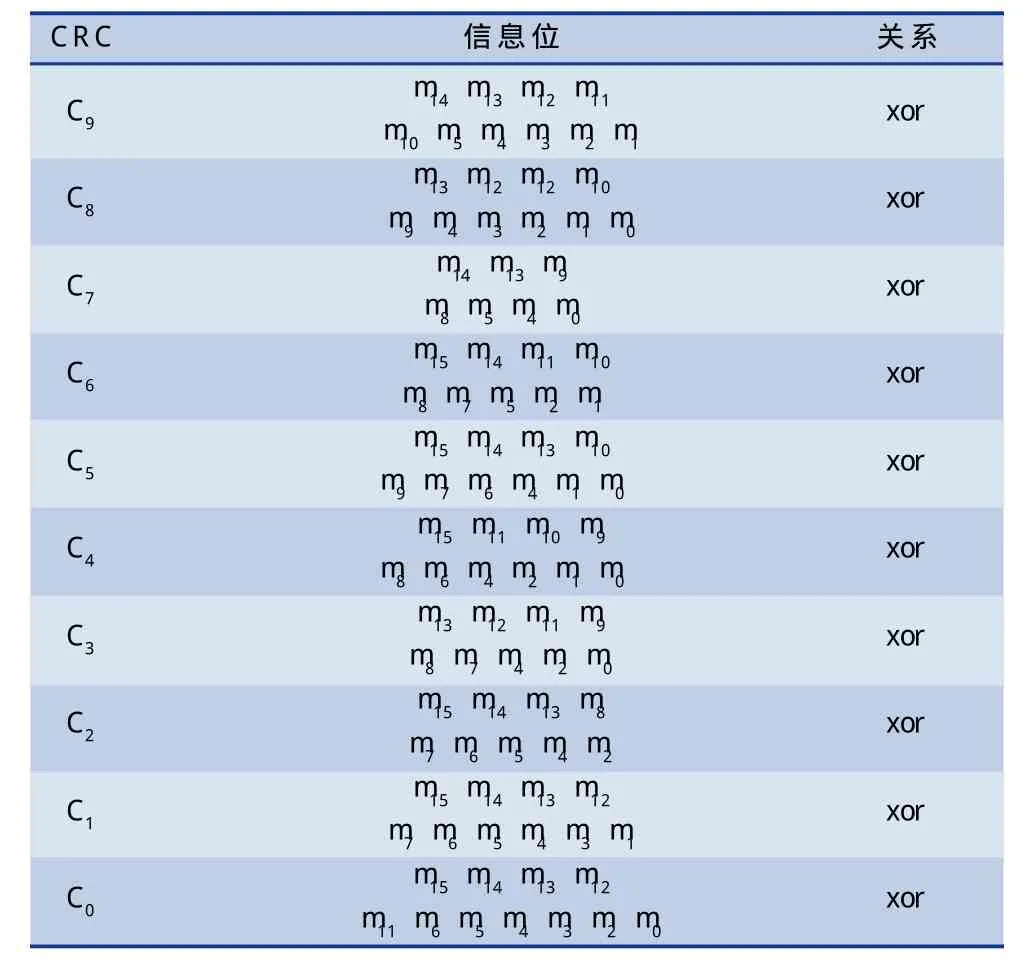
表1 校验位与信息位的逻辑关系
3.2 循环并行算法
下面给出的算法是模拟人脑思维的并行算法,它主要是利用VHDL的循环语句来实现的,其具体实现的流程图如图1 。
从流程图1中看出,该方法主要是根据实际中每次的模2除法后所得的余数来判断余数最高位是否为“0”,如果为“0”时,则从信息位依次后补位数,直到为“1”,接着进行模2除法,循环处理。直到最后所得到的余数,即为信息字的校验位。
4 仿真结果
根据上面给出的两种不同的并行算法,将通过对这两种并行算法的时序仿真波形、占用资源情况及延迟时间这3方面来进行分析比较,来找出来找到适合RDS传输的校验码算法。
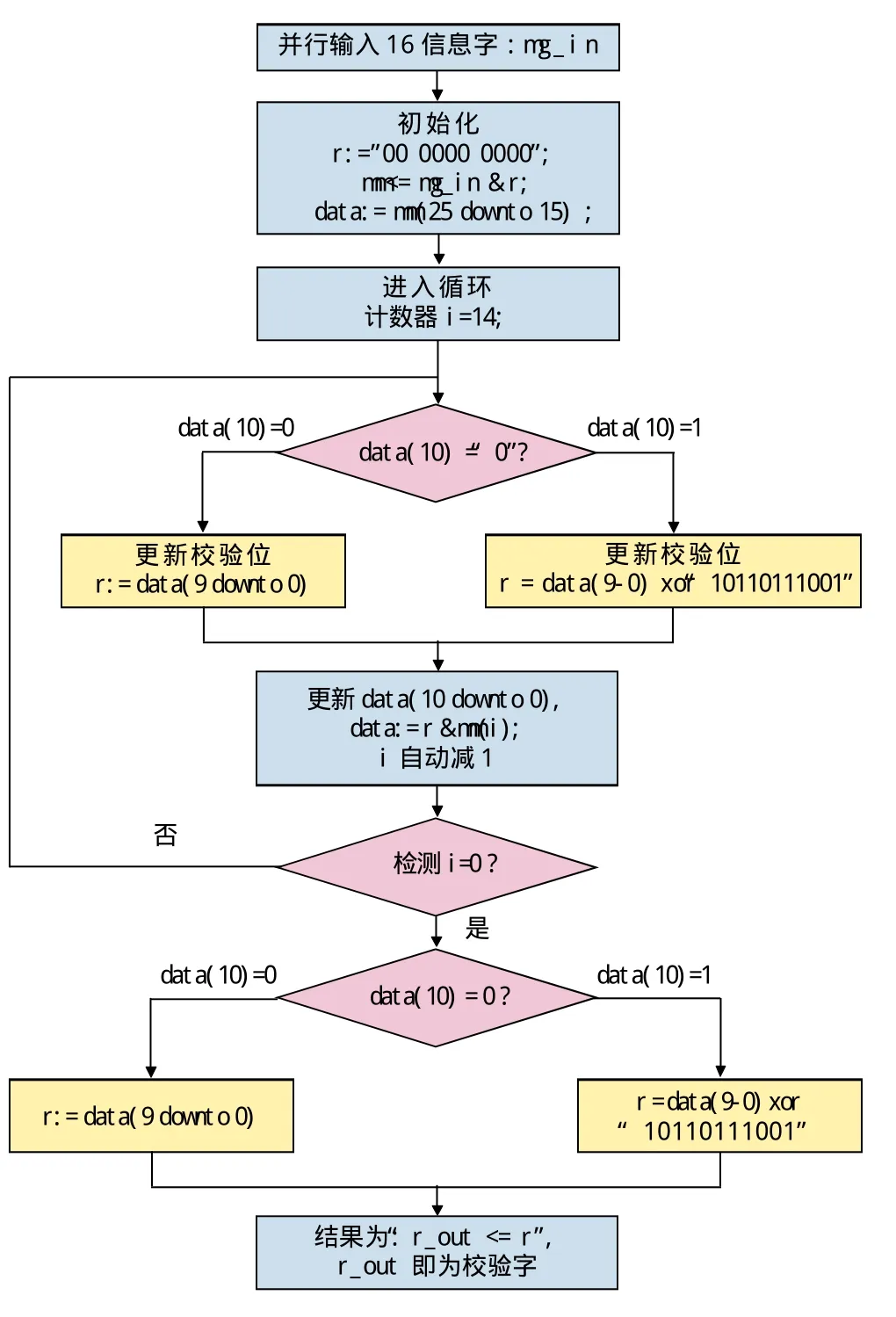
图1 循环并行算法流程图
4.1 功能仿真
本仿真采用的是Xilinx ISE 10.1软件平台自带的仿真工具进行功能仿真,采用的是Spartan系列的XC3S500E芯片进行功能仿真,由于异或并行算法和循环并行算法所实现算法功能相同,所以它们所形成的功能仿真波形图相同,如图2。

图2 功能仿真
4.2 资源占用情况
利用短阵G的逻辑关系进行的异或运算来实现的算法,其占用资源的情况如图3。
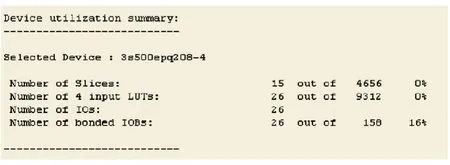
图3 异或运算资源占用情况
运用模拟人脑思维的模2并行循环算法,所占用的资源情况如下图4。
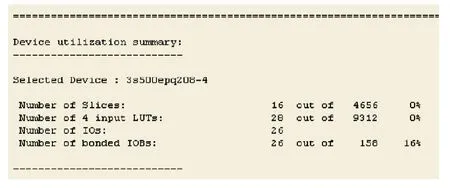
图4 循环运算资源占用情况
根据以上给出的这两种算法占用资源的情况来看,可以得出,Slices的占用情况为,异或并行算法使用量为15,循环并行算法则为16;
而异或并行算法占用LUT2、LUT3和LUT4的资源数量分别为8、3、和15;而循环并行算法使用LUT2、LUT3和LUT4的资源数量分别为1、8和19,故异或算法比循环算法占用LUT资源相对节省约0.21%。
4.3 延时时间情况
下面将给出这两种算法的延时时间的情况,并对它们的延时时间进行分析和对比。
(1)异或并行算法的时间延时情况的报告结果如图5 。

图5 异或运算时间延迟情况
(2)循环并行算法的时间延时情况的报告结果如图6 。
从以上这两种并行算法的时间延时情况,可以看出,异或算法总的延时的时间为8.051 ns,而循环算法总的延时时间为14.242 ns,由于延迟时间短,信息传输速率就快,所以可以得出异或并行算法的传输时间相对于循环并行算法的传输时间要快6.191 ns,尤其在进行大量的数据信息传输时这种优势就会更加明显。
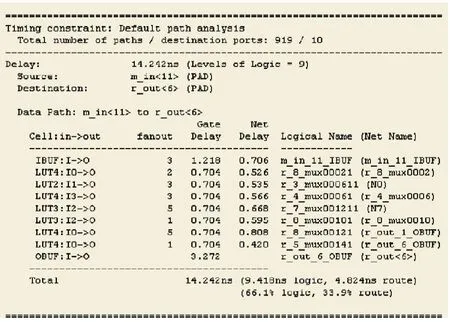
图6 循环运算时间延迟情况
5 结束语
通过上面对这两个不同的并行算法的仿真时序,占用资源及延时时间的结果分析和对比,很容易看出,无论从占用资源情况还是延时时间上,异或并行算法都要比循环并行算法占优势,尤其是对于传送多位的数据信息字的通信系统来说就优势就更突出了,可以得出,异或并行算法要比循环并行算法更适合RDS传输的校验码算法。
[1]唐 跃. 编码在通信中的应用[J]. 湖北广播电视大学学报,2006(5).
[2]顾文斌,王 怡,马 莉. 基于FPGA的CRC算法的实现[J]. 计算机与现代化,2008(5).
[3]叶 懋,刘宇红,刘 桥. CRC码的FPGA实现[J]. 重庆学院学报(自然科学版). 2007, 21 (3):85-87.
[4]梁少洁,常天海. 循环冗余校验码并行算法的FPGA实现[J]. 广东通信技术,2008(2):57-59,63.
[5]王海光. 并行CRC算法硬件实现研究与VHDL设计[J]. 漳州师范学院学报(自然科学版),2007(4):51-56.
[6]卢云川,过 静. RDS编码和解码技术及应用[J]. 工程勘察,2000(2):50-52,58.
[7]姚冬苹,蔡超时,宋宜纯. 广播数据系统(RDS)的信道编解码[J]. 铁道学报,1997(2):46,71-75.
