基于非线性数学模型的麻疯树树体构型优化设计

蔡小虎，张启珍，陈翰林

(1.四川省林业科学研究院，四川成都 610081;2.理县林业局，四川理县 623100;3.西南科技大学理学院，四川绵阳 621010)

生物柴油以可再生的动植物油为原料并且对环境清洁等优势，在国际国内已引起广泛的关注。发展生物能源，高效利用生物质能源，是我国石油安全战略的重要组成部分，也是解决我国“农林业、能源、环境”难题的最佳切合点和实现能源、经济和生态效益的良性循环共同发展的重要战略途径之一［1］。

麻疯树产油高，生长条件要求低，非常易存活，可在荒地种植［2，3］，具有“不与农争地，不与民争粮”等优点，正在逐渐成为生产柴油的重要原材料［4～7］。然而，实现麻疯树高、稳产及规模化培育，是目前尚未解决的难题［8，9］，而研究树体构型［2］进而找出一种最优化的树体结构，对解决这一难题将起到关键作用。

1 疯树生长特征及其树体构型

影响麻疯树的树体结构的因素很多［11～14］，而树体结构又与枝条分布有密切关系，在很大程度上影响着果实产量的提高。通过实地观察四川攀西地区自然状态下生长的以及人工栽培的麻疯树，得出麻疯树具有以下生长特征:

(1)麻疯树的茎为合轴分枝，整个麻疯树植株成为开心形的圆锥状株冠。

(2)具有多级分枝性:从主茎上长出一级分枝，一级分枝上长出二级分枝，以后则相继生长出三级和四级分枝等。

(3)麻疯树在枝条上下级的节点处结果。

(4)分枝角度特别是树体下部一、二级分枝部分对麻疯树枝条向空间扩展的能力起着重要的决策作用。

(5)麻疯树一、二级枝条分枝较多，三级以上等则明显减少。

(6)麻疯树整株树高一般在3 m～4 m范围，就人工栽培的而言，其冠幅一般不超过人为控制的间距。

根据以上基本特征，我们得出以下结论:

(1)若只考虑影响麻疯树果实产量的树体本身因素，则在一定的空间内，枝条数量越多则挂果越多。

(2)分枝角度可作为衡量麻疯树枝条空间分布能力大小的一个重要指标，在一定范围内，若枝角越大则枝条的空间扩展能量将越大，反之则不然。

(3)麻疯树一、二级枝条是整个树体的支撑部分

(4)若在一定空间范围内来研究麻疯树的树体构型，可将冠幅和树高作为横、纵向研究枝长的约束性条件。

基于以上对麻疯树树体特征，通过构型模型分析［15～17］，建立麻疯树生长最优树体构型模型。

2 麻疯树树体构型模型分析

2.1 麻疯树分枝角度

分枝角度是麻疯树树体构型中一个重要的影响因子，在一定程度上可直接反应麻疯树树体结构优劣，所以对分枝角度的考虑是提出最优化树体构型不可或缺的部分。

2.1.1 一、二级枝条分枝角

观察成年麻疯树生长长势，将树体形态与一、二级分枝角度对应起来，可大致分为如下3种情况(图1)。

图1 不同一、二级分枝角对麻疯树生长空间影响的截面示意图Fig.1 Section schematic of spatial growth influenced by different branching angles of class 1 and 2 branches

在一定范围内，若分枝角度过小，树体构型呈图1a所示:树型较高，但冠幅较小，不能充分利用横向空间。若分枝角度过大，树型呈图1b所示:冠幅较大，但树不够高，不能充分利用纵向空间。

显然，在有限的生长空间内，对于人工栽培的麻疯树，合理的人为控制一、二级枝条的分支角度，使树体生长空间相对增大将在很大程度上增加麻疯树总生枝数，从而间接的提高麻疯树果实产量。

2.1.2 三级及以上枝条分枝角

从林业人员方便管理栽培的麻疯树的角度出发，考虑三级及以上的分枝枝条可假设为自然生长。一方面是由于一、二级枝条的生长状况已经能基本确定麻疯树树体构型的大致分布，三级及以上枝条的自然生长基本能达到预期期望制;另一方面，随着枝条密度以及树高的不断增加，人为控制的难度必然加大，若仍实施人为管理则将相应增加麻疯树栽培成本。

2.1.3 分枝角度建模

记符号αii(1≤i≤T，0≤ij≤Ni)为第i级第ij个枝条分枝角，则αij是待确定的目标量。由以上分析，当i≥3时，分枝角度同自然条件下生长。

本文采用的数据均是在麻疯树自然生长状态下测得的，对“树干分枝角度”数据进行统计分析，将结果应用于三级及以上的枝条在自然状态下的分枝角度研究。利用SPSS软件统计分析表明分枝角度α 服从正态分布 α ～ N(20.3091°，7.1099°)，对给定的概率为95%的置信区间为［18.3870，22.2312］。

2.2 麻疯树分枝数

在麻疯树幼苗生长初期，因为生长所需的营养以及空间等富裕充足，使得在前两个生长周期中分枝数较多，而以后生长周期中，由于空间枝条密度增大等原因，再分枝将明显减少。因此，从以下两个方面考虑麻疯树生长过程中的分枝情况。

2.2.1 第一、二周期分枝

在第一个生长周期中，用SPSS软件对实际数据进行正态检验与分析，分枝数N1服从正态分布N1～ N(5.4757，3.1261)。

在第二个生长周期中，每个一级枝条再分为二级枝条，记 N1，i1为第一级枝条中的第 i1个，n1，i1为第i1个枝条在下一周期即第二周期中产生的二级枝条数。

对一级枝条再分成的二级枝条数用SPSS分析，服从Weibull分布。在显著性水平α=0.05下，麻疯树一级枝条再分为二级枝条的数量服从Weibull分布时参数的点估计分别为［0.1300，1.6836］，n1，i1～W(0.1300，1.6836)。

2.2.2 第三周期及其以后的情况分析

考虑麻疯树在第三周期及其以后的生长周期中，按自然生长，分枝均匀。根据大量对麻疯树三级以上分枝数统计分析，这段时期每个枝头在下一周期中再生的的分枝数一般不超过3条，可令这段时间可取再分枝头数集合为 A={0，1，2，3}。

设麻疯树生长周期为T，第k个周期中产生的分枝数为Nk，Nk-1，ik-1表示第k-1个周期中第ik-1个枝条，nk-1，ik-1表示第ik-1个枝条在下一周期k中再生的枝条数。

则第i级的枝条数目为:

则经过T次生长周期后，麻疯树总枝头数为:

2.3 麻疯树枝长及父子级枝条缩放比例

在实际麻疯树种植中，每株麻疯树幼苗间横、纵向都有一定的距离，若在一定空间范围内来研究麻疯树的树体构型，可将冠幅和树高作为横、纵向方面研究枝长的约束性条件。

2.3.1 枝长约束性建模

基于麻疯树“在给定空间范围内生长”这一实验前提，成年麻疯树冠幅截面近视为椭圆，L设为椭圆的长半轴长，H表示成年麻疯树树高，h表示枝下高。

则麻疯树第T级枝条有如下表1中的关系:

表1 麻疯树第k级枝条枝长在横、纵向投影情况Table 1 Horizontal and vertical projection of branch length of Class k in Jatropha curcas L.

根据植物生长常识，分级越多，各级枝条在横、纵向投影最大值累积总和越大，所以将上表中横向约束与纵向约束归可纳为以下，有:

其中L，H为人工栽培时麻疯树半行间距及为方便果实采摘设定的最大期望树高，为实际设定的值，单位均为m。

在显著性水平αlpha=0.05下，麻疯树枝下高h服从 Weibull分布其时参数的点估计分别为:［0.0101，1.4117］，h ～W(0.0101，1.4117)。

2.3.2 父子级枝条缩放比例与分枝比例

自然状态下，树自根节点向端节点生长时，其长度将不断递减，从而导致每次分枝时父枝与子枝具有一定的缩放比例φ∈［0.8，1.0］。同时由于枝条密度不断增大，也会导致父子级枝条缩放，为此设分枝比例为ψ，

则

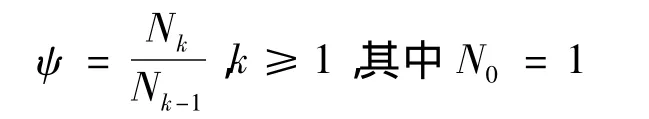
由此得到第k级枝条长度为:

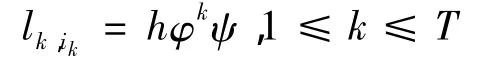
3 麻疯树树体构型的优化模型及求解

3.1 最优化树体构型模型

在一定生长空间范围内，建立以麻疯树枝条总数最多从而间接反映果实产量最高的目标函数，直接考虑一、二级枝条分枝角度、分枝数、枝条长度，间接考虑树高、枝下高、冠幅以及枝条分级。根据以上分析，得到如下麻疯树树体构型最优化模型。

3.2 最优化树体构型模型求解

根据模型3.1，设计算法编程利用MATLAB求解，令一、二级分枝角度范围为15°≤α≤70°(此范围能包括自然状态下的分枝角度的全部情况)，每个角度模拟150株麻疯树的生长情况。

当麻疯树生长至按照人工栽培时设定行间距为2L=3(m)和为方便果实采摘而设定期望树高为H=3(m)的条件时，得下图2的结果。

由图2，明显反映出当一、二级角度过小和过大时，横向空间和纵向空间分别不能被充分利用，而当角度分布于35°附近时，分枝总数、横向及纵向空间利用率同时为最大，由此确定麻疯树的一、二级枝条最佳分枝角度为35°。

在确定麻疯树的一、二级枝条最佳分枝角度为35°后，为进一步精确研究人工栽培下的麻疯树在2L×2L×H(cm3)的空间范围内的最终分枝次数、分枝总数及横纵向空间利用率，利用上述麻疯树最优化树体构型模型结果，模拟人工栽培及自然状态下的100株麻疯树生长，得到图3和图4。

图2 不同一、二级分枝角度下的达到生长空间限定时的平均分枝次数(次)、平均分枝总数(个)、平均横向空间利用长度(cm)与纵向空间利用高度(cm)关系图Fig.2 Average branch series，total branch number，horizontal spatial utilization length and vertical spatial utilization height while different branching angles of Class 1 and 2 arrive at the spatial limitation

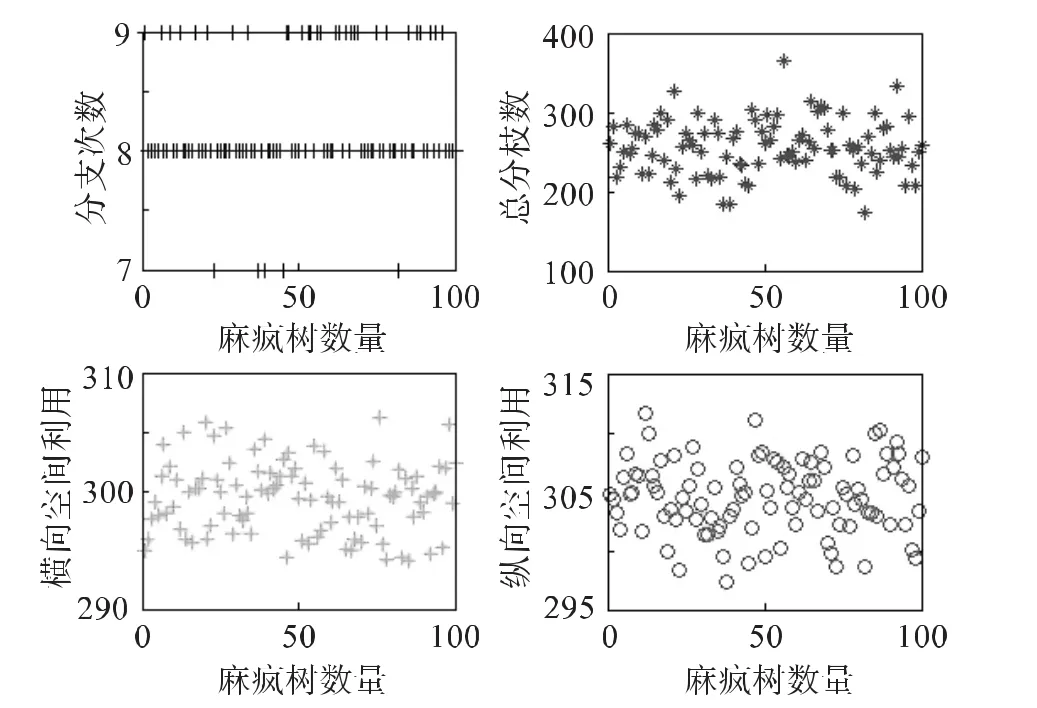
图3 优化模型下Fig.3 Optimized model

图4 自然状态下Fig.4 Normal model

对上述相关模拟结果统计、对比，得麻疯树生长关键指标的平均数值(表2)。

表2 自然状态与优化模型下模拟100株麻疯树各指标平均值Table 2 Average index values of 100 respective seedlings in normal and optimized models

由表2及图3、图4得出如下结论:因麻疯树每年抽梢2次～3次，当麻疯树平均分级次数达8次以后，每株麻疯树总分枝数量平均可达256个，横向及纵向空间均充分得到利用，经过2 a至3 a，麻疯树即可郁闭成林。

同时，相比在自然生长状态下，分枝次数、分枝总数、横向空间利用程度分别增加5.51%、18.09%及42.10%，纵向空间增长比例为-2.29%说明能更好的控制树高生长。

4 小结

对于分枝角度:麻疯树在进行第一及第二次分枝时，为保证成年麻疯树在一定的空间范围内拥有足够的枝条生长空间，分枝角度不可能精确控制到35°，所以可以通过切干或修剪的方式使一二级枝条的分枝角度约在30°～40°度左右即可，三级以上的枝条则自然生长，服从正态分布 N(20.309 1°，7.109 9°)，无需加以人工控制。

对于枝条数:一级枝条保留5～6枝，每只一级枝条再生的二级枝条数保留2枝～3枝，多余的枝条可通过人工修剪的方式予以剔除，三级以上枝条修剪情况可视麻疯树生长情况而定。

对于期望树高:根据以上模型分析出，可对麻疯树生长适当加以人工控制，使其生长高度在3 m左右，以方便果实采摘。

［1］钱能志，费世民，等.中国林业生物柴油［M］.北京:中国林业出版社，2008.

［2］Foidl N，Foidl G，Sanchez M，et al.Jatropha curcas L.as a source for the production of biofuel in Nicaragua.Bioresource Technology，1996，58:77 ～82.

［3］罗建勋，奉正顺，唐平，等.四川小桐子分布特点及适生环境选择初探［J］，西南林学院学报，2007，27(3):6 ～10.

［4］费世民，陈秀明，何亚，平.四川麻疯树生物柴油研究展望［J］.生物质化学工程，2006，40:193 ～199.

［5］Hanny Johanes Berchmans，Shizuko Hirata.Biodiesel production from crude Jatropha curcas L.seed oil with a high content of free fatty acids.Bioresource Technology，2008，99:1716 ～1721.

［6］Erwin C.Escobar，Rex B.Demafelis，Laura J.Pham，et al.Biodiesel production from Jatropha curcas L.oil by transesterification with hexane as cosolvent.Philippine Journal of Crop Science(PJCS)December，2008，33(3):1 ～13.

［7］Shikha Roy.Biofuel production frim Jatropha curcas.Biomass for energy and industry，2009，613 ～615.

［8］A.Nagaraju，S.Karimulla，Accumulation of elements in plants and soils in and around Nellore mica belt，Andhra Pradesh，India-a biogeochemical study.Environmental Geology，2002，41:852 ～860.

［9］N.Sunil，K.S.Varaprasad，N.Sivaraj et al.Assessing Jatropha curcas L.germplasm in-situ—A case study.Biomass and bioenergy，2008，32:198 ～202.

［10］陈波，宋永昌，达良俊.木本植物的构型及其在植物生态学研究的进展［J］.生态学杂志，2002，21(3):52 ～56.

［11］何亚平，费世民，蔡小虎等.麻疯树构件的生殖配置研究［J］.四川林业科技，2009，30(3):1 ～7.

［12］何亚平，费世民，蔡小虎等.攀枝花市麻疯树生殖构件特征与雌雄花配置研究［J］.四川林业科技，2009，30(1):8 ～17.

［13］何亚平，王乐辉，费世民等.麻疯树2年生人工林构筑型对修枝与土壤肥沃性的响应［J］.四川林业科技，2010，31(5):21～29.

［14］刘朔，何朝均，何绍彬.不同施肥处理对麻疯树幼林生长的影响［J］.四川林业科技，2009，30(4):53 ～56.

［15］陈兰荪，宋新宇，陆征一.数学生态学模型与研究方法［M］.四川科学技术出版社，2003.

［16］陆征一，周义仓.数学生物学［M］，科学出版社，2006.

［17］王定江，非线性森林发展系统研究进展［J］.生物数学学报，2008，23(1):125 ～131.