大跨度中承式钢箱混凝土系杆拱桥稳定性研究

2012-11-27王明明

铁道标准设计 2012年11期

王明明

(铁道第三勘察设计院集团有限公司，天津 300142)

近年来，随着桥梁结构在设计、施工工艺等方面的飞速发展，很多造型新颖、结构受力复杂的大跨度系杆拱桥也同时得到很大发展。而以受压为主的大跨度系杆拱桥结构来说，其稳定问题和其极限承载能力问题是紧密联系在一起的，因此，拱桥稳定性与其强度问题有着同样的重要性。由于大跨度拱桥结构日益广泛地采用高强材料以及结构杆件的薄壁化，更显示出了拱桥稳定问题的重要性［1，2］。

本文结合一大跨度中承式系杆拱桥。该系杆拱桥主跨为108.0 m，两边的边跨为32.1 m。主跨拱肋矢高为25.0 m，矢跨比为1/4.32，边拱肋矢高11.75 m，矢跨比为1/5.19。两片拱肋中心线之间的横向距离为12.0 m。该系杆拱桥采用中承式钢箱混凝土结构，拱肋采用钢箱填充混凝土截面，桥面系布置为纵横梁体系+混凝土桥面板结构，设计上采用拱式连续梁体系，系杆拱主拱肋和主纵梁采用固结处理，为中承式系杆拱桥另一新型结构形式。鉴于该系杆拱桥在结构和受力上的独特性，对其稳定性进行研究是非常有意义的。

1 拱桥的稳定分析理论

从拱桥失稳的特点来讲，可以将拱桥的失稳问题分为第一类失稳问题和第二类失稳问题2种情况［3，4］。

1.1 拱桥第一类稳定分析理论

拱桥第一类稳定问题属于平衡分支问题，其本质是数学上的特征值问题，求解出的最小特征值就是拱桥的失稳临界荷载系数［1，2］。拱桥第一类稳定的线性求解方程为

式中［KD］——结构弹性刚度矩阵;

［Kσ］——结构初始应力刚度矩阵;

λ——拱桥荷载稳定系数;

{δ}——结构的位移增量。

第一类稳定的广义特征值方程如式(2)所示

由上述方程计算出的特征值，只有其最小值才有实际意义，其值对应的就是拱桥失稳的临界荷载系数。

1.2 拱桥第二类稳定分析理论

拱桥第二类稳定理论分析是采用平衡迭代的方法进行的。其非线性平衡方程［3，4］为

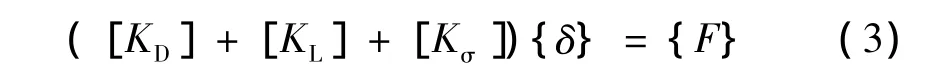
式中［KD］——结构弹性刚度矩阵;

［KL］——结构大位移刚度矩阵;

［Kσ］——结构初始应力刚度矩阵;

{δ}——结构节点处位移值;

{F}—结构等效节点处荷载值。

拱桥的压溃荷载即是考虑拱桥几何材料双重非线性所得的极限失稳荷载。

2 空间有限元分析模型介绍

利用ANSYS通用有限元计算分析软件，建立了三维全桥空间有限元分析模型。模型中采用空间梁单元、板壳单元以及空间杆单元对该系杆拱桥的各结构杆件进行模拟，全桥空间模型如图1所示。

2.1 单元选取

拱肋钢箱和拱肋混凝土截面:采用“双单元”法模拟拱肋钢箱和填充混凝土的相互作用，模型中选用beam188梁单元，此空间梁单元可以满足非线性收敛计算的需要。

图1 有限元模型立面

主纵梁:模型中采用beam4梁单元进行模拟。

混凝土桥面板:模型中采用plan163板壳单元进行模拟。

吊杆和预应力系杆:模型中采用link10杆单元进行模拟，并在计算时考虑吊杆和预应力系杆中的初始拉力荷载。

2.2 边界条件

计算模型中没有模拟桩基础与地基土之间的相互作用，建模时直接在拱座处按一般支承进行约束处理。在计算时主拱肋钢箱和主纵梁钢箱固结处采用共节点处理，边拱肋和主纵梁固结处通过设置刚臂进行连接。

2.3 荷载工况

利用上述建立的有限元计算模型，对该桥进行稳定性分析，本文只计算了成桥状态下的稳定性。模型中主要考虑以下4种荷载工况的组合。

恒荷载:系杆拱桥结构全部的自身重力。一期恒载:为拱肋和主纵梁等主体结构构件的重力;二期恒载:成桥后施加在主体结构上的轨道、栏杆等附属构造设施的重力。

列车活载:列车活载布置在桥梁主跨的范围内，按最不利位置进行加载。按照结构的受力特点，考虑双侧列车荷载。

人行道荷载:根据相关设计规范和本桥的设计文件，采用5.0 kN/m2进行计算。

横向风荷载:在计算模型中考虑拱肋钢箱、主纵梁钢箱、竖撑和吊杆的横向静风荷载作用，不考虑风荷载的动力作用。其计算按照《铁路桥涵设计基本规范》(TB10002.1—2005)中的有关公式进行计算。

2.4 拱桥有限元计算

到目前为止，大跨度拱桥结构的整体稳定性分析基本上是以线弹性理论为主，大跨度钢箱混凝土肋式拱桥，由于此种类型桥梁宽跨比较小，横向刚度相对较弱，大多是整体侧向外倾失稳，失稳时拱桥材料基本上已经进入弹塑性状态。此时，采用第一类稳定理论计算的临界荷载会偏于不安全，对结构产生安全隐患。因此，要准确计算拱桥的临界荷载，就要同时考虑拱桥几何材料双重非线性的影响。这样计算出的拱桥稳定性才更符合实际工程的失稳状况。

3 计算结果与分析

3.1 系杆拱第一类稳定计算分析

将系杆拱桥的稳定安全系数［5，6］定义如下

式中，Pt为桥梁结构施加的基本荷载;Pcr为结构失稳时对应的极限荷载值;稳定安全系数Kcr就是结构失稳状态时基本荷载Pt的加载倍数，反应桥梁结构对某种荷载工况的安全储备。

按照上述定义的稳定性安全系数，计算了拱桥的第一类稳定性，第一类稳定安全系数的计算结果如表1所示。

表1 各荷载工况下系杆拱桥第一类稳定安全系数

系杆拱桥的一阶失稳模态［7］如图2所示。计算结果表明:系杆拱桥在上述各荷载工况下的一阶失稳模态均为拱肋横向反对称失稳。

图2 系杆拱桥第一阶失稳模态

从表1可以看出:系杆拱桥的第一类稳定安全系数在荷载工况1作用下为44.265，在荷载工况2的作用下为36.360，对于成桥运营阶段其稳定安全系数是完全满足规范要求的。对于在荷载工况3的基础上加上横向风荷载的荷载工况4作用下，其稳定安全系数基本不变。由此可见，横向风荷载对系杆拱桥的第一类整体稳定性影响很小。而对比工况1和工况2可以看出，第一类稳定安全系数在加上列车竖向静活载后有显著的下降趋势，稳定安全系数降低达到17.9%。

3.2 系杆拱第二类稳定计算分析

3.2.1 系杆拱几何非线性稳定分析

在计算时，模型中只考虑桥梁结构自身恒荷载的作用。采用拱桥第二类稳定分析理论对该系杆拱桥的稳定性进行几何非线性分析［8］，图3即为主拱肋1/4截面处横向位移的P－Δ曲线。其中:Δ为主拱肋1/4截面处横向位移，K为计算模型中施加的荷载与基本荷载(恒载)Pt的比值，P－Δ曲线所计算K的最大值即为该系杆拱桥的稳定安全系数。

图3 主拱肋1/4截面横向位移的P－Δ曲线

从P－Δ曲线中可以看出:由于没有考虑拱桥的初始缺陷的影响，在荷载加载之初，结构并没有出现横向位移，随着荷载的增大，当所施加的荷载接近拱桥的极限失稳荷载时，此时其横向位移突然变大，P－Δ曲线基本上呈水平状态，说明该系杆拱桥此时已经不能满足正常的使用功能，结构已经失稳。

结合第一类稳定分析的计算结果还可以看出:该系杆拱桥第一类稳定安全系数为44.27，计入几何非线性因素影响后的稳定安全系数为43.82，后者比前者降低了1%。由此可以看出，对于本桥来说，考虑几何非线性影响对该系杆拱桥的稳定安全系数影响很小，计算时可以直接采用第一类稳定分析的结果。

3.2.2 系杆拱材料非线性稳定分析

在计算分析模型中，考虑了拱肋钢箱、主纵梁和桥面系钢材的材料非线性，同时考虑了拱肋填充混凝土和混凝土桥面板的材料非线性。计算时钢材和混凝土2种材料都按理想弹塑性材料考虑，钢材和拱肋混凝土的应力-应变本构关系［9］定义如下。

(1)钢材的应力-应变本构关系

Q370qD钢材的屈服应力为370 MPa。钢材的应力-应变本构关系曲线如下式表示。

式中，σy和εy分别为钢材屈服时的应力和应变值。

(2)混凝土的应力-应变本构关系

考虑到拱肋钢箱对拱肋填充混凝土的套箍作用将提高混凝土延性，拱肋内混凝土的应力－应变关系采用带有下降段的抛物线数学模型进行模拟［4，5］，其具体表达式如下所示

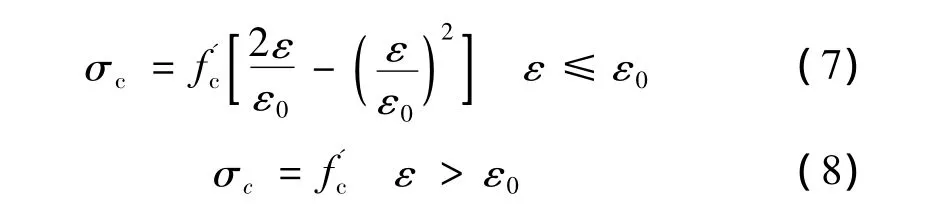
在计算时，模型中同样只考虑桥梁结构自身恒荷载的作用。利用上述定义的钢材和拱肋钢箱混凝土本构关系曲线，采用拱桥第二类稳定理论对该拱桥的稳定性进行材料非线性分析，图4即为主拱肋拱顶截面处竖向位移的P－Δ曲线。其中:Δ为主拱肋拱顶截面处的竖向位移，K为计算模型中施加的荷载与基本荷载(恒载)Pt的比值，P－Δ曲线所计算K的最大值即为该系杆拱桥的稳定安全系数。

图4 主拱肋拱顶截面竖向位移的P－Δ曲线

从P－Δ曲线中可以看出:在初始计算加载时，P－Δ曲线基本上呈线性变化趋势，当所施加的荷载值达到该桥的极限失稳荷载时，材料进入塑性状态，此时拱肋的位移迅速增大，拱顶处的P－Δ曲线基本上呈水平状态，结构出现失稳。计算结果表明:计入材料非线性因素影响时的稳定安全系数为11.16，而系杆拱桥的第一类稳定安全系数为44.27，其材料非线性稳定安全系数只有第一类稳定安全系数的1/4左右。由此可以看出，材料非线性对结构稳定安全系数影响很大，在计算该系杆拱桥的稳定安全系数时，材料非线性的影响一定不可忽略。

3.2.3 系杆拱双重非线性稳定分析

在计算时，模型中同样只考虑桥梁结构自身恒荷载的作用。利用上述计算模型，考虑几何和材料非线性同时计入计算模型中［10，11］，图5即为主拱肋拱顶截面处竖向位移的P－Δ曲线。其中:Δ为主拱肋拱顶截面处竖向位移，K为计算模型中施加的荷载与基本荷载(恒载)Pt的比值，P－Δ曲线所计算K的最大值即为该系杆拱桥的稳定安全系数。

图5 主拱肋拱顶截面竖向位移的P－Δ曲线

计算结果表明:考虑几何材料双重非线性的P－Δ曲线和只考虑材料非线性的P－Δ曲线性质基本相同，而得到的几何材料双重非线性稳定安全系数只有10.86，而系杆拱桥第一类稳定安全系数为44.27，其几何材料双重非线性稳定安全系数不足第一类稳定安全系数的1/4。由此可以看出在计算大跨度系杆拱桥稳定安全系数时，几何非线性是次要影响因素，材料非线性是主要影响因素。因此，若要准确得到该系杆拱桥的稳定安全系数，必须要计入材料非线性的影响。

按照上述计算方法也分析了该系杆拱桥在荷载工况2～工况4作用下的非线性稳定性，计算结果表明:该系杆拱桥在这些工况作用下的非线性稳定安全系数相对于第一类稳定安全系数都有相应幅度的降低。