基于岩石应力应变过程曲线的岩爆能量指数法

邓 林，武 君，吕 燕

(1.四川建筑职业技术学院，四川德阳 618000;2.中铁工程设计咨询集团有限公司，北京 100055)

岩爆的机理可以概括为处在一定应力环境中的硬脆性岩石，在外力扰动下使得围岩中积聚的应变能大于克服岩体破坏吸收的能量后使岩石突然以张拉或剪切破坏或张剪复合破坏的形式脱离母岩的一种动力破坏［1-3］。岩体的性质是影响岩爆的重要因素，利用岩石的室内试验分析岩体的工程性质，分析硬岩岩爆倾向性的定量指标是岩爆预测的重要途径。国内外学者根据岩石试验分析岩体能量转移特点，提出了多种能量法预测岩爆，有的研究成果已得到了实际应用［4］，解决了一些生产实际问题，但是这些预测方法往往只考虑了其中的某些单一因素，因此，预测结果与现场实际出现较大的偏差。文章根据岩石的破坏过程中的能量变化和转移，提出了基于岩石变形破坏过程中能量转移特性的岩爆能量指数预测法，并利用雅泸高速公路泥巴山隧道流纹岩进行试验，将该种方法与现有的能量法预测方法进行对比分析，指出了该方法的适用性。结合现场实际情况，提出了定量分析的指标。

1 能量法预测岩爆分析

目前，利用岩石室内试验进行岩爆预测的能量法主要有能量冲击性能指标法和脆性系数指标法、弹性应变能指数法。

1.1 能量冲击性能指标法

岩石的冲击性能指标KE预测岩爆的核心思想是认为只要在开挖过程中岩石吸收的能量大于破坏过程中消耗的能量就发生岩爆［6］。在岩石的单轴压缩的应力应变全过程曲线中，则是以应力峰值为界的左右部分曲线与应变坐标所围成的面积之比。可以用式(1)计算得到岩石的冲击性能指标KE，认为KE＞1时该岩石将发生岩爆。

式中，F1为图1中OAC围成的面积;F2为图1中ACED围成的面积。

图1 能量冲击性能指数法应力应变全过程曲线

显然，F1中包含岩石发生塑性变形和微裂隙发展所消耗的能量，而不是峰值后区岩石破裂所释放的能量。因此，该指标在预测岩石岩爆时夸大了岩爆发生的可能性。

1.2 岩石脆性指标法

岩石脆性指标法的物理意义是岩石脆性越强，岩石破坏的突发性越强［7，8］，即岩石脆性与岩爆有很大的关系，岩石表现出越大的脆性，岩爆的倾向性就越高。而在实际工程中，岩石的脆性大小常简单地用岩石的单轴抗压强度与单轴抗拉强度之比或是用岩石峰值强度前的总变形Lf与永久变形Lb之比来表征，并给出了评价指标，当B=0～0.4，无岩爆，当B=3.5～5.5时，轻微岩爆，当B=5～7.8时，中等岩爆，当B＞7时，强烈岩爆［9-11］。显然这种结论要建立在完整的硬岩中才适用，如在流纹岩及玄武岩这类溢出岩中可能存在隐微的原生柱状节理，因受节理面影响，在试件不同位置进行试验，由试验所得抗拉强度将会相差很大，另外就是在软岩中节理发育的岩石因节理的抗拉强度很低，往往造成抗压强度与抗拉强度比值较大，会造成脆性指数很大的误导。因此，用抗压和抗拉强度之比不能完全反映岩石的弹性变形能的储存能力［8］。这表明用岩石的单轴抗压强度与其单轴抗拉强度之比只能表征结构比较完整的岩石的弹性变形能的储存能力，该方法也夸大了岩爆的可能性。

1.3 弹性应变能指数法

由波兰人A.Q.Kidybinshi提出的弹性应变能指数(Wet)法计算依据如图2所示。

图2 单轴压缩卸荷应力-应变曲线

该理论认为岩爆是围岩在应力调整变化过程中，早期聚集的弹性应变能突然释放的过程［5］。早期集聚的能量大小可以通过单轴压缩卸荷试验得到的卸荷应力-应变曲线进行分析，即可以采用应力应变曲线分析在变形过程中损失的能量，可以恢复的弹性变形能与产生塑性变形损失的能量之比表征岩爆发生的可能性，可用公式(2)表示。

其式中，φsp为岩石破坏峰值强度前储存的弹性应变能，即图1中AOC围成的面积;φst为耗散的应变能，即图2中AOB围成的面积。

该指标将峰值前岩石储存的能量分为弹性变形能和塑性变形能，反映了岩石弹性变形能的储存能力，在一定程度上反映岩石破坏时的能量释放大小，波兰等国家将其作为了国家标准，给出了定量预测的指标，当Wet＜2.0时，不会产生岩爆，当Wet=2.0～4.9时，中、低强度岩爆，当Wet≥5.0时，严重岩爆。但是该指标并没有涉及岩石峰值强度后的应力变化情况，不能完全反映岩石破坏后区的能量释放和动力破坏所需能量之间的相对关系，不能确定岩体是突然破坏还是持续稳定破坏，因此不能完全反映岩爆的倾向性的真实情况。

1.4 岩爆能量指数法分析

尽管现在的能量法预测岩爆解决了一些生产问题，但从前面的分析可以看出，能量冲击性能指标法、岩石脆性指数法及弹性应变能指数法都只考虑到其中的某一方面的因素，并且受试验条件等因素影响，很多时候也出现了较大的偏差。将以塑性变形为主的黏性土和以弹性变形为主的典型的硬脆性岩石单轴压缩曲线进行对比分析可知，黏性土压缩变形曲线峰值强度后曲线多近似为一水平线，而对于岩石应力应变全过程曲线则是随着硬脆性的变化发生显著变化，对于软岩的变形曲线则与黏性土接近，而对于硬质性脆的岩石则峰值强度后的曲线似F密度分布曲线，即峰值强度后岩石有一部分弹性变形能。国内外学者经过大量岩石试验也证明应力应变全过程曲线在峰值强度后区为F密度分布曲线的岩石往往会产生岩爆［12］。基于此，可以在刚性试验机上对岩石进行单轴压缩试验，获取应力应变全过程曲线，重点分析应力应变全过程曲线峰值强度后段应力应变过程曲线，找出弹性变形与塑性之间的关系，即可以找出剩余弹性变形的能量与克服裂隙扩张消耗的塑性变形能之间的关系用以表征岩爆烈度——岩爆能量指数法，其评价依据如图3所示。

由前面的分析可得，如果岩石处于稳定塑性流动变形状态，则其变形曲线在峰值强度后为一条平行于应变轴的水平线(如图3中AF线段)，即岩体的内部结构为一个动态稳定结构，继续加载吸收的能量就全部转化为岩石塑性变形消耗的能量，岩石不发生突然破裂或破坏。如果应力应变全过程曲线在峰值强度后逐渐下降，如图3中的AD、ACD'线段，则加载输入的能量就有一部分转为恢复弹性变形的能量，一部分用于消耗裂隙继续扩张塑性变形的能量，说明岩石峰值强度前吸收的能量大于岩石峰值强度后塑性变形所消耗的能量，即有剩余弹性变形能。如果隧道开挖后提供有临空面，剩余的弹性变形恢复，岩石以岩爆的形式出现以适应应力的调整，多余弹性变形能与克服塑性变形消耗的能量之间的大小关系则可以反映岩石发生破坏的强烈程度。其计算公式如式(3)所示。

图3 应力应变全过程曲线示意

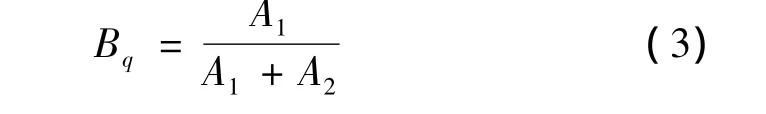
式中，Bq为岩石岩爆能量指标;A1为ADF围成的面积;A2为CADE或CAD'E围成的面积

显然Bq是一个小于等于1的数据，考虑到无岩爆与强岩爆是两种极端情况，将这两种边界指标波动范围划得偏小，其余的两种情况按中间等分划分，采用如下判别标准进行岩爆预测:

当Bq=0～0.20时，无岩爆;

当Bq=0.20～0.50时，弱岩爆;

当Bq=0.50～0.80时，中等岩爆;

当Bq=0.80～1.00时，强岩爆。

2 试验分析

采用泥巴山隧道勘察钻孔岩芯制作试样，进行室内单轴压缩条件下的荷载-应变全过程试验与峰值前的加-卸载试验，试验在MTS815程控伺服刚性试验机上进行。试样为流纹岩，岩性致密坚硬，加工成φ50 mm×100 mm的圆柱试件，典型的应力-应变全过程曲线如图4所示。

图4 典型应力-应变全过程曲线

为了比较采用能量指数Ba与能量冲击指标KE和能量指数弹性变形能指数Wet几种能量法预测岩爆的异同，根据室内岩石单轴压缩和卸载所得应力－应变全过程曲线，采用前述的公式(1)、公式(2)、公式(3)进行计算，并与现场实际发生的情况进行比较分析。将计算结果列于表1中。

表1 能量法分析预测结果

根据表1可知，该隧道开挖的过程中将会发生岩爆，采用不同的判别标准结果相差较大。到现在隧道即将贯通时，采用岩爆能量指数法与现场比较吻合，采用弹性变形能指数法、冲击指标法、脆性指标法均夸大了岩爆的烈度。

3 结论与展望

(1)采用冲击指标法、脆性指标法都放大了岩爆的烈度，夸大了岩爆的可能性。

(2)采用岩爆能量指数法克服了变形能指数法不考虑峰值强度后的变形，可以判定是发生岩爆还是塑性变形。

(3)提出的岩爆能量指数法考虑了岩体的峰值强度后能量的存储与转移，克服了冲击指标法、脆性指标法不考虑破坏阶段进一步变形吸收的能量，更能反映岩爆的可能性，且试验简单。

(4)利用岩爆能量指数法判别岩爆是利用大相岭泥巴山隧道的流纹岩进行试验并结合现场实际发生情况提出的，具有一定的参考价值，但是试验数据还不多，还需要进一步试验修正。

［1］Lin Deng，Yan Lv，Deng Ronggui.Present Situation and consideration of Rock Burst Hazard，Advanced Materials Research，Vols.250－253，2011:136-147.

［2］徐则民，黄润秋.长大隧道岩爆灾害研究进展［J］.自然灾害学报，2004，13(2):16-24.

［3］马少鹏，王来贵，章梦涛，等.加拿大岩爆灾害的研究现状［J］.中国地质灾害与防治学报，1998，9(3):107-112.

［4］徐士良，朱合华，丁文其，等.秦岭公路隧道通风竖井岩爆预测和防治措施［J］.岩土力学，2009，30(6):1759-1763.

［5］Kidybinski A.Bursting liability indices of coal［J］.Rock Mech.and Min.Sci.1981，18(6):295-304.

［6］赵本钧.冲击地压及其防治［M］.北京:煤碳工业出版社，1995.

［7］李廷芥，王耀辉，张梅英，等.岩石裂纹的分形特性及岩爆机理研究［J］.岩石力学与工程学报，2000，19(1):610.

［8］唐礼忠，王文星.一种新的岩爆倾向性指标［J］.岩石力学与工程学报，2002，21(6):874-878.

［9］Dowding C H，Andersson C A.Potential for rock bursting and slabbing in deep caverns［J］.Engineering Geology，1986，22:265-279.

［10］徐林生，王兰生.二郎山公路隧道岩爆发生规律与岩爆预测研究［J］.岩土工程学报，1999，21(5):569-572.

［11］Donll.Vibrations studies:blasting and rock bursts［J］.Canandian Mining and Metallurgical Bulletin，1951，470:415-418.

［12］蔡朋，邬爱清，汪斌，等.一种基于Ⅱ型全过程曲线的岩爆倾向性指标［J］.岩石力学与工程学报，2010(S1):3290-3294.