瞬态热量标定系统的太阳模拟器光学系统设计

顾国超，王 丽，刘洪波，高 雁，陈家琦

(中国科学院长春光学精密机械与物理研究所，吉林长春130033)

1 引言

太阳模拟器有集中式和非集中式两种应用方式。前者的特征是在大接收面上提供光谱、均匀性、准直角、能量等各方面都与太阳光相近的辐照，主要用来测试太阳电池光伏特性或做热真空试验，如德国和欧州航空局在1983年建成的太阳模拟器［1-2］以及国内的KM系列太阳模拟器;而后者的特征则是将太阳能聚焦在一个非常小的面积内，达到极高的温度，主要应用于测试部件的高温特性和热化学特性，如Ulmer S和Patrick Coray等人分别利用了相似的结构在一个小接收面上得到了极高的能量［3-4］。

本文所设计的太阳模拟器服务于某种瞬时热量标定系统，在较小的接收面上不仅需要较高的能量输出，对其均匀性也有着非常高的要求。上述两种系统均能满足部分要求，但难以兼顾。高雁等人采用了与Ulmer S的设计相似的聚光系统，配合一个带锥角的通道反射式积分器，在一定程度上兼顾了能量和均匀性［5］;盛益强和王素平等人分别采用了未带锥角的通道反射式积分器进行匀光，均匀性达到了较好的效果［6-7］。综合考虑，本文的设计采用短弧氙灯作为光源，利用椭球聚光镜进行聚光，并配合一个未带锥角的通道反射式积分器进行匀光。文中对椭球聚光镜和通道反射式积分器进行了分析，优化了整个系统，结果显示其能量和均匀性都很好地满足了使用要求。

2 光学设计

2.1 原理及设计指标

本文采用的总体布局如图1所示，主要由短弧氙灯、椭球聚光镜和光学积分器组成。椭球聚光镜第一焦点附近的氙灯氙弧发出的光经反射后汇聚于第二焦点，并耦合进光学积分器内部，不同角度的光经内壁反射后混合叠加，照射在距积分器输出端给定距离的辐照面上，从而得到均匀的光能分布。主要技术指标如表1所示。

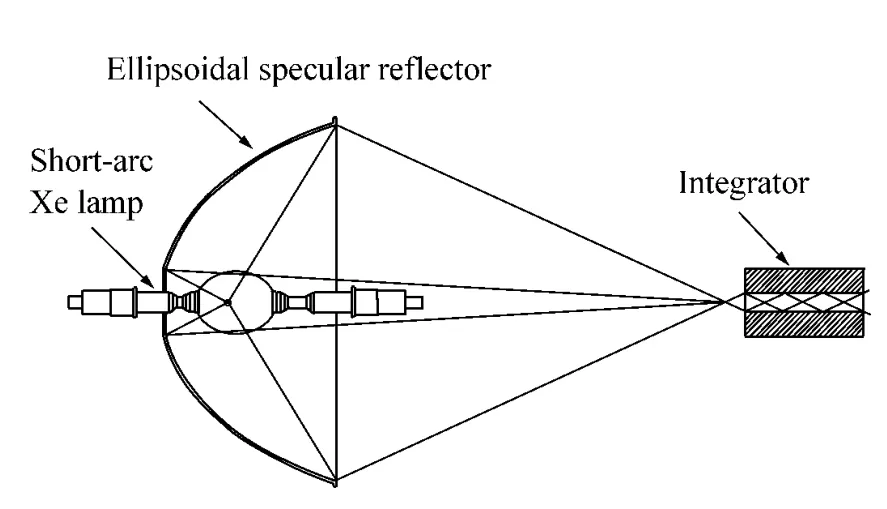
图1 光学布局Fig.1 Layout of optical system

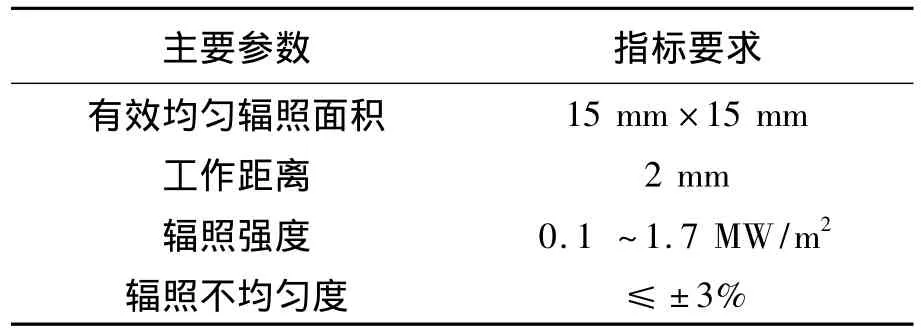
表1 主要技术指标Tab.1 Main technical index

2.2 光源选择

由于氙灯的光谱与太阳光谱近似，故太阳模拟器所选择的光源通常是高功率氙弧灯，也有部分模拟器采用氩弧灯、卤钨灯或其他灯具。本文利用了OSRAM公司提供的7 000 W氙灯，其发光亮度分布如图2所示，配光曲线如图3所示。

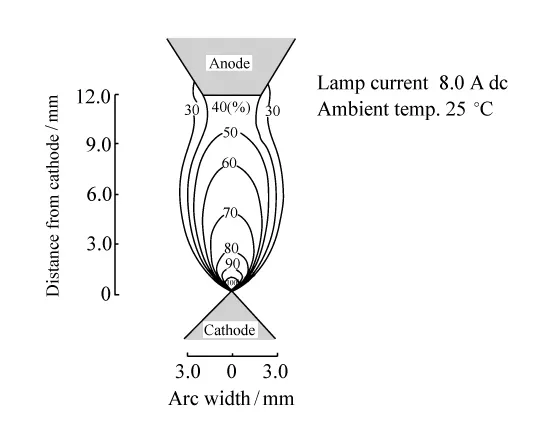
图2 氙灯发光亮度分布Fig.2 Intensity distribution of Xe arc

图3 氙灯配光曲线Fig.3 Flux distribution of Xe arc

2.3 聚光镜设计

聚光镜的作用一方面在于尽可能地将光源发出的光汇聚于第二焦点并耦合进积分器内部，另一方面则是在积分器入口端提供适宜的辐通量角度分布(对通道反射式积分器而言)。这将决定系统辐照能量和均匀性两个最重要的技术指标，因此椭球镜的设计优劣可以由以下指标确定:

(1)聚光效率

聚光效率是聚光镜所汇聚的能量占光源发出的总能量比率。可由式(1)和(2)来表示:

式中:Kc为聚光效率;t(u)为光源辐射强度角度分布;I0为光源法向发光强度;I(u)为光源在u角方向上的发光强度;α和β的定义如图4所示，且在实际计算中t(u)由实际测量的氙灯配光曲线(数据)给出。

(2)积分器孔径利用率

积分器孔径利用率K1取决于第二焦面上的辐通量相对分布，与氙灯的离焦量、氙弧大小、聚光镜近轴放大倍率等因素相关。

(3)积分器入射端辐通量角度分布

积分器入射端辐通量角度分布影响系统的均匀性和能量两方面，但影响并不直观，因此聚光镜的设计主要考虑其聚光效率和孔径利用率两方面。

对于聚光镜的设计，采用图4所示的坐标系，椭球聚光镜外形尺寸由下述方程表示［8］:

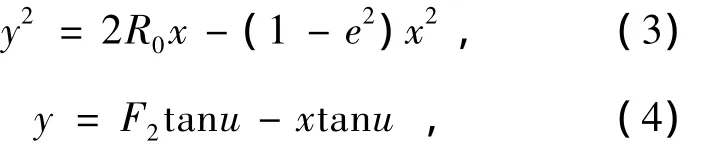
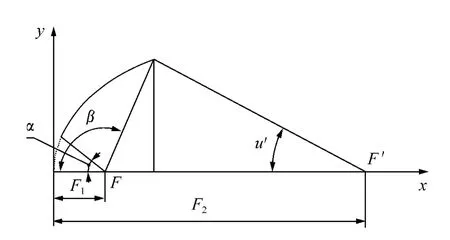
图4 椭球聚光镜光学参数Fig.4 Optical parameters of ellipsoidal specular reflector

综上所述，聚光镜的设计应在尽量满足较高的聚光效率和口径利用率的前提下，设计一系列的聚光镜，使得第二焦面上产生不同的辐通量角度分布，并优选出适合的聚光镜参数。其设计准则如下:

(1)选择合适F1值，使得氙灯安装时泡壳不与椭球镜干涉，并有足够的散热空间;

(2)图3所示的氙灯配光曲线显示其发光区域处于20～135°，因此聚光镜的反射区应包容此区域;

(3)由于氙灯氙弧具有一定大小，因此应优选近轴放大倍率M0，使得氙弧经放大之后能够落在积分器入射端的通光口径内;

(4)如图1所示，由氙弧所发角度α的光反射后应避免照射在灯体上，以免其过热并影响使用;

(5)设计一系列聚光镜，以得到不同的u角和辐通量角度分布。

综合考虑各方面因素，选取焦距F1=140，近轴放大倍率M0=3～5.5的椭球镜系列作为反射聚光镜，如图5所示。

图5 椭球镜系列Fig.5 Arrays of ellipsoidal specular reflector

2.4 光学积分器分析与设计

通道反射式的积分器就是使光线经内壁面的多次反射，将光束以积分器端面的形状出射，其作用就如一个扰频器，能够改变光束的亮度分布，使得亮度分布不均的入射光束经光学积分器后，均匀性大幅提高，如图6所示。

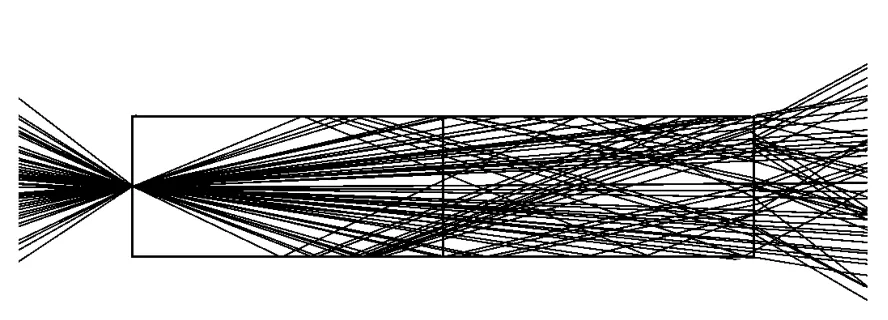
图6 光学积分棒中的光线传输Fig.6 Light transmitting in integrator

假设氙弧经聚光镜成像后在第二焦面上形成一个半径为R的圆盘形光源，在±φmax角度范围内(φmax为图4中所示的孔径角u)光亮度为L，在±φmax角度范围以外的光亮度L=0。光源处于端面边长均为b，长度为l的积分器入口处，如图7所示，则输出平面上某给定位置照度值就等于各角度输入亮度值乘以标准余弦权重因子的积分值［9］:

当光线从光源出发，以参数θ，φ入射时，亮度为L(θ，φ)，当光线从光源和积分器之间的缝隙中入射时，亮度为0。

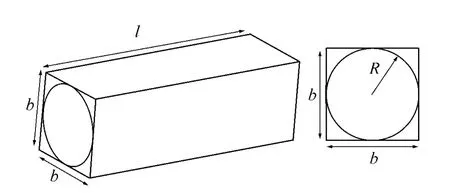
图7 积分器和光源的尺寸Fig.7 Sizes of integrator and light source

图8 光学积分器成像方法示意图Fig.8 Schematic illustrations of imaging method with lightpipe

图9 出射面照度分布原理示意图Fig.9 Schematic illustration of intensity of illumination distribution

本文所用的积分器端面为正方形，利用镜面成像的方法很容易确定到达被照面上的光线是否从光源发出。如图8(a)所示，A为实际光源，A1为经积分器顶反射面反射一次所形成的光源像，A2为经顶、底面反射两次所形成的光源像;当光线经顶、底面多次反射时，能够形成一列线性虚拟光源;若光线经积分器周边4个面反射时，则会形成一列二维光源阵列，如图8(b)所示。由于反射壁面为平面，互相垂直且正交于光源面，因此所形成的二维光源阵列处于同一平面内，且排布规则。若忽略反射损失，并假设光源没有±φmax孔径角的限制或积分器无限长，则此二维阵列为无穷的。事实上经聚光镜反射后所形成的光源具有一定的孔径角，则虚拟光源阵列为有限的，如图9所示，棱锥的半角为φmax，出射面上的光照度就是棱锥底面上的光源共同照射、互相叠加的结果。参与照射的光源数量与反射次数相关，其关系如图10所示，若反射次数为F，则光源阵列数为(2F+1)2。反射次数越多，参与照射和叠加的光源就越多，输出面照度分布就越均匀，但同时也意味着反射损失会增大，从而使得接收面光能减少，因此积分器的设计应在满足输出面光能大小的前提下，使得反射次数尽可能多，即选择尽量长的积分器以及增大聚光镜的孔径角。

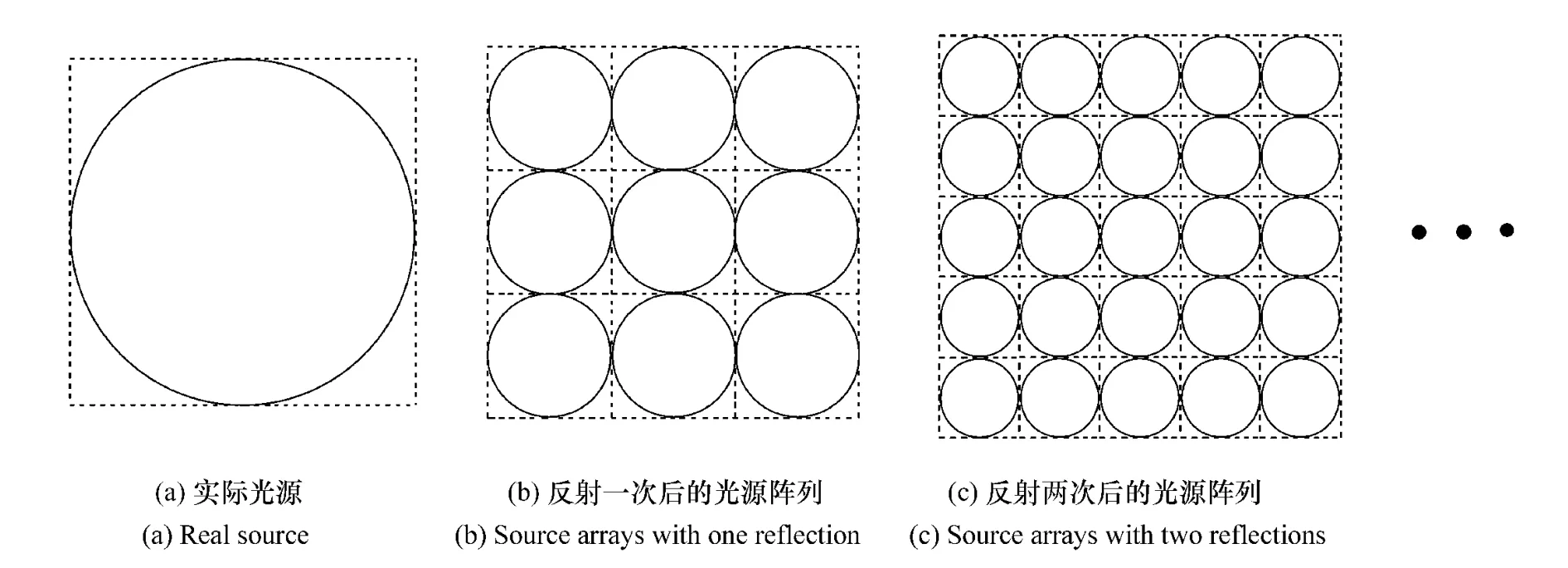
图10 反射次数与光源阵列关系图Fig.10 Relationship between reflection and source arrays

2.4.1 积分器输出照度体均匀性分析

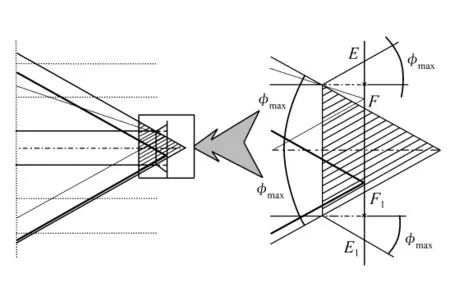
图11 积分器输出光体均匀性分析Fig.11 Spatial uniformity of integrator

若积分器足够长，则光源阵列面上的亮度不均匀性就可以忽略，此时输出端各点照度只与所对应的照射面积相关。如图11所示，平面EE1距出射面有一定距离，若EE1上的点处于FF1之间，以其为顶点，半角为φmax，可形成一底面处于光源面内的圆锥体，则整个椎体底面均为照射面积;若点位于EF或E1F1之间，则椎体底面只有部分为照射面积，且点越接近E或E1，照射面积就越小;若点位于点E或点E1之外，则照射面积为0。故面EE1上FF1之间的区域为均匀的，相应的，图11中阴影部分以及图9中以出射端面(绿色面)为底面，以棱锥顶点为顶点的小棱锥部分为均匀区域。

为了验证以上分析的正确性，取积分器尺寸为20 mm×20 mm×100 mm，光源为R=10 mm的面光源，入射角度为±45°，功率为1 W，利用Light-Tools中的蒙特-卡洛光线追迹方法，追迹100万条光线，所得结果如图12所示。

以上述所设参数为准，建立体均匀性棱锥，依图12中所给位置将棱锥切片，并将切片区域与蒙特-卡洛追迹结果进行对比，可知两者是统一的。

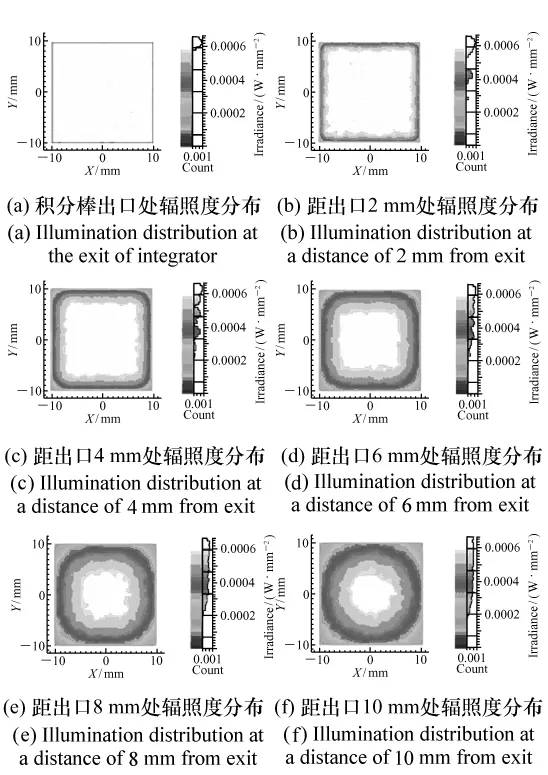
图12 仿真结果图Fig.12 Simulation results

2.4.2 光学积分器输出照度理论分析

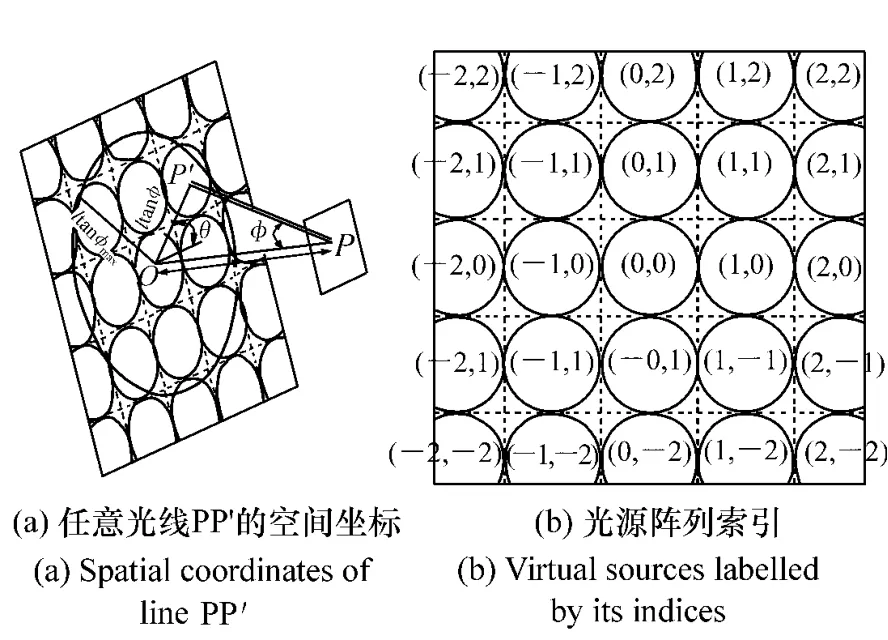
图13 空间坐标和光源索引Fig.13 Spatial coordinates and source indices

为求得接收面上某点P的照度值，可将其沿直线反向追迹到光源阵列面上，方法如图13(a)所示，各光源依据反射次数给予(i，j)的标签，方法如图13(b)所示，其中标签为(0，0)的是实际光源，其余为镜像所成的虚拟光源，这样可知各虚拟光源相对于点P的位置。当一条直线以参数(θ，φ)入射在点P，则其在光源平面内所对应的点具有极坐标(r，θ)=(ltanφ，θ)，故式(5)可化为各单独光源的积分形式。由于镜面反射出射角和入射角相等，故在光线传播过程中φ保持不变。因此若φ＞φmax，L=0，相应的在光源阵列平面内只能计算半径ltanφmax内的光源的积分，如图13所示，设积分器内壁面的反射率为ρ，则等式(5)变为:

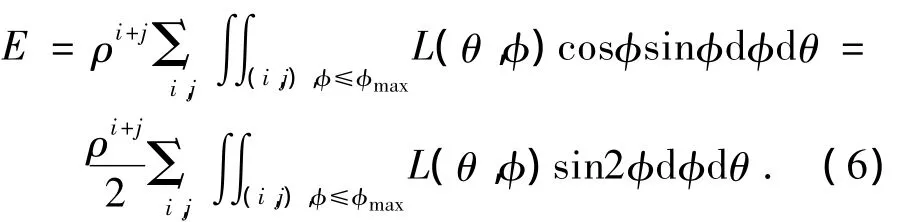
在满足附加条件φ≤φmax情况下，各积分(i，j)由相应的光源边界而定，若已知聚光镜反射后积分器入射端的亮度分布情况L(θ，φ)，可以计算积分器出射端任一点的照度情况，但由于系统的复杂性，要计算出L(θ，φ)非常困难，因此对积分器的分析只能通过蒙特-卡洛追迹法进行仿真。

2.4.3 光学积分器参数选择

依据系统有效均匀辐照面积，选定积分器通光口径为20 mm×20 mm的正方形，考虑积分器所放置的罐体大小以及罐体内部各设备空间干涉问题，确定积分器的外形尺寸为100 mm×100 mm ×l，其中长度 l≤90 mm。

3 系统仿真

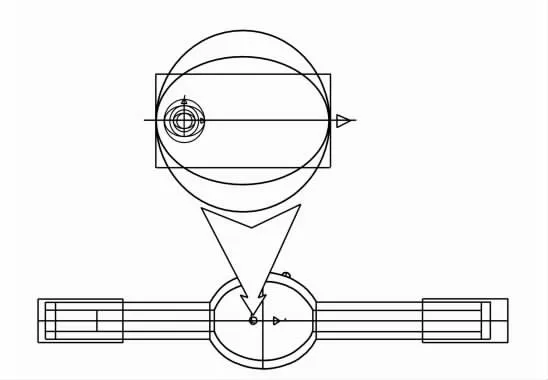
图14 灯体建模图Fig.14 Model of light

采用Light-Tools软件中的蒙特-卡洛追迹方法对系统进行仿真，光源模型以厂家所给的发光体模型、光能分布权重以及空间角度分布数据为准，采用模型嵌套和Apodizer功能实现，所得结果和配光曲线如图14和图15所示。

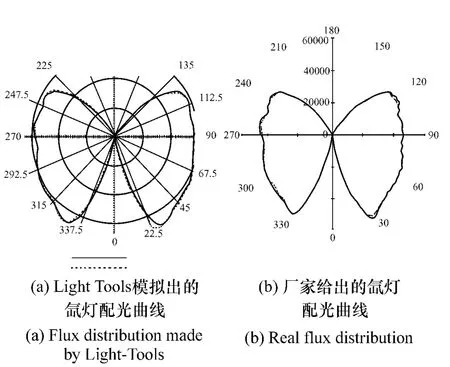
图15 配光曲线对比图Fig.15 Comparison of flux distribution curves

取聚光反射镜和积分器通道壁面反射率均为ρ=0.86，以图1所示的布局对系统进行建模，追迹500万条光线，以代表其均匀性，则结果如图16所示。

图16 均匀性仿真结果Fig.16 Simulation results of uniformity

图中结果显示，均匀性整体趋势随积分器长度增长而变好，但过程中出现振荡，甚至出现长度更长时均匀性反而较差的情况。这种现象可以通过研究光源面内的照射面积，即半径为ltanu的圆形区域来解释。此区域随着l的增大而扩展，当区域边缘通过各光源中心时，照度值达到峰值;若通过各光源间空白地带中心，则照度值会处于谷值。以中心和角落点为例，如图17所示，对中心点而言，当区域边缘处于a位置以内或c位置时，照度值处于峰值，b位置则对应着谷值;角落点的d和f位置对应谷值，而e位置对应峰值。因此随着管长的增长，两处照度值均会呈现振荡，且为反相，因此均匀性亦会随之振荡;且随着边缘扩张，通过光源中心和空白中心的频率会越来越快，照度变化也越来越小，因此整体均匀性会越变越好。

图17 中心和角落点光锥底面变化趋势Fig.17 Alteration by circles of radius ltanφmaxabout center and corner

以P代表接收面上的接收能量，则能量特性如图18所示。

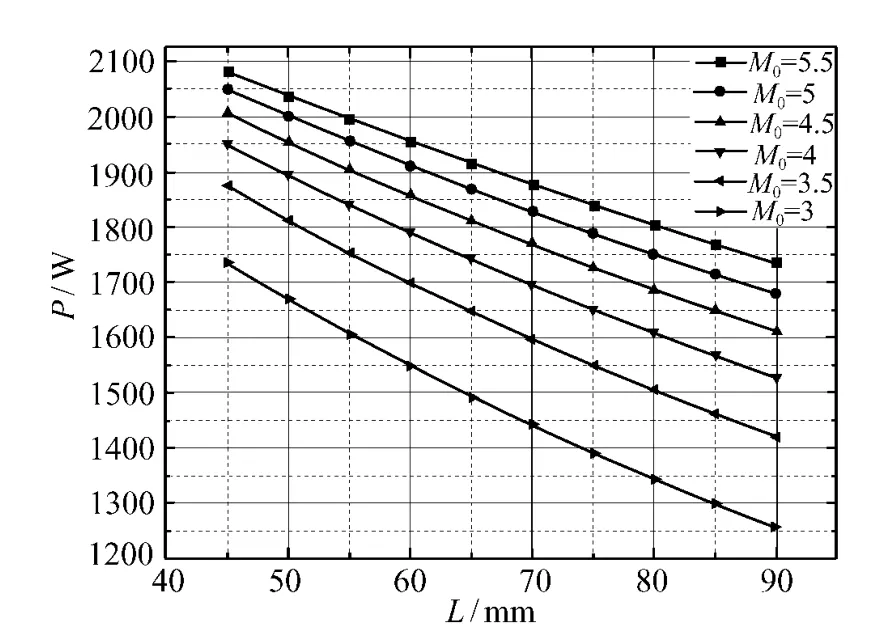
图18 能量特性仿真结果Fig.18 Simulation results of energy

图中结果显示:能量随积分器长度的增长以近似线性的方式下降;对不同聚光镜而言，近轴放大倍率越小，能量越低，且随着放大倍率的降低下降速度越来越快。这是由于聚光镜反射区域要包容20～135°区，孔径角u会随着放大倍率的降低而增大，如图19所示，这使得积分器通道内反射次数激增，故能量迅速下降。相应的，参与照射叠加的光源数目也会迅速增加，这也意味着均匀性的变好，这与图16中表现的特性相符。

图19 孔径角随放大倍率变化图Fig.19 Relationship between aperture and magnification

图16中结果显示，当 M0=4.5、L=85 mm，M0=4、L=75 mm，M0=3、L＞83 mm 时，均匀性都在4%以下，综合考虑其稳定性(观察所选点的斜率)和接收能量，选取参数M0=4.5，L=85 mm，此时均匀性达到了3.8%，能量为1 650 W，平均辐照度为4.125 MW/m2，即4 125个太阳常数(AM1.5标准:1太阳常数 =1kW/m2)。将氙灯稍微离焦，则均匀性能够在3%以内，且能量没有明显下降，这种状态完全能够满足均匀性为3%，辐照度为100 kW/m2～1.7 MW/m2的要求，若将光源换成5 000 W氙灯，均匀性几乎没有变化，能量为1 192 W，此时辐照度为2.98 MW/m2，达到了2 980个太阳常数，同样满足使用要求。

4 结论

本文对一种用于瞬时热量标定系统的太阳模拟器的光学系统进行了设计和分析，选择OSRAM公司提供的短弧氙灯，并确定第一焦距 F1=140 mm，设计了不同近轴放大倍率的椭球聚光镜，以得到不同聚光效率、辐通量利用率和孔径角。分析了通道反射式积分器的工作原理、体均匀性、以及接收面各点照度的理论计算方法;利用Light-Tools软件中的蒙特-卡洛方法对系统进行了仿真并分析结果，优选了M0=4.5，L=85 mm的系统。结果显示，若系统采用7 000 W氙灯，可得到3%的均匀性和4 125个太阳常数的辐照强度;若采用5 000 W氙灯，可得到3%均匀性和2 980个太阳常数的辐照强度，两者均满足使用要求。

［1］ FEIL O G，FREY H U.Solar simulation with rectangular beam［C］.Proceedings of the 15th Space Simulation Conference，Nov.1-3，1988，Williamsburg，Virginia，USA，1988:278-288.

［2］ BRINKMAN P W.Main characteristics of the large space simulator(LSS)at ESA/ESTEC［C］.Proceedings of the 13th Space Simulation Conference，NASA CP12340，Oct.8-11 Orlando，Florida，USA，1984.

［3］ ULMER S，REINALTER W，HELLER P，et al..Beam characterization and improvement with a flux mapping system for dish concentrators［J］.Sol.Energy Eng.，2002，124(2):182-188.

［4］ PETRASCH J，CORAY P，MEIER A，et al..A Novel 50 kW 11 000 suns high-flux solar simulator based on an array of xenon arc lamps［J］.J.Solar Energy Eng.，2007，129:405-411.

［5］ 刘洪波，高雁，王丽，等.高倍聚光太阳模拟器的设计［J］.中国光学，2011，4(6):594-599.LIU H B，GAO Y，WANG L，et al..Design of high-flux solar simulator［J］.Chinese Optics，2011，4(6):594-599.(in Chinese)

［6］ 盛益强，方志良，母国光，等.投影电视的均匀照明系统设计［J］.光电子·激光，2004，15(4):416-419.SHENG Y Q，FANG ZH L，MU G G，et al。.Design of illumination systems for projection displays［J］.J.Optoelectronics·Laser，2004，15(4):416-419.(in Chinese)

［7］ 王素平，凌健博，刘立伟，等.一种应用于太阳仿真器的照明系统设计［J］.光电工程，2006，33(9):32-34.WANG S P，LING J B，LIU L W，et al..Simple lighting system applied to the solar simulation［J］.Oplo-Electronic Eng.，2006，33(9):32-34.(in Chinese)

［8］ 罗青青.宽光谱太阳模拟器的理论分析与整体设计［D］.天津:天津大学，2009.LUO Q Q.Theoretical analysis and integral design for wide spectrum solar simulator［D］.Tianjin:Tianjin University，2009.(in Chinese)

［9］ 张以谟.应用光学［M］.北京:电子工业出版社，2008.

ZHANG Y M.Application Optics［M］.Beijing:Publishing House of Electronics Industry，2008.(in Chinese)