脉冲型近断层地震动作用单自由度体系响应分析1

郭 靖 陈健云 何 伟 徐 强

1）大连理工大学工程抗震研究所，大连 116023

2）大连理工大学海岸与近海工程国家重点试验室，大连 116023

引言

近断层地震动能够对城市基础设施造成比远场地震动更严重、更复杂的破坏，已经引起国内外建筑工程界的广泛关注（李明等，2010）。近断层地震动与远场地震动存在明显的差异，作为主要因素的方向性效应越来越得到研究者的重视。方向性效应是由于断层破裂速度接近剪切波的传播速度引起的，在地震记录中表现为速度时程中含有大幅值，短持时的速度脉冲，如图1所示。由于前方向性效应更容易引起结构的破坏，所以通常方向性效应多是指前方向性效应（胡进军，2009）。

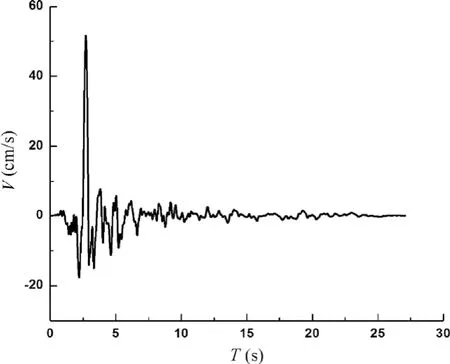
图1 近断层地震动速度时程Fig. 1 Velocity time history of near-fault ground motion(Gilroy Array #6, Coyote Lake, 1979)

本文根据所选取的 40条近断层地震动记录，采用小波分析方法将初始记录分解，得到脉冲波部分和高频波部分，分析单自由度弹性体系和非弹性体系在两部分波作用下的响应，并指出仅仅用速度脉冲模拟近断层地震动存在局限性。

1 小波分析分解地震动记录

1.1 近断层地震动分析模型

针对近断层地震动存在速度脉冲的特性，以往的研究大多集中于建立等效的速度脉冲模型来模拟近断层地震动，忽略了频率相对较高的非脉冲部分（即高频部分）。Krawinler等（1998）用三角形模型进行模拟，并且提出分别包含1、2、5个半速度循环的脉冲模型；Menun等（2002）基于非线性回归分析提出一种五参数模型；我国学者李新乐等（2004）在Menun等（2002）模型的基础上提出了相应的等效速度脉冲模型；Mavroeidis等（2004）的研究结果表明，高频波部分同样对结构产生重要影响，仅仅用等效脉冲模型进行分析存在缺陷。

Jack（2007）用小波分析方法对近断层地震动进行定性识别，通过从地震波记录中提取出速度脉冲，并根据脉冲波速度峰值与初始波速度峰值的比值，确定某地震动是否是近断层地震动（Jack, 2007；Ghaghara等，2010）。该方法的实质是将近断层地震动分解，提取出的速度脉冲波部分作为等效速度脉冲模型，而剩余部分相对于脉冲波部分而言频率较高，称为高频波部分（即非脉冲波部分）。本文采用小波分析对记录的地震波进行分解，同时对得到的脉冲波部分和高频波部分进行分析。

1.2 近断层地震动数据选取

Jack（2007）通过对大约3500条地震动记录进行分析，确定出91条含有速度脉冲，可视为近断层地震动的地震波记录，然而该方法在分析过程中并没有排除多脉冲地震波记录。产生多脉冲波动的原因很复杂，如：盆地和凹凸地貌等（Stewart等，2001)，所以仅根据Jack（2007）的方法还不足以准确地判定脉冲是否由方向性效应引起的。

本文在分解地震波过程中，为了排除多脉冲地震动记录，补充了以下2个附加条件：（1）提取速度脉冲后，对剩余地震动记录用小波分析方法再次进行分解，要求所得的速度脉冲峰值小于30cm/s。因为较低强度的地震动可能因为速度时程的单一而出现脉冲，30cm/s可以作为排除脉冲的一个临界标准（Jack，2007）。

（2）剩余部分的速度峰值虽然大于30cm/s，但与初始地震动的记录峰值相比小于30%。

通过重新计算Jack（2007）所确定的地震动记录，得到 40条记录满足上述条件，作为本文计算所使用的地震波。

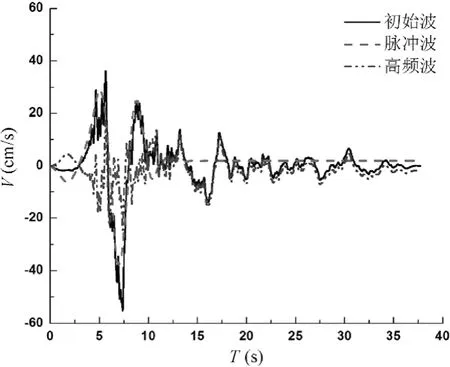
图2 小波分析方法分解算例Fig. 2 Example of decomposition result using wavelet analysis (Holtville Post Office, Imperial Valley-06, 1979)

1.3 分解算例

算法选用 Daubechies小波基（db4），连续小波变换的分解算例结果如图2所示。

2 单自由度弹性体系响应

图3为单自由度体系伪加速度反应谱分析算例，可以看出用小波分析分解所得的脉冲和高频两部分波对不同周期结构的影响，在较低周期范围（如周期T<1s）内，在高频波作用下结构的响应相对于脉冲波所得结果更接近结构在初始地震波激励下的响应；而在较长周期范围内，脉冲波的计算结果更为精确。在近断层地震动作用下，分析弹性体系的响应应该分成两部分，即针对长周期的结构脉冲波部分将起到主导作用，而高频波部分将对短周期结构产生显著影响。

图3只是定性地给出了脉冲波和高频波对于不同周期范围结构的影响的差异，本节将通过计算所选取的40条地震波，用统计的方法定量地分析脉冲波和高频波两部分起主导作用的结构固有周期范围。

计算选取结构阻尼比ζ = 0.05；将脉冲波和高频波的伪加速度反应谱结果分别用初始地震波计算结果进行归一化处理，同时将结构的固有周期T用初始地震波的速度脉冲周期Tp进行归一化处理，以表示结构固有周期与小波分析所得速度脉冲周期的关系。可以推断，所得曲线上各点的纵坐标越接近于 1，表明越接近于初始地震波的结果。归一化计算范例如图4所示，可以看出，脉冲波和高频波两部分的作用反应曲线存在一个交叉点（大约在T/Tp=0.5附近），表明结构的固有周期如果大于该点对应的周期，脉冲波部分将对结构的响应起主导作用，反之高频波部分将起主导作用。转折点对应的周期本文称为临界周期。

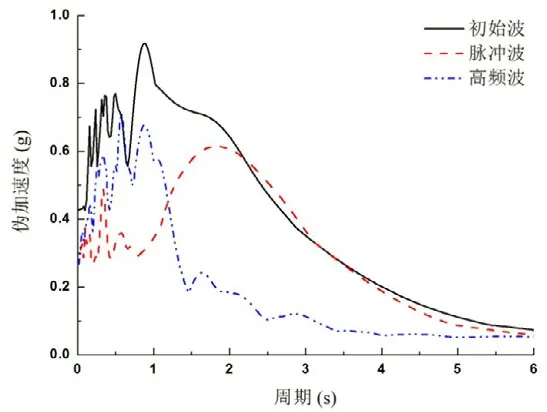
图3 伪加速度反应谱算例Fig. 3 Example of pseudo-acceleration response spectra (Newhall-West Pico Canyon Rd,Northridge-01, 1994)

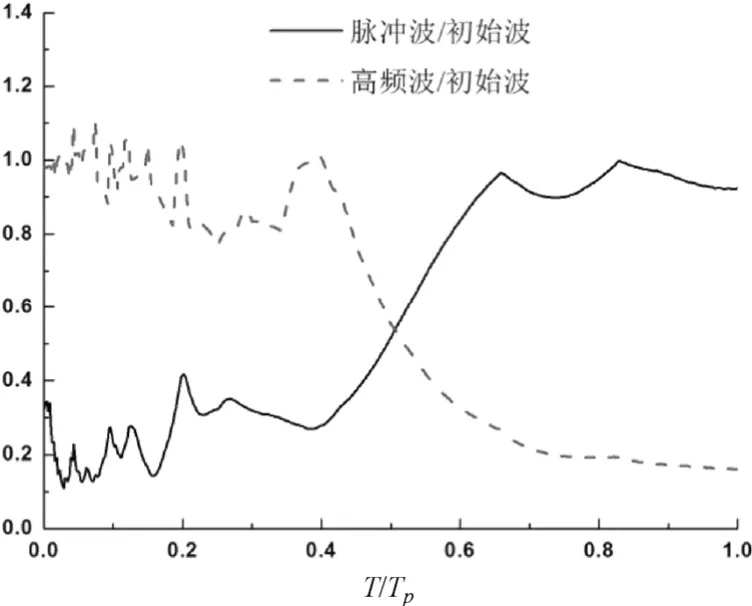
图4 地震波算例归一化伪加速度反应谱Fig. 4 Example of normalized pseudoacceleration response spectra(TCU087, Chi-Chi Taiwan, 1999)

统计全部40条地震波的计算结果（地震波EI Centro Array#3和Napa Fire Station #3的结果曲线在 T/Tp=0.5附近产生交叉波动，故取平均周期），脉冲周期与临界周期的拟合曲线如图5所示。从图5可以看出，临界周期一般为速度脉冲周期的0.484倍左右，该结果比Ghaghara等（2010）的结果（0.38）要大些，因为Ghaghara等（2010）选用的地震动并没有排除多脉冲振动响应的影响，因此脉冲波部分影响的周期范围要稍大些。

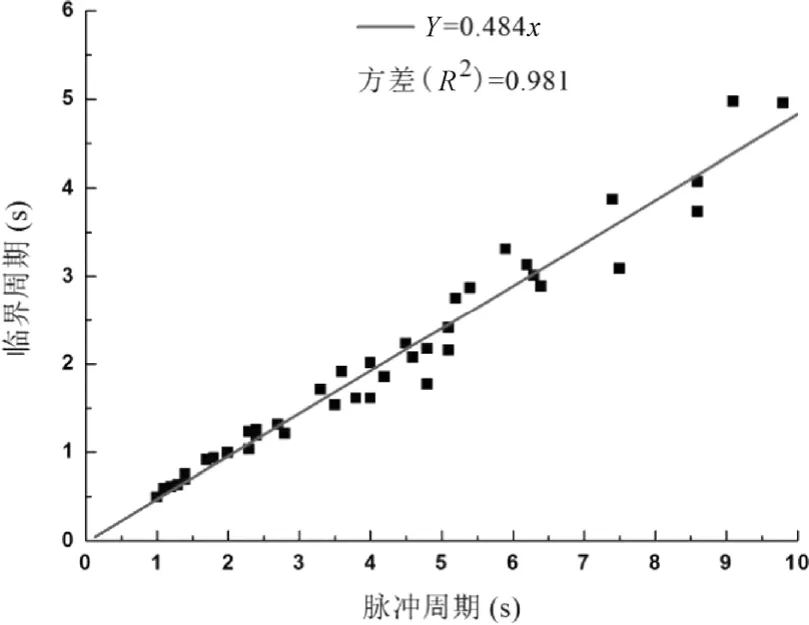
图5 脉冲周期与临界周期拟合结果Fig. 5 Curve fitting of threshold period versus pulse period

从计算结果可分析出，在进行近断层地震动分析时，高频波部分同样将对一定固有周期内的结构产生重要影响，尤其是固有周期小于临界周期的结构。本文在此处验证了Mavroeidis等（2004）的结论。

3 单自由度非弹性体系响应

本文采用简化的弹塑性模型（谢礼立等译，2007）分析单自由度非弹性体系反应，如图6所示。其中，f0，u0分别为对应的线性体系中地震动引起的抗力和变形的峰值；fy，uy分别为屈服强度和屈服变形；um为弹塑性体系的位移峰值。将um用uy进行标准化后所得到的无量纲比值称为延性系数，即：

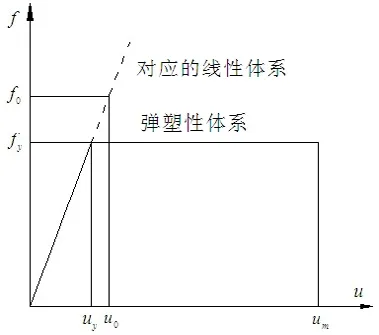
图6 非弹性体系分析模型Fig. 6 Inelastic system model used in analysis

在已知某延性系数的情况下，屈服位移和周期的关系称为等延性反应谱，根据式（1），求出施加在非线性体系上的位移需求。

本文的计算选取μ=2,4,8，ζ=0.05；分别将脉冲波和高频波的计算结果用初始地震波计算结果进行归一化处理，并将结构的反应周期用相应地震波通过小波分析所得的速度脉冲周期进行归一化处理，表示结构固有周期与速度脉冲周期的关系；周期范围设定为0.10≤T/TP≤3.00（T为结构固有周期）。可以推断，所得曲线上各点的纵坐标越接近于 1，表明该结果越接近于原始地震波的结果。算例结果如图7所示。

从图7可以看出，固有周期相对于速度脉冲周期很小的结构，在高频波部分作用下将产生比脉冲波部分更接近与原始地震波的响应，但是总体准确度较差；随着延性系数μ的增加，高频波部分能保证计算精度的周期范围进一步减少；脉冲波部分在大部分结构周期范围内能保证较高的精度，尤其是在结构固有周期与脉冲周期相差不大的范围内（即T/TP≈1），但是随着延性系数的增加，能够保证精度的周期范围逐渐减小，并且向较低周期方向偏移，而且曲线大部分的纵坐标都小于1，表明出现低估位移需求的情况。

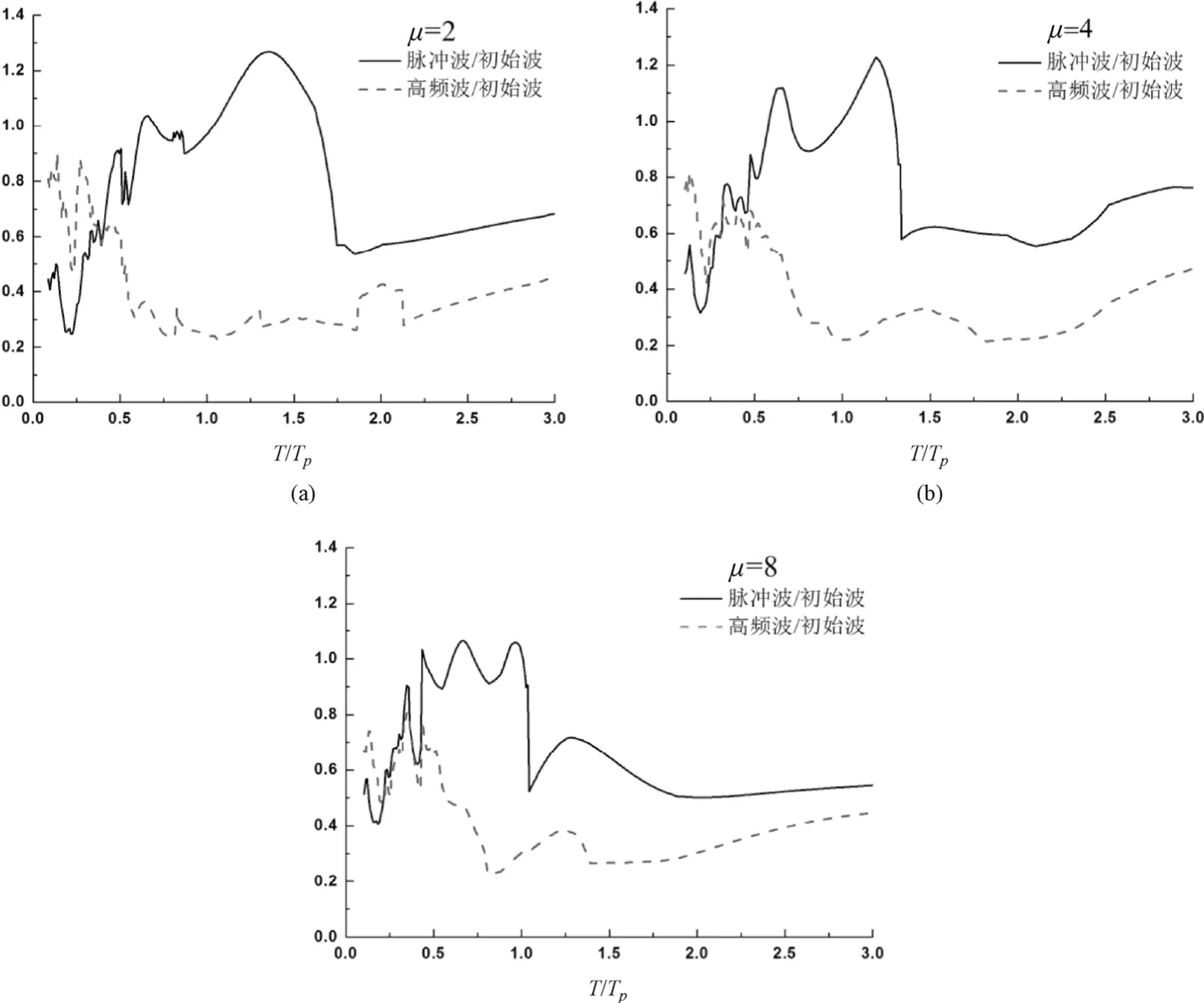
图7 地震波算例归一化等延性反应谱Fig. 7 Example of normalized constant ductility response spectra (Agraias, Imperial Valley-06, 1979)

为了直观地描述上述现象，将所得结果取平均值，列出延性系数与保证计算精度的结构固有周期范围的关系表格，由于高频波起主要作用的周期范围很小，本文只统计脉冲波部分的分析结果，如表1所示（表中精度误差小于20%，即一定固有周期范围内的结构分别在原始地震波和小波分解所得波作用下的响应的误差小于 20%）。可以看出，在用等效速度脉冲模拟近断层地震动时，一定固有周期范围内的结构能够达到精度要求，但随着延性系数的增加，能够保证计算精度的周期范围将明显减小，并且向低周期范围偏移。Alavi等（2001）指出，在0.375≤T/TP≤3的周期范围内，可以将近断层地震动用等效脉冲来表示，其结论对于线弹性体系能够满足精度要求，而对于弹塑性体系，仍将产生较大的误差。

表1 不同延性系数时保证精度的周期范围Table 1 Period range of precision guarantee with different ductility

4 结论

本文通过小波分析将近断层地震动分解为脉冲波和高频波两个部分，并分析在各自作用下单自由度弹性和非弹性体系的响应，所得结论如下：

（1）在分析近断层地震动时，高频部分不能简单地忽略，尤其是针对短周期结构和高阶模态分析。

（3）对于非弹性体系，随着延性系数的增加，仅考虑脉冲波部分或者高频波部分模拟近断层地震动都不能满足精度要求。仅用脉冲波来模拟近断层地震动进行结构分析时，所能保证计算精度的结构固有周期范围将随着延性系数的增加而缩小，并向低周期范围偏移，而且将低估结构的位移需求。

建立等效模型来模拟近断层地震动可以明确输入参数的意义，在实际工程中有很高的研究和使用价值。根据本文的研究结果，仅仅利用等效速度脉冲模型模拟近断层地震动具有一定的局限性，需要进一步研究能够模拟近断层地震动作用下非线性体系反应的等效模型。

胡进军，2009. 近断层地震动方向性效应及超剪切破裂研究. 哈尔滨：中国地震局工程力学研究所.

李明，谢礼立，杨永强等，2010. 基于反应谱的近断层地震动潜在破坏作用分析. 西南交通大学学报，45（3）：331—335.

李新乐，朱晞，2004. 近断层地震动等效速度脉冲研究. 地震学报，26（6）：634—643.

谢礼立等译，2007. 结构动力学理论以其在地震工程中的应用（第二版）. 北京：高等教育出版社.

Alavi B., Krawinkler H., 2001. Effects of near-fault ground motions on frame structures. The John A. Blume Earthquake Engineering Research Center Report. No.138.

Ghahari S. Farid, Hossein Jahankhah, M. Ali Ghanand, 2010. Study on elastic response of structures to near-fault ground motions though record decomposition. Soil Dynamics and Earthquake Engineering, 30: 536—546.

Jack W. Baker, 2007. Quantitative classification of near-fault ground motions using wavelet analysis. Bulletin of the Seismological Society America, 97: 1486—1501.

Krawinkler H., Alavi B., 1998. Development of an improved design procedure for near-fault ground motions. SMIP 98 seminar on utilization of strong motion data. Oakland CA.

Mavroeidis G.P., Dong G.., Papageorgiou A.S., 2004. Near-fault ground motions and the response of elastic and inelastic single-degree-of-freedom (SDOF) systems. Earthquake Engineering and Structural Dynamic, 33: 1023—1049.

Menun C., Fu Q., 2002. An analytical model for near-fault ground motions and the response of SDOF systems.Earthquake Spectra 2002, Feb.: 249—258.

Stewart J.P., Chiou S., Bray J., 2001. Ground motion evaluation procedures for performance-based design. Pacific Earthquake Engineering Research Center (PEER), Report No. 9.