基于UKF和信息融合的航天器自主导航方法

罗楠 许录平 张华

（西安电子科技大学电子工程学院，西安710071）

1 引言

脉冲星是一种高速、稳定自转的中子星，其辐射周期信号的长期稳定度可与铯原子钟媲美，被誉为自然界最稳定的频率基准[1]。美国科学家于1974年首次提出了利用脉冲星进行航天器自主轨道确定，开创了脉冲星导航先河[2]。将脉冲星作为航天器的导航信源有其独特的优点：脉冲星信号是自然存在的，任何时候都可以免费获取；脉冲星分布于整个天空，不同的航天器可以同时进行时间差测量；每颗脉冲星辐射轮廓都是唯一并可预测的；能为近地及星际空间的多种航天器提供导航信息。基于脉冲星辐射定时模型的导航是一种颇具潜力的航天器自主导航方法，它不仅可以脱离地基测控的支持，为近地遥感及深空探测的各种卫星提供长期稳定可靠的自主导航服务，而且能为需要多卫星数据融合的卫星系统提供星座间位置与时间的联合标定。但由于脉冲星信号弱，在目前技术条件下导航精度较低，因此组合不同类型的导航手段，用信息融合方法来完成精确、稳定的导航任务是必要的。

本文在分析星敏感器和脉冲星导航两种不同导航机制的基础上，提出了一种基于无迹卡尔曼滤波（Unscented Kalman Filter，UKF）的信息融合天文自主导航方法。结合两者在导航信息连续性和精确性上的互补优势，一方面用脉冲星提供连续不断的导航信息；另一方面利用星敏感器敏感折射星光，并通过大气对星光折射的数学模型和误差补偿技术精确敏感地平，提高这种组合导航方法的导航精度。

2 敏感地平测量模型

星光仰角是指航天器观测的恒星星光矢量方向与地心矢量方向之间的夹角，它是航天器在地心坐标系中位置矢量的函数。如图1所示，当卫星到地心与地球边缘切线方向的夹角已知，星敏感器的量测模型[2]可表示为

式中α为航天器到地心方向与到恒星方向的夹角；rE为地心坐标系中卫星位置矢量；为地心惯性坐标系中卫星到导航恒星视线方向单位矢量；vα为量测噪声，包括安装误差、地平敏感误差等。

公式 （1）表示成量测方程形式为

式中Z为量测向量；h为非线性转换方程；X（）t为卫星的状态向量；δZ为噪声向量，主要包括安装误差和地平敏感器量测误差。

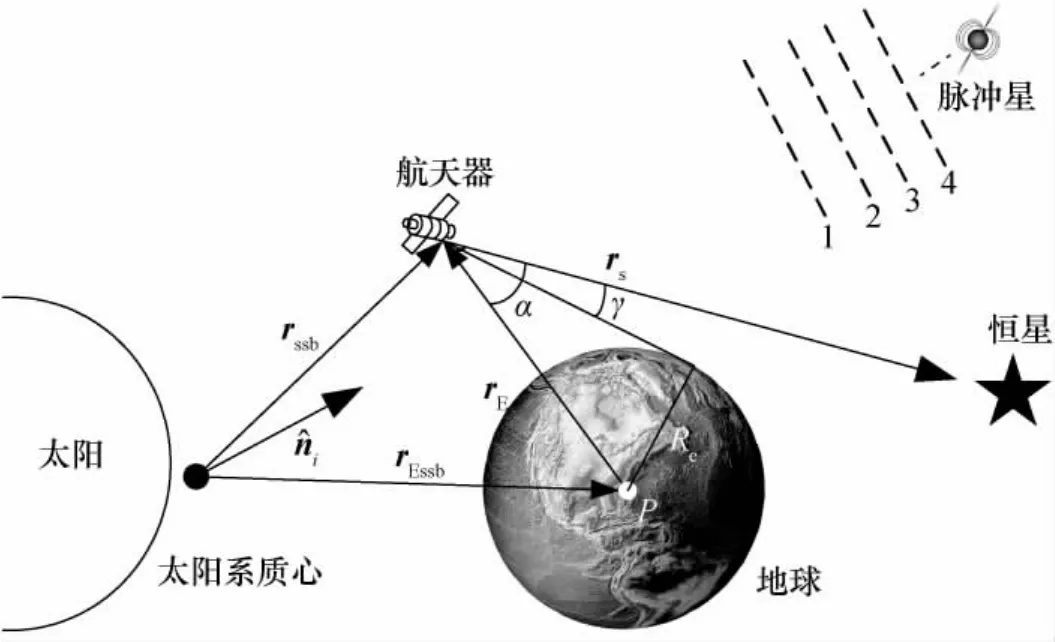
图1 星敏感器／脉冲星联合导航示意图Fig.1 Schematic diagram of integrated navigation utilizing star sensor and pulsar

3 脉冲星到达时间测量模型

脉冲星导航技术是利用探测器同时精确测量多颗特性已知的脉冲星辐射脉冲到达太阳系质心（Solar System Barycentre，SSB）和航天器的时间差，经过必要的修正测得航天器在脉冲星视线方向距SSB的距离，结合轨道动力学模型采用相应的信号处理和导航算法实现对航天器位置、速度、时间的计算和预报。采用SSB惯性坐标系作为参考架，脉冲星脉冲到达SSB相位模型[3]可表示为

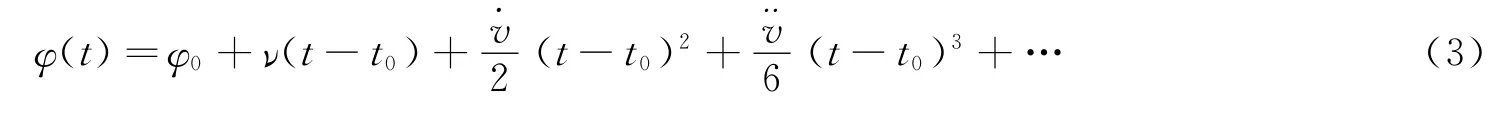
式中φ0为参考历元t0时刻的脉冲相位；ν（t）为脉冲星参考历元t时的自转频率。该模型中的参数通过对脉冲星的长期观测得到。将脉冲星辐射短期观测和累积得到的脉冲星脉冲轮廓模型，在星载原子钟保持时间（固有时）下进行比对，可以得到脉冲星到达用户星和SSB的时间差[4]。如图1所示，由于时间差是航天器位置矢量的函数，SSB坐标系下其一阶表达式可表示为

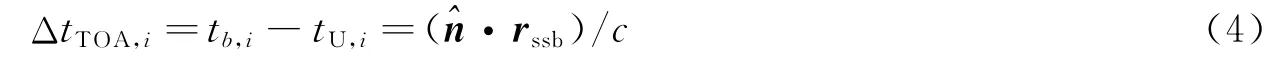
式中rssb＝rEssb＋rE；为SSB到脉冲星视线方向的矢量；tU，i为航天器测得的第i颗脉冲星辐射脉冲到达时间（Time of Arrival，TOA）；tb，i为同一脉冲在SSB处的TOA，i表示第i颗脉冲星。公式（4）的一阶方程忽略了相对论等效应对TOA测量的影响，要在工程上实现精确的脉冲星定时模型，必须将实测TOA的固有时通过各项修正转化到质心力学时（Barycentric Dynamical Time，TDB），求得TDB下的时间差：

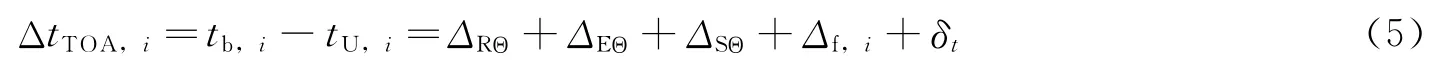
式中ΔRΘ为Roemer延迟，包括一阶多普勒延迟和视差效应；ΔEΘ为相对论效应修正，太阳系中ΔEΘ＜1ns可忽略；ΔSΘ为太阳系Shapiro延迟；Δf，i和δt分别为第i颗脉冲星色散效应误差和卫星时钟偏差。时间差测量方程可简化为

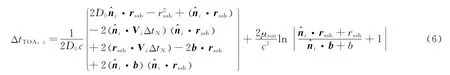
式中D0为脉冲星到SSB的距离；V为脉冲星固有运动速度；ΔtN＝tN-t0表示从脉冲星初始时刻开始到辐射第N个脉冲的时间间隔，由于D0≫VΔtN，仿真计算时VΔtN可以忽略；b表示SSB相对太阳质心的位置矢量；μsun为太阳引力常数。

式（6）用测量方程简化表示为

4 轨道动力学模型

定轨问题中轨道状态常用开普勒轨道要素或三维惯性坐标系下的位置、速度来描述。开普勒轨道六参数有5个是常量，定轨精度高，适用于特定轨道；对于具有变轨任务的卫星，使用位置、速度描述更为方便。地心坐标系下设向量X＝｛rT，vT｝T表示卫星状态，卫星运动用二体方程描述：

式中GE为地球引力常数；a为轨道摄动力，a＝anonspher＋a3body＋adrag＋aSR＋aother，其中anonspher为地球非球形引力摄动，a3body为第三体摄动，adrag为大气阻力摄动，aSR为太阳直接辐射压摄动，aother为其他摄动力。地球质心引力与各种摄动力共同决定了卫星的在轨运动。

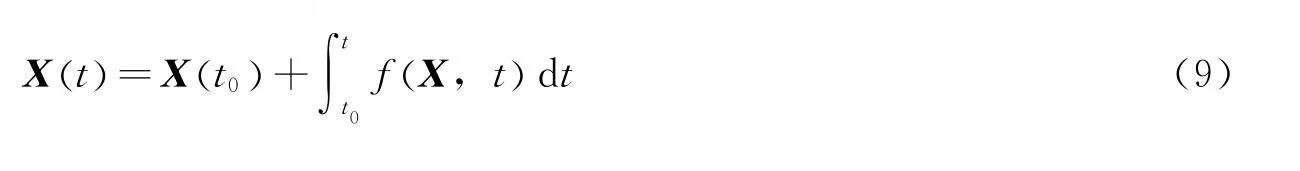
5 基于UKF的信息融合方法

定轨过程首先是对卫星受力建模，并对运动方程积分，得到预测轨道状态；然后，在量测量支持下，依赖轨道的估计采用拟合或滤波的方法进行差分改正或轨道状态改进。从以上各节分析可知，基于式（2）、式（7）的量测方程和式（9）的轨道动力学方程可构建迭代滤波对轨道状态进行改进。在系统噪声满足高斯分布，统计特性的先验知识足够的前提下，Kalman滤波是基于H2范数导出的最优线性迭代滤波方法。由于轨道改进过程的量测方程和状态方程均是非线性的，通常使用次优的扩展卡尔曼滤波（EKF），它使用泰勒级数的一阶项对观测方程和状态方程线性化。EKF有两个缺陷：对强非线性方程线性化会引入较大的误差，导致估计误差增大；线性化过程会导致假设为高斯分布的先验和后验概率的均值和方差估计错误。而无迹卡尔曼滤波（UKF）被认为是性能优于EKF的非线性滤波方法[6]，它使用一组确定的离散Sigma采样点来参数化高斯随机状态变量的均值和方差，并直接使用非线性状态方程来传播后验概率均值和方差，而不需要线性化，但UKF方法稳定性较EKF稍差。

文献[7-8]分析了X射线脉冲星导航技术在航天器行星际空间飞行中的应用，解决了相位导航存在的整周期模糊度问题。在轨道动力学模型估计航天器位置的基础上，将其真实位置和估计位置的脉冲星脉冲相位差作为反馈，使用UKF滤波来得到高精度的导航信息。本文通过分析星敏感器和脉冲星导航的工作机制，将来自这两种不同导航方式的信息源数据进行相关、组合，充分利用多个传感器提供的导航资源，合理使用它们在空间和时间上的冗余互补信息，设计了UKF联合滤波器来完成信息融合，以提高卫星自主导航的精确度。

设UKF算法的离散状态方程和测量方程为

式中xk为n维向量状态变量；f（xk-1）为状态传播函数；h（xk）为测量函数；wk和vk为非相关高斯白噪声，且分布满足wk～N（0，Qk）和vk～N（0，Rk），Qk和Rk分别为wk和vk的方差。

设UKF的算法实现过程为

4）时间更新：

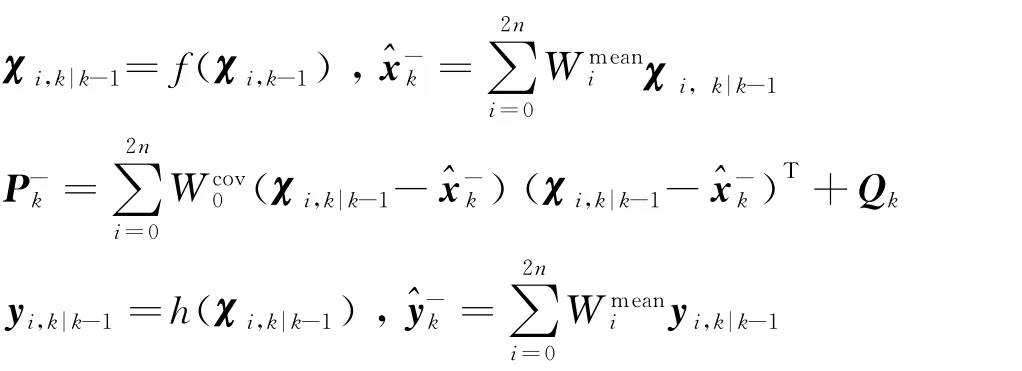
5）量测更新：

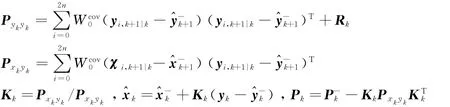
联合滤波系统中，子滤波器1基于状态方程式（9）与观测方程式（2）；子滤波器2基于状态方程式（9）与观测方程式（7）。融合滤波器将两个子滤波器的输出结果进行信息融合，完成时间更新，并将融合结果反馈到各子滤波器，作为下一级滤波的初值。鉴于UKF的稳定性较差，将一组EKF作为备份滤波器加入组合定姿系统中，用于在UKF异常时维持系统正常工作，导航信息融合方法如图2所示。

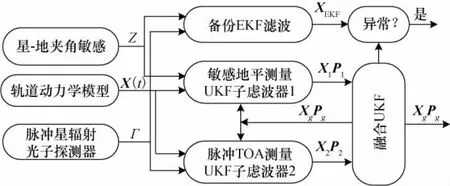
图2 信息融合方法Fig.2 Methodology of information fusion

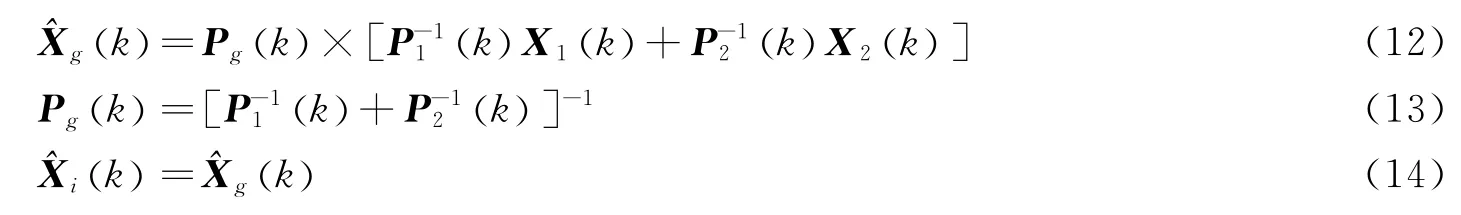
由于UKF的稳定性较EKF差，子滤波器中只反馈状态变量。卫星在轨运动由于受地球等天体遮挡影响，星敏感器观测到的导航恒星和X射线探测器探测到的脉冲星个数是不断变化的，因此两个子滤波器在运算过程中观测方程和观测噪声协方差阵也随之变化。

6 仿真分析

6.1 仿真系统

为了验证X射线脉冲星导航原理和UKF信息融合算法的可行性和有效性，利用激光光子辐射模拟脉冲星X射线光子辐射，设计了一种基于激光光量子探测的X射线脉冲星导航地面仿真系统，其硬件结构如图3所示。信号模拟计算机提取各参数库中信号模型生成脉冲星信号模拟数据和星敏感器观测数据；导航算法部分模拟星载计算机，用于X射线脉冲星信号数据和星敏感器数据处理并用于信息融合导航。时间保持单元通过现场可编程门阵列 （Field-programmable Gate Array，FPGA）综合GPS定时接收机提供的秒脉冲信号和温补晶振的时钟信号，用于标定光子发射时间；光子发射单元由激光调制与驱动、670nm半导体激光器和光学发射天线构成，用于将模拟数据转换为激光光子；光子探测单元包括接收光学天线、衰减器、670nm带通滤光器和光子探测与计数器；光学接收天线模拟X射线准直器，用于定向和噪声初步抑制，其接收的光子经过衰减器衰减后由670nm带通滤光器滤除日光中其他光谱成分，然后由时间保持单元2进行时间标定后，送至导航算法单元。

该仿真系统激光发射功率与探测到的光子数之间的关系[9]为

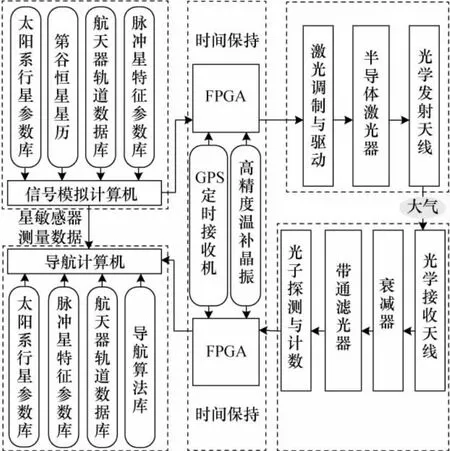
图3 仿真系统结构框图Fig.3 Frame diagram of the simulation system

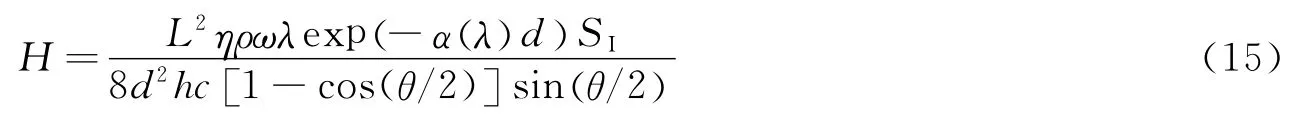
式中L为光学接收天线直径；d为激光器和探测器间距离；θ为激光光束发散角；ρ为可控衰减系数，用可调衰减器实现；ω为其他衰减；η为探测器效率；T为脉冲持续时间；h为普朗克常量；c为光速；λ为光波长；SI为闪烁因子，典型值为0.4～1.0。若设观测到的光子数为λS，背景辐射噪声为λn，激光发射功率的概率模型为[9]

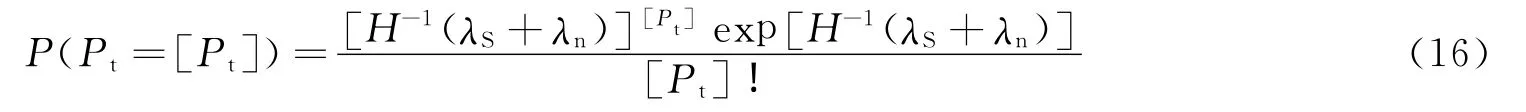
式中 [·]为取整操作；Pt为激光发射功率。仿真时系统根据模拟的轨道位置和时间确定信号的发射时间，再根据不同脉冲星空间观测信号强度和背景辐射噪声用式（16）计算激光发射功率，并对激光进行模拟调制。

6.2 仿真条件

卫星轨道动力学模型考虑地球非球形引力 （摄动函数取J2～J6项），日、月引力及大气阻力等3种摄动力，积分过程使用四阶龙格-库塔数值积分方法，积分步长设定为10s。用户星轨道初值从北美防空联合司令部提供的两行轨道根数集中选取，并使用简化常规／深空扰动的近似解析解模型[10]程序读取。用户星初始轨道误差为1.5km，并假设用户星到SSB的脉冲星辐射脉冲周期模糊数已知，卫星严格对地定向并且三轴姿态稳定。

星敏感器与红外地平仪测量1σ精度分别设为6″和0.05°，视场角5°×5°，并设观测噪声服从零均值高斯分布。恒星星历取自第谷星表数据库，仿真中滤波器从备择恒星中选取较亮的10颗作为导航星。X射线脉冲星选用B1937＋21、B1821-24、B1509-58和B0531＋21，并设脉冲星自身运动速度为零。4颗脉冲星的信号积分时间与距离测量精度关系见表1，其特征属性参数见表2，其中pf为脉冲辐射流量与平均辐射流量比，本文仿真中积分时间选500s。脉冲星TOA量测值仿真利用式（5）的简化形式加上以测距精度为方差的零均值高斯噪声完成[11]，TOA测量使用泰勒快速傅里叶变换（Taylor FFT）算法。

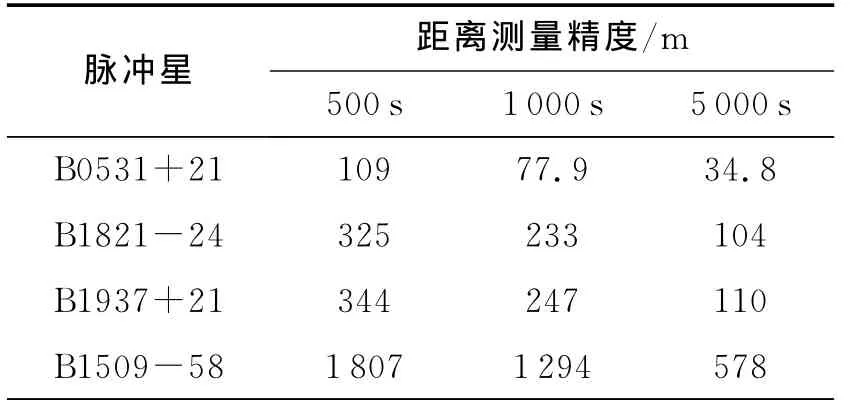
表1 脉冲星观测时间对定位精度的影响Tab.1 Pulsar range measurement accuracy over 500s，1000sand 5000sobservation time

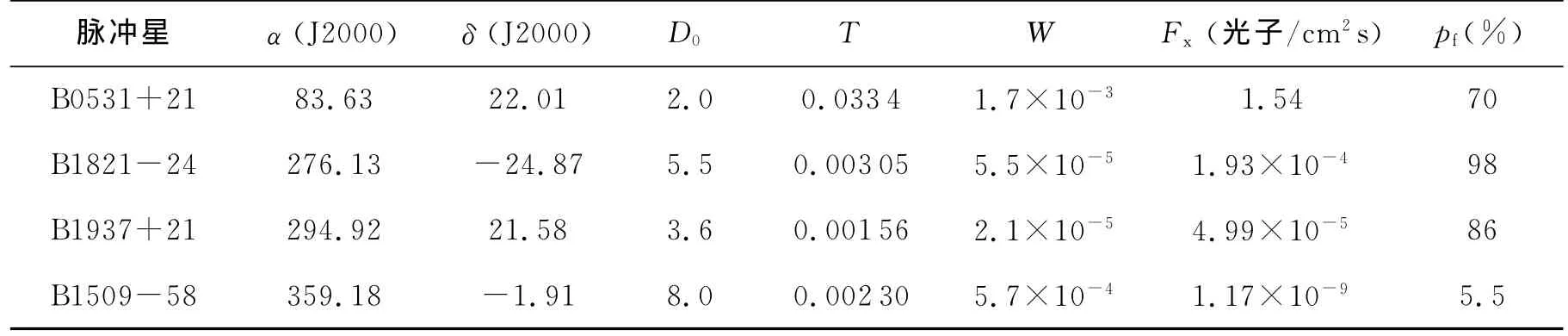
表2 用于定轨的X射线脉冲星参数Tab.2 Parameters of pulsars for orbit determination

仿真系统中半导体激光器功率5mW，中心波长670nm；光学发射天线透光率约80%，发射角（π／6）rad；光学接收天线接收面直径5cm，透光率约70%；衰减器使用两片衰减深度为10-3的可调衰减器构成，带通滤光片中心波长（670±10）nm，峰值透过率55%；光子探测与计数器有效光敏面直径20μm，暗计数50个／s，670nm波长光子探测效率为10%，光学发射天线与光学接收天线相距3m，采样间隔（1／1024）s。以脉冲星B1937＋21为例做信号累积试验，累积500s得到累积脉冲轮廓与标准轮廓的比较如图4所示。计算二者相关系数为0.996，可以说明该系统可以较好地模拟出脉冲星辐射信号。

6.3 仿真结果

选取LEO卫星MEGSAT-1（卫星号26546U）做定轨试验。图5是一段分别使用星敏感器、脉冲星和信息融合方法导航，滤波周期为500s的仿真结果。从图5的仿真结果可以看出，滤波收敛后，融合方法收敛速度更快，导航精度整体优于单独使用脉冲星或星敏感器方法的精度。

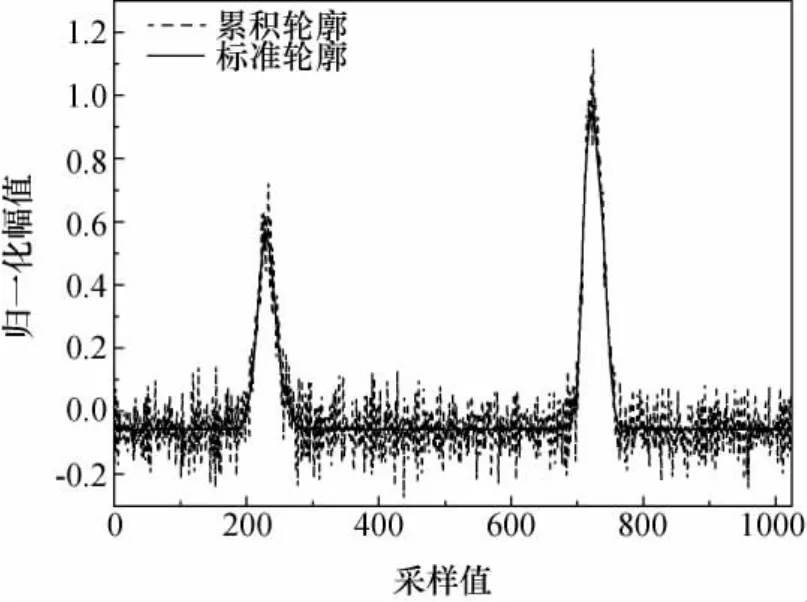
图4 脉冲星累积轮廓与标准轮廓Fig.4 Standard and accumulated profiles of pulsar

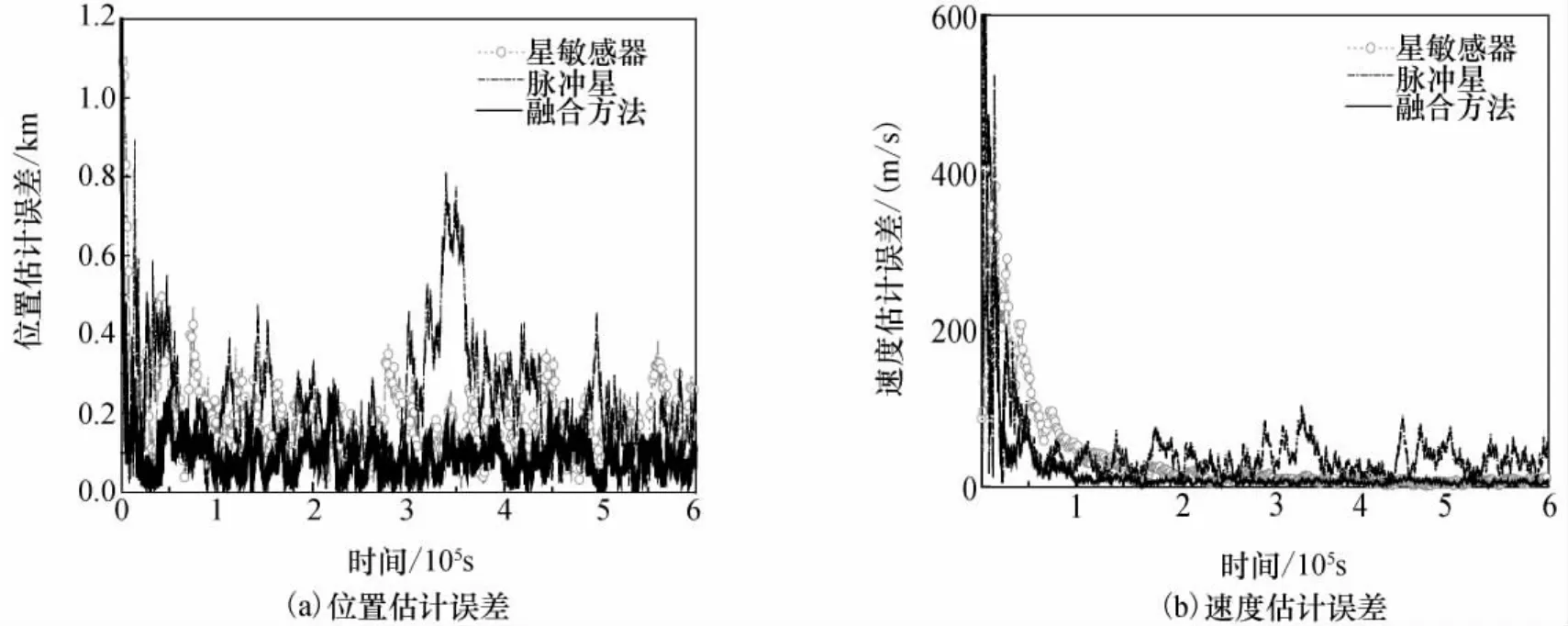
图5 星敏感器、脉冲星及融合方法定轨位置和速度误差Fig.5 Position and velocity errors of star-sensor，pulsars and information fusion method

在相同仿真条件下，表3给出了使用EKF和UKF方法进行信息融合时，3种导航方法位置、速度的估计误差结果。由表3可知，基于UKF的信息融合方法位置估计精度比单独使用脉冲星和星敏感器的导航方法分别提高了52.7%和43.6%，速度估计精度分别提高了82.2%和70.5%。

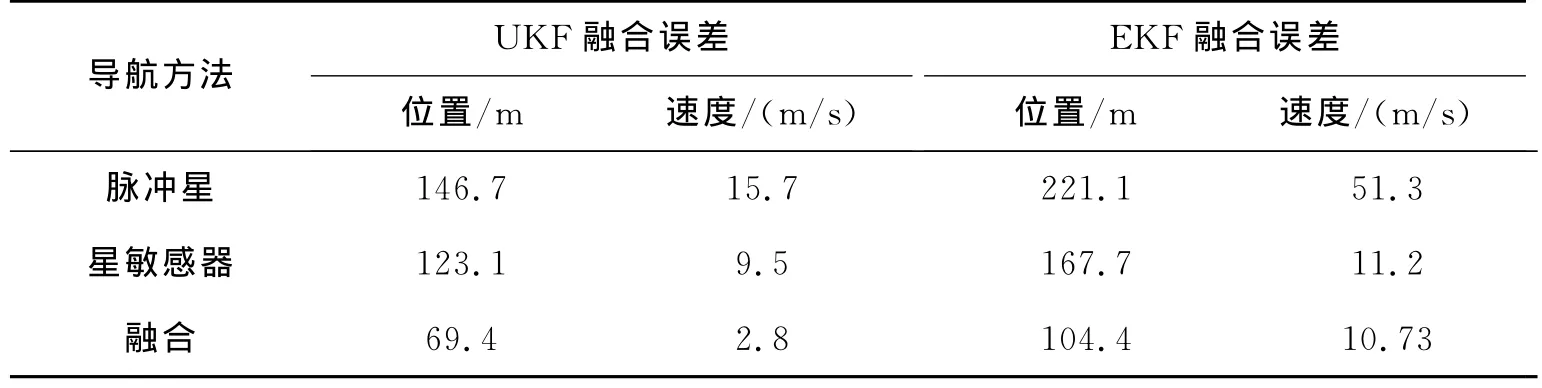
表3 脉冲星、星敏感器、融合方法进行位置、速度估计的误差对照Tab.3 Estimation errors of position and velocity using pulsars，star-sensor and information fusion method respectively

从图5和表3给出的仿真结果可得出结论：1）脉冲星导航由于脉冲星辐射信号弱的限制，估计精度要略低于星敏感器；2）结合脉冲星和星敏感器的融合导航方法估计精度显然高于单一导航方法，尤其是使用UKF时，导航误差更小，大幅度地提高了导航精度。

图6给出了相同的仿真条件下用EKF和UKF进行信息融合时，位置和速度估计误差的比较。从图中可以看出UKF融合方法能得到比EKF融合方法更好的性能。结合表3给出的估计误差结果，从图6（a）和（b）中的曲线对比可以发现：1）UKF方法相比于EKF来说，收敛得更快，收敛后估计精度更高；2）基于EKF的信息融合方法位置和速度估计精度虽然比基于UKF的信息融合方法差，但仍然优于仅使用星敏感器或脉冲星的导航方法。

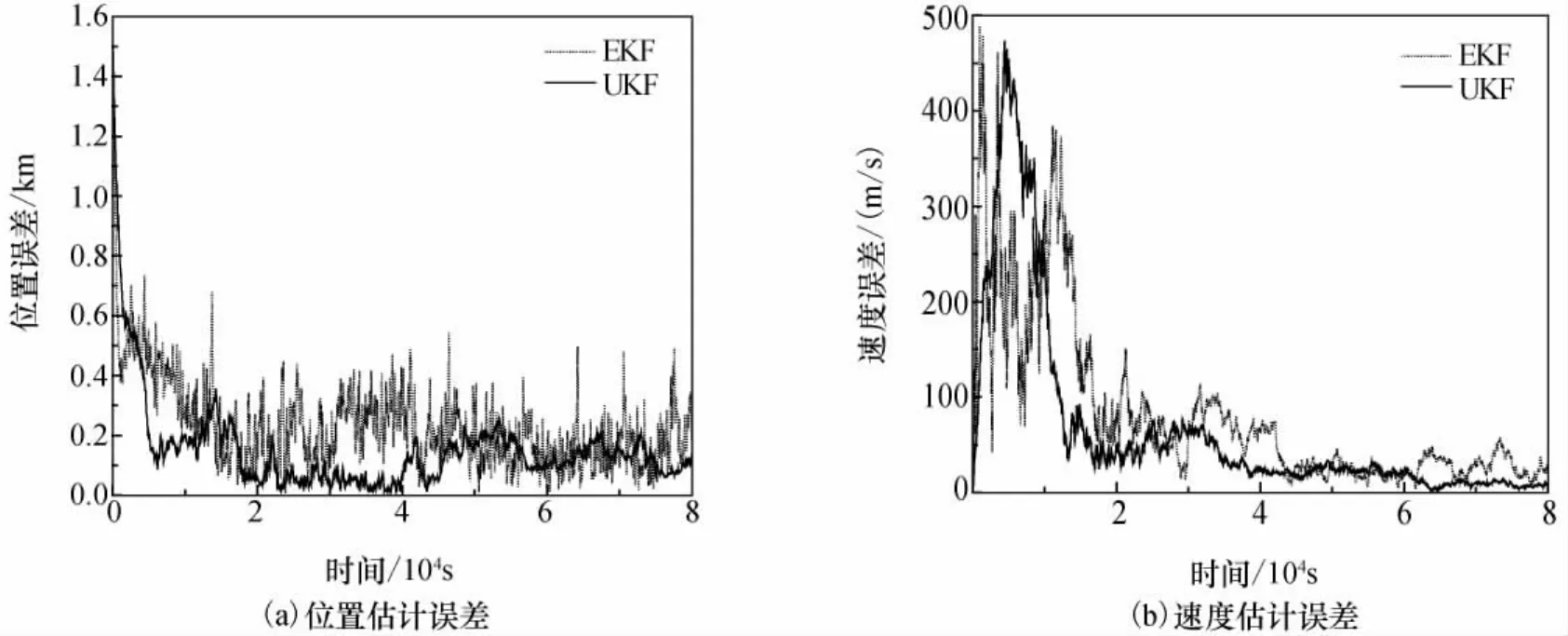
图6 UKF、EKF信息融合方法误差Fig.6 Error of UKF and EKF information fusion

仿真试验结果表明，无论使用那种滤波器，融合方法均提高了导航精度，是完成精确导航任务的更佳选择。但由于UKF必须保证迭代过程中Pk-1的正定性，其滤波稳定性却不如EKF，导航系统可使用UKF作为主滤波器，EKF作为副滤波器，以提高信息融合系统的可靠性。

7 结束语

基于UKF的信息融合方法，有效地组合了基于星敏感器和基于脉冲星两种不同的导航技术，性能明显优于仅使用星敏感器或脉冲星的导航方法，且优于EKF融合方法。设计了利用激光光子模拟脉冲星X射线光子的半实物仿真系统，利用该系统验证了融合方法的有效性。信息融合导航方法具有完全自主性，可作为星载导航系统的备份，提高系统可靠性并可集成于星载处理器，不仅能用于地球轨道卫星导航，还能为深空探测和太阳系空间航天器提供导航定位服务。

[1]JOSEPH H，TAYLOR J H.Millisecond pulsars：nature′s most stable clocks [J].Proceedings of the IEEE，1991，79（7）：1054-1062.

[2]李建勋，柯熙政.基于脉冲星定时模型的自主导航定位方法 [J].中国科学（G辑：物理学 力学 天文学），2009，39 （2）：311-317.LI JIANXUN，KE XIZHENG.Study on autonomous navigation based on pulsar timing model[J].Science in China（Series G：Physics，Mechanics and Astronomy），2009，39（2）：311-317.

[3]DOWNS G S.Interplanetary navigation using pulsating radio sources[R].NASA，N74-34150，1974：1-2.

[4]帅平，陈忠贵.关于X射线脉冲星导航的轨道力学问题 [J].中国科学（E辑：技术科学），2009，29（3）：556-561.SHUAI PING，CHEN ZHONGGUI.Several problems of orbital mechanics about X-ray pulsar navigation[J].Science in China （Series E：Technological Sciences），2009，29（3）：556-561.

[5]SHEIKH S I，PINES D J.Recursive estimation of spacecraft position and velocity using X-ray pulsar time of arrival measurement[J].Navigation，Journal of the Institute of Navigation，2006，53（3）：149-166.

[6]WAN E A，VAN DER MERWE R.The unscented Kalman filter for nonlinear estimation [C].Adaptive Systems for Signal Processing，Communications，and Control Symposium 2000，AS-SPCC，the IEEE 2000，2000：153-158.

[7]杨博，郭星灿，杨勇.X射线脉冲星导航在行星际轨道上的应用 [J].北京航空航天大学学报，2009，35（11）：1384-1387.YANG BO，GUO XINGCAN，YANG YONG.Use of X-ray pulsar-based navigation method on interplanetary trajectory [J].Journal of Beijing University of Aeronautics and Astronautics，2009，35（11）：1384-1387.

[8]YANG BO，GUO XINGCAN，YANG YONG.The use of X-ray pulsar-based navigation method for interplanetary flight[C].International Symposium on Photoelectronic Detection and Imaging 2009：Terahertz and high energy radiation detection technologies and applications，Beijing，2009：17-19.

[9]张华，许录平.基于光量子探测的XPNAV半物理仿真及建模 [J].光电子·激光，2011，22（6）：905-910.ZHANG HUA，XU LUPING.Hardware in-the-loop simulation and mode ling for XPNAV based on light quantum detection [J].Journal of Optoelectronics·Laser，2011，22 （6）：905-910.

[10]HOOTS F R，ROEHRICH R L.Spacetrack report No.3models for propagation of NORAD element sets[R].Department of Defense，Defense Documentation Center，1980.

[11]SHEIKH S I，PINES D J.Recursive estimation of spacecraft position using X-ray pulsar time of arrival measurements[C].ION 61st Annual Meeting，Cambridge，MA，2005：27-29.