河道洪水传播时间的预报方法

杨瑞恒

（邯郸水文水资源勘测局，河北邯郸056001）

河道水文预报最关键的预报要素有洪峰流量、洪峰出现时间和洪量。根据上游断面来水过程，预报下游河道洪峰流量和峰现时间对于防洪减灾具有重要意义。北方地区河道多为季节性河流，河道上游流量的大小、断流时间的长短、区间河槽干旱程度及河槽下垫面变化等都会对洪水传播时间产生一定影响。本文拟以清漳河刘家庄水文站和匡门口水文站区间为例，采取不同的方法，探讨河道洪水传播时间的规律。

1 区域基本情况

清漳河发源于山西省，于涉县辽城乡进入河北境内，在涉县合漳村与浊漳河汇合为漳河。清漳河为山区性河流，河槽宽浅，河道蜿蜒曲折，洪水暴涨暴落，河道纵坡27%，糙率0.030～0.035。自20世纪80年代以后，随着水资源开发利用程度的提高及下垫面变化等影响，河道时有断流现象发生。

刘家庄水文站集水面积5001km2，历史最大流量5650m3/s，发生在1963年；匡门口水文站位于刘家庄下游43km处，与刘家庄站区间集水面积1221km2，历史最大流量5250m3/s，发生在1996年。2个水文站均为国家基本站，有50多年的水文系列观测资料。在匡门口水文站上游约500m处有西达电站渠截取清漳河水发电，其水量很小，尤其在大洪水时所占比重甚微，对区间洪水传播时间不构成影响。

2 流量与传播时间关系模式的确定

河道洪水传播时间与洪水的平均速度和计算河段长度有关。为了分析传播时间与流量关系Q～T的曲线模式，首先研究单位河长的Q～t关系形式，即假定河长为1m时的流量与传播时间的关系曲线。河道水量平均推进1m需要的时间为：

式中 t为时间（s）；v为平均速度（m/s）。

根据匡门口和刘家庄水文站1996年8月份洪水的实测流量成果表，查得各个测次的流量Q与断面平均流速v，计算t值。根据不同级别的流量与单位河长传播时间绘制Q～t关系图，见图1、图2。

图1 刘家庄断面Q～t关系

图2 匡门口断面Q～t关系

从图1、图2中可以看出，涨水期传播时间数据落在图的左侧，比落水期传播时间系统偏小。灾害性洪水预报工作主要发生在涨水期，本分析以涨水期数据作为依据。

通过绘制单位河长流量与传播时间的关系，说明：①洪水传播时间与流量级别成反比，对于一定的河段，流量越大流速越快，传播时间越短；②同级别流量对应的流速涨水期比落水期偏大，传播时间短；③流量级别较小时流速随流量的变化比较明显，流量与传播时间呈明显的反比关系；而当流量级别较大时，在一定流量范围内（如这2个站流量在2000～5000m3/s时）河道平均流速变化不太显著，具有相对稳定性。究其原因：①随着水面的开阔，水位的小幅度变化，就会形成流量的显著增大，也就是说流量增大而水力半径无明显变化；②糙率维持在一定范围基本稳定；③高水时水面比降接近河底水力坡度亦相对稳定。根据曼宁公式和谢才公式：

式中 v为平均速度；R为水力半径；I为水面比降；n为河道糙率。

在R、n、I三者基本稳定时，v也会相对稳定。

图1、图2中的河道流量与传播时间关系模式，是基于1m的单位河长的模型，对于一定距离的河段，假定为数个单位河长的组合，这样取若干个这种形式的单位河长Q～t关系模式按平均速度计算的组合，即为一定距离河长的Q～T关系线。这个关系图给出了流量与传播时间的基本关系模式，无论单位河长，还是一段河长其关系的基本形式是相同的。

3 根据单位河长的Q～t关系推求河段Q～T关系

在单位河长Q～t关系中，t为流速的倒数。根据这个关系曲线，查出不同流量级别的断面平均流速。对于一个河段，选择几个有代表性的断面，计算出不同流量级别的平均流速，推求河段的传播时间，建立该河段流量与传播时间关系。

图3 刘家庄匡门口洪峰流量相关图

刘家庄至匡门口站区间河段只有43km，河道均处于涉县境内，2个站有一定的代表性，在此以2个站的流速均值推求河段的Q～T关系。

因洪峰流量在传播过程中存在河道渗漏损失，也有坦化现象。在洪水传播过程中，洪峰流量会逐渐减小，不能用2站相同流量对应的流速直接求均值，需推求下游匡门口断面的相应流量。根据历史资料，建立刘家庄与匡门口2站洪峰流量关系，见图3。经分析，洪峰衰减系数a值为0.66。匡门口断面的流速应当采用上游刘家庄站流量传播至这一断面的相应流量aQ刘所对应流量的相应流速。

在建立区间Q～T关系时，首先根据图1中刘家庄站Q～t关系线，摘录不同量级的流量对应单位河长传播时间t1，并计算其平均流速（v1=1/t1），由图2计算出匡门口站相应流量的单位河长传播时间t2和速度v2，将这2个代表断面平均速度的均值作为河段平均速度v，计算出不同级别流量在河段的传播时间。

当然，这个流量与传播时间关系是理想状态下的关系，是传播时间的下限临界值，采用Q～T0表示，见图4。实际中，河道除存在稳定下渗外，前期河道干涸程度，流量变大水位升高存在的填洼初损等，会造成传播时间延长。

4 分析流量与传播时间的关系

4.1 根据历史多次洪水资料建立Q～T关系线

根据历史上2站对应的洪峰流量及发生时间，以2站对应峰顶出现时间差作为相应洪水的传播时间。摘录了1963年以来的2站相应洪峰流量和洪水传播时间。据此，以刘家庄至匡门口断面的传播时间T为横坐标，以上游断面刘家庄水文站的洪峰流量Q刘为纵坐标点绘流量与传播时间关系。由图5可以看出，Q～T关系点据比较分散，尤其流量小于500m3/s时，同一量级的流量，洪水传播时间最大的达到12h，小者只有3～4h，两者相差4倍，说明仅用洪峰流量与传播时间建立单一关系，其预报精度会较低，需对影响传播时间的因素进一步分析。为此，参照所有点据沿左侧和右侧边缘画出两条外包线，即下包线Q～T1和上包线Q～T2，这样同一量级的洪峰流量对应T1和T2两个传播时间，其差值为△T=T2-T1。

图4 Q～T0关系图

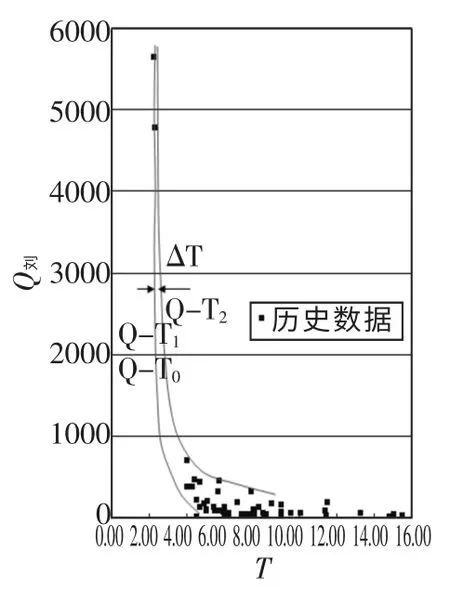
图5 Q刘～T关系图

4.2 上包线、下包线及两条曲线之间差值△T的含义

通常流量越大断面平均速度越高，传播时间亦越短，洪水传播时间与流量的大小成反比，但同一个量级的洪水，传播时间存在较大差异，流量较小时差异更加明显。其影响因素主要有河道初损、河道渗漏、河道植被变化、人类活动影响等。河道初损与前期是否过水、断流时间长短、河道干旱程度有关。

图5中下包线Q～T1表示在已发生的历次洪水传播中，不同量级洪峰流量对应的最短传播时间，是传播时间的下限。下包线Q～T1与临界曲线Q～T0曲线重合，视为除河道稳渗、洪水传播过程中坦化自然变化，初损和其他影响因素不明显时的理想传播时间；Q～T2关系线表示历次洪水传播中，不同量级洪峰流量对应的最长传播时间，是传播时间的上限，是最不利情况下洪水传播所需时间，如河道前期长时间断流、河道干涸；而2个区间的间距△T为相应流量级别洪水传播时间的最大滞后值。

传播时间主要受初损影响时可理解为：初损△W=α△TQ。初损值△W在一定范围时，流量越大，单位时间来水量越多，弥补河道初损需要时间越短，反之流量较小时弥补河道初损需要时间就会长一些，因此Q量级越小两线的间距△T值越大，Q量级越大两线间距△T值就会越小，从低水至高水两条外包线间距越来越小。为此在进行洪水传播时间预报时，根据前期影响情况，将影响级别分为轻、中、重3个级别，参照上包线、下包线和中线进行传播时间预报。河道前期流量对传播时间的影响参数采用式（3）计算：

式中 β为前期影响参数，取0～1；β≥0.4时，可参照下包线Q～T1，0.4＞β≥0.2可参照中线；0.2＞βa≥0时可参照上包线Q～T2；Q同为下游预报断面的同时流量，即进行预报时下游匡门口断面的流量；Q为上断面刘家庄洪峰流量；根据Q刘～T关系，查得刘家庄站不同流量级别传播时间，见表1。

表1 刘家庄至匡门口区间不同级别洪水传播时间

5 误差分析

为了检验刘家庄至匡门口区间Q～T关系，对有资料以来几次较大的洪水进行检验。

通过对预报传播时间与实测洪峰传播时间对照分析。在最大的5次洪峰中4次误差在0.3h以内，相对误差在±10.0%以内的点据占80%，尤其在流量大于700m3/s的高水部分误差更小。历次洪水预报传播时间误差分析见表2。

表2 历次洪水预报传播时间误差分析

6 结语

受河道前期水量影响，河道洪水流量与传播时间的关系Q～T为一个由下而向上逐渐收缩的带状区域。在低水部分流量变化对传播时间的影响显著，随着流量的增大，到一定程度时传播时间相对稳定，而且低水部分河道前期水量（或干旱程度）对传播时间影响十分明显。

通过建立Q～T关系的上包线和下包线，确定了洪水传播时间的取值范围，能够有效地提高洪水传播时间的预报精度。

利用临界曲线方法，可解决缺乏历史监测资料的河道洪水传播时间预报问题。

［1］王春泽，胡军波，刘彦华，等.时变参数法在洪水预报中应用［J］.水文，2010（5）.

［2］长江水利委员会.水文预报方法［M］.北京：水利电力出版社，1993.