结构振动的负刚度控制

汪志昊，杨亚彬

(华北水利水电学院，河南 郑州450011)

自Yao［1］1972年系统地提出结构振动控制的概念以来，结构振动控制在过去的近40年里得到了长足的发展.结构主动与半主动振动控制技术在结构振动控制领域占有重要地位，相应控制力的特性也是一个关注已久的问题.

欧进萍［2］首次系统研究了建筑结构层间主动控制力的特征，取得了层间控制力主要体现为阻尼力的重大发现. 在此基础上，Li 等［3］深入研究了建筑结构隔震系统的隔震层主动控制力特征，解释了基于智能阻尼器的半主动控制完全可以达到主动控制效果的原因.张春巍等［4］研究了建筑结构主动质量阻尼器的主动控制力特性，结果发现主动控制力只有50% 的情况下体现为阻尼力，从而阐明了基于变阻尼系统的调谐质量阻尼器难以达到主动控制的效果.汪志昊与陈政清［5］研究了隔震桥梁主动控制装置控制力的特性，结果发现主动控制力主要表现为阻尼力，因此可以用半主动变阻尼阻尼器，甚至用被动粘滞阻尼器替代主动控制器，这也在一定程度上解释了已有研究者的一个困惑，即隔震桥梁的半主动控制或主动控制相对最优被动控制在很多情况下难以体现预期的显著优越性.

此外，在结构振动主动与半主动控制的研究中发现了主动控制力的负刚度现象［6－12］. Iemura 与Pradono［7］最早明确提出了结构振动的负刚度控制策略.笔者系统回顾与研究了结构振动负刚度控制的来源、作用及实现方式，以便为负刚度控制的实际工程应用打下基础.

1 阻尼器出力与位移关系

图1给出了3 种典型的阻尼器力与位移滞回曲线，3 种滞回环的面积相等，分别对应零刚度、正刚度与负刚度3 种情况.

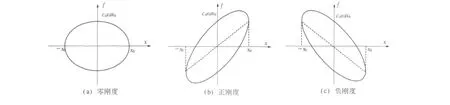
图1 具有不同刚度特性的阻尼器力－位移滞回曲线

图1中，刚度由虚线斜率表征. 所谓负刚度控制，即控制装置的出力与位移存在一个负斜率.理想的粘滞阻尼器在较低的振动频率(3 Hz 以内)工作时，一般认为其具有零刚度.正刚度的典型代表是粘弹性阻尼器，而内刚度为负的被动阻尼器较少.

2 负刚度控制的作用

对结构振动被动控制的实际阻尼器而言，不可避免地存在一定的内刚度，一般认为内刚度对阻尼器的耗能起负面作用，因为刚度会使阻尼器两端的实际相对位移减小. 下面分别以安装阻尼器的单自由度结构与拉索减振系统为例分析负刚度控制的作用，并着重考察负刚度控制对结构模态阻尼比的影响.

2.1 单自由度振动系统

对图2所示的安装阻尼器的单自由度结构振动系统而言，忽略结构固有阻尼时的自由振动运动方程为

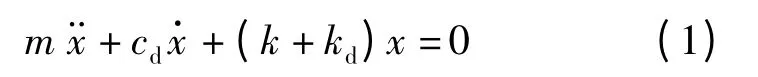
式中:m，k 分别为结构的质量与刚度;cd，kd分别为阻尼器的线性粘滞阻尼系数与刚度系数.

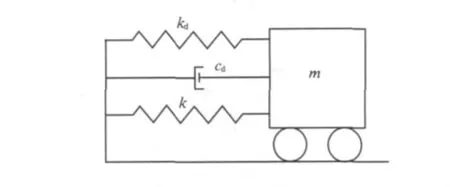
图2 单自由度振动系统

据此得到结构的模态阻尼比表达式为

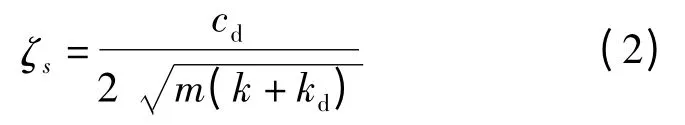
式(2)表明，在m，k，cd一定的前提下，kd越小，阻尼器对系统附加模态阻尼比的提高就越大. 如果能够使kd＜0，阻尼比的提高就会更加明显，此时的负刚度直观上体现为结构振动频率的降低.

2.2 拉索减振系统

随着斜拉桥的跨度逐渐增大，由于斜拉索的柔性、相对小的质量及较低的结构阻尼，拉索极易发生大幅的风振、风雨振和参数振动等.外置机械阻尼措施是一种最为常见，也较为有效的拉索减振方式.考虑阻尼器内刚度的影响，安装线性粘滞阻尼器后斜拉索的模态阻尼比可以表示为［13］

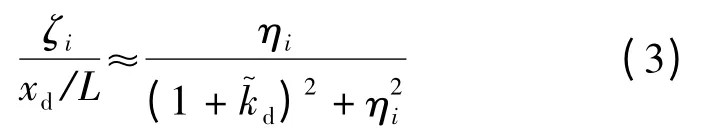
式中:xd为阻尼器安装位置与邻近的拉索锚固端之间距离;L 为拉索的长度;ηi与分别为无量纲的阻尼参数与阻尼器内刚度，

式中:T 为拉索的索力;ωi为拉索的第i 阶模态频率;cd为线性粘滞阻尼器的阻尼系数. 不难看出，阻尼器的正刚度会降低拉索可以实现的最大模态阻尼比，这也正是内刚度几乎为零的液体粘滞阻尼器在拉索减振中应用较为广泛的原因. 若采用最优被动粘滞阻尼设计，即取ηi=1，根据式(3)就可以得到图3所示的拉索约化模态阻尼比ζi/(xd/L)随无量纲刚度的变化关系.从图3可以清晰地看出，在一定范围内的负刚度可以显著提高拉索所能达到的最大模态阻尼比，特别地当=－1，拉索的模态阻尼比达到最大值，且为零刚度对应值的2 倍.

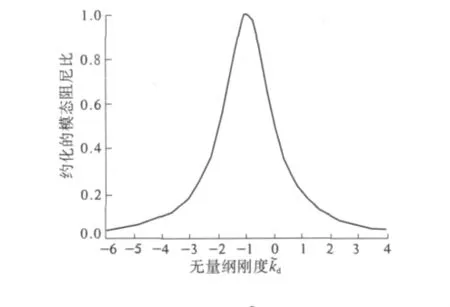
图3 ζi/(xd/L)随的变化关系

3 负刚度控制实现系统的分析

由图3联想到开发内刚度为负的阻尼器，从而提高结构的减振效果. 实际的被动阻尼器刚度均体现出正刚度或零刚度，一般来说只有主动控制装置才能实现控制力的负刚度特性.最近的研究表明，依托主动控制的半主动控制系统也具有实现负刚度控制的能力［6－12］.

3.1 主动变阻尼控制系统

Iemura 与Pradono［6］最先基于主动变阻尼控制系统发现了控制力的负刚度特性，并系统地提出了结构振动的负刚度控制算法，结合开发的主动变阻尼装置试验测试，得到了主动变阻尼装置的力学模型

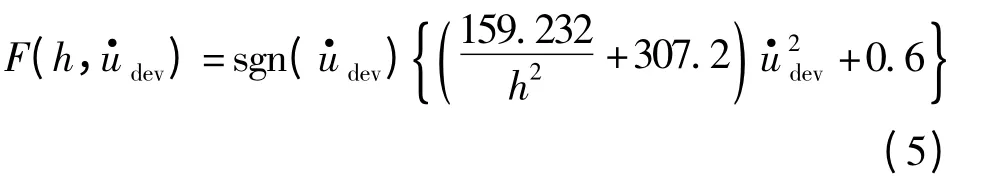
Iemura 与Pradono［7］提出的负刚度控制算法为

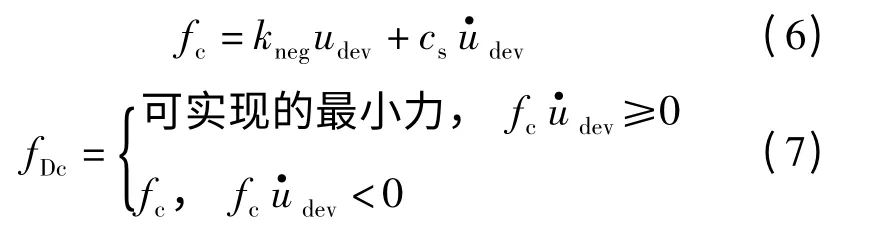
式中:kneg与cs分别为预先确定的负刚度与阻尼系数;fc与fDc分别为理论计算的主动控制力与主动变阻尼装置可以实现的阻尼力;udev与分别为阻尼器的相对位移与速度.该控制策略的主要思想是:当主动控制力与阻尼器的速度反向，即主动控制力表现为阻尼力时，通过式(5)反算阻尼器的开孔率，使此时的主动变阻尼装置产生与主动控制力接近的阻尼力;当主动控制力与阻尼器的速度同向时，将开孔率调节到最大，即调节此时的阻尼力至最小.

图4给出了按照这种控制策略，对一个钢框架结构减震试验测试得到的阻尼器出力与位移的关系曲线.

图4 主动变阻尼装置体现的负刚度特性

从图4中可以看出，主动变阻尼装置体现出预期的负刚度.采用这一方法，Iemura 等先后研究了斜拉桥的Benchmark 控制问题［6］与日本一座斜拉桥［7］的半主动减震控制，均取得了较好的减震效果.从上面的分析可以看出，负刚度控制属于分散控制，即只需要局部的阻尼器相对振动信息反馈控制主动变阻尼装置的开孔率，从而简化了结构振动控制系统，体现出很强的实用性.

3.2 普通MR 阻尼器控制系统

Iemura 等［8－9］还首次研究了通过调节磁流变(MR)阻尼器的输入电压实现结构振动的负刚度控制，并先后用于智能隔震建筑结构与高架桥Benchmark 问题的减震控制仿真分析.Iemura 等［9］提出的MR 阻尼器输入电压切换规则为

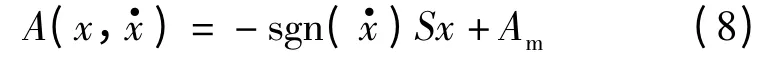
图5进一步给出了MR 阻尼器输入电压的示意图.

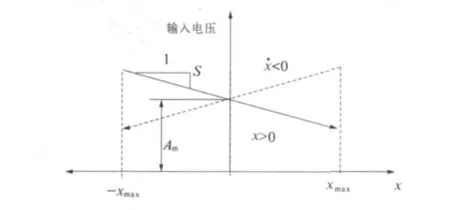
图5 MR 阻尼器的输入电压控制示意图

结合式(8)与图5可以看出:当阻尼器从最大负位移逐渐向最大正位移运动，速度为正，此时MR 阻尼器输入电压逐渐线性降低;当阻尼器从最大正位移逐渐向最大负位移运动，速度为负，此时MR 阻尼器输入电压也是逐渐线性降低;MR 阻尼器的控制电压仅需阻尼器的速度方向与位移进行反馈控制.图6给出了试验得到的MR 阻尼器力与位移的关系曲线. 由图可知，式(8)控制算法下的MR 阻尼器体现出了明显的负刚度控制特性.

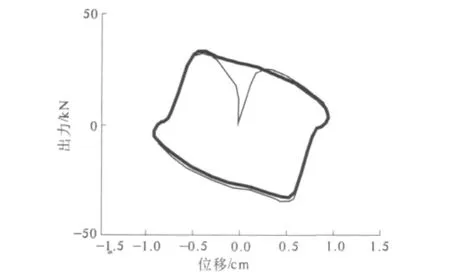
图6 MR 阻尼器出力与位移的关系

此外，Li 等［10］、Ou 与Li［11］在研究斜拉索的半主动振动控制时，也发现了MR 阻尼器的负刚度现象.图7给出了文献［10］斜拉索风致振动控制的MR 阻尼器力与位移关系的典型曲线及MR 阻尼器跟踪主动控制力的情况.

3.3 自供电MR 阻尼器控制系统

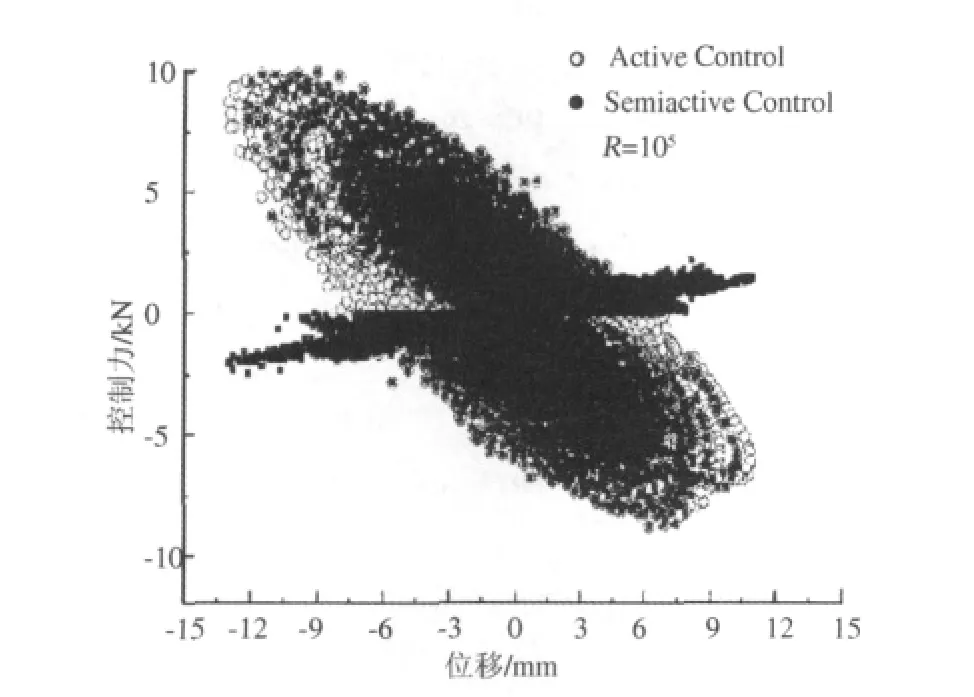
图7 主动、半主动控制力与位移的关系

为了解决MR 阻尼器对外部电源的依赖，陈政清与汪志昊［12，14］基于结构振动能量回收原理研制了具有自供电特性的MR 阻尼器系统，其由能量回收电机与只需较小能量供给的MR 阻尼器集成. 基于自供电MR 阻尼器被动控制的模型斜拉索减振试验平台开展的一系列减振试验结果表明［12］:自供电MR 阻尼器对模型斜拉索(长21.6 m)的前5 阶模态振动均具有较好的控制效果，既能够大幅提高拉索的模态阻尼比，又不会造成MR 阻尼器的嵌固，使得减振效果与拉索的振动幅值水平几乎无关，而外供电MR 阻尼器被动控制只能在拉索振动幅值较大时，才有较好的减振效果. 进一步分析表明，自供电MR 阻尼器对拉索优越的减振效果主要归功于减振系统同时具有的粘滞阻尼与负刚度控制特性. 图8给出了典型工况下的自供电MR 阻尼器力－位移关系曲线.由图8可知，自供电MR 阻尼器从第2 阶模态开始体现出阻尼力的负刚度特性，且模态阶数越高，负刚度特性越显著.

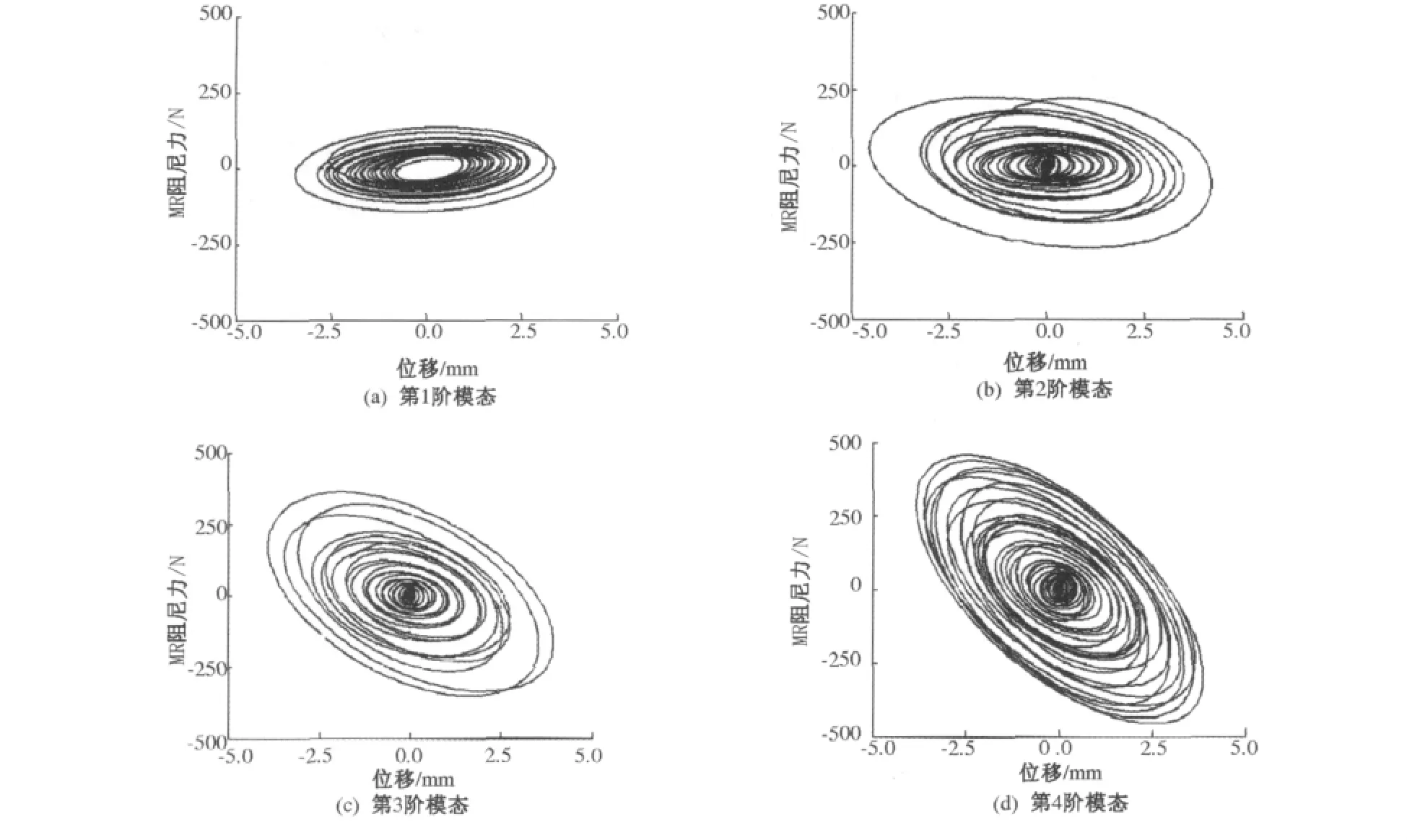
图8 拉索减振系统中自供电MR 阻尼器出力与位移的关系

4 结 语

目前，基于直接负刚度控制的结构智能减振系统的研究还较少，下一步应加大研究使得负刚度控制能够直接应用于实际工程，从而在保证减振效果的同时简化现有的主动与半主动控制系统.

［1］Yao J T P.Concept of structural control［J］.ASCE Journal of the Structural Division，1972，98:1113－1119.

［2］欧进萍. 结构振动控制—主动、半主动和智能控制［M］.北京:科学出版社，2003.

［3］Li H，Ou J P.A design approach for semi-active and smart base-isolated buildings［J］. Structural Control and Health Monitoring，2006，13:660－681.

［4］张春巍，欧进萍. 结构振动AMD 控制系统主动控制力特征指标与分析［J］.工程力学，2007，24(5):1－9.

［5］汪志昊，陈政清.隔震桥梁地震反应的最优主动控制力特性研究［J］.振动工程学报，2011，24(2):175－180.

［6］Iemura H，Pradono M H. Application of pseudo negative stiffness control to the benchmark cable-stayed bridges［J］.Journal of Structural Control，2003，10(3):187－203.

［7］Iemura H，Pradono M H. Simple algorithm for semi-active seismic response control of cable-stayed bridges［J］.Earthquake Engineering and Structural Dynamics，2005，34(4):10－25.

［8］Iemura H，Igarashi A，Pradono M H，et al. Negative stiffness friction damping for seismically isolated structures［J］.Structural Control and Health Monitoring，2006，13(2－3):775－791.

［9］Pradono M H，Iemura H，Igarashi A，et al. Passively controlled MR damper in the benchmark structural control problem for seismically excited highway bridge［J］. Structural Control and Health Monitoring，2009，16(6):626－638.

［10］Li H，Liu M，Ou J P. Negative stiffness characteristics of active and semi-active control systems for stay cables［J］.Structural Control and Health Monitoring，2008，15(2):120－142.

［11］Ou J P，Li H.Analysis of capability for semi-active or passive damping systems to achieve the performance of active control systems［J］.Structural Control and Health Monitoring，2010，17(7):778－794.

［12］Wang Z H，Chen Z Q.Feasibility study of a self-powered magnetorheological damper for vibration control of a stay cable［C］//Advances in Environmental Vibration. Beijing:Science Press，2011:875－882.

［13］周亚刚，孙利民.斜拉索－三单元Maxwell 阻尼器系统的复模态分析［J］.同济大学学报:自然科学版，2006，34(1):7－12.

［14］陈政清，汪志昊. 基于能量回收的土木工程结构振动控制［J］.建筑科学与工程学报，2009，26(2):9－14.