基于JM模型的UMHexagonS算法的改进

贺艳春，林其伟

（华侨大学 信息科学与工程学院，福建 厦门 361021）

运动估计中的块匹配算法因运算简单、容易实现而成为目前运动估计的主流。其中的全搜索算法（FS），因其穷尽搜索每个像素点，搜索精度最高，但计算太复杂，不能满足实时性要求；而三步法（TSS）、四步法（FSS）以及交叉搜索法（CSS）等，相对FS，减少了搜索点数，满足实时性要求，但不利于小的运动块的搜索；新三步法（NTSS）、 六边形法 （HEX）、 钻石法 （DS）、 新四步法（NFSS）等，虽然提高了运动估计的速度，解决了早期算法不利于小运动块搜索的问题，但易陷入局部最优点，且不能很好地处理图像的运动类型[1]。针对这些问题，CHEN Z B等[2]人提出了UMHexagonS算法，它是一种混合型搜索算法，综合了非对称十字形法、六边形法、菱形法等，相对 FS，其均峰值信噪比（PSNR）保持基本不变，而运动估计时间减少了近90%，是目前运动估计搜索效率最高的快速搜索算法，己被JVT正式采纳。

1 UMHexagonS算法简介

UMHexagonS算法的搜索路径如图 1[3]所示，它主要分4步进行搜索：

（1）初始搜索点预测。包括中值预测、上层预测、前帧预测以及邻近参考帧预测，得到最佳的初始搜索点。

（2）以步骤（1）得到的最佳初始搜索点为中心，进行非对称的十字形搜索，取绝对差值和（SAD值）最小的点为当前最佳匹配点。其中水平方向的搜索范围为窗口宽度，垂直方向的搜索范围为窗口宽度的一半，如图1的step2所示。

（3）以步骤（2）得到的最佳匹配点为搜索中心，进行5×5共25点的正方形螺旋搜索，如图 1的 step3-1所示。接着进行多层六边形格点搜索，取最小SAD值所对应的点为最佳匹配点，如图1的step3-2所示。

（4）该步骤分两步进行：①以步骤（3）获得的最佳匹配点为搜索中心，进行扩展的六边形搜索。若当前最小SAD值点位于六边形的中心，则转到 b；否则返回 a继续进行六边形搜索，直到最小SAD值点位于六边形的中心，如图1的step4-1所示。②以步骤（3）的中心点为搜索中心，进行小菱形搜索，直到最小SAD值点位于小菱形的中心时，停止搜索，如图1的step4-2所示。

虽然UMHexagonS算法具有很高的编码效率，但仍存在两种不足：

（1）参考文献[4]中指出，在如图 2所示的 H.264的7种帧间预测模式中，有30.71%～98.03%的预测块的运动矢量全为0。若能在UMHexagonS算法进行搜索之前就判决出这些零运动矢量，就可以提前退出搜索，减少搜索时间。

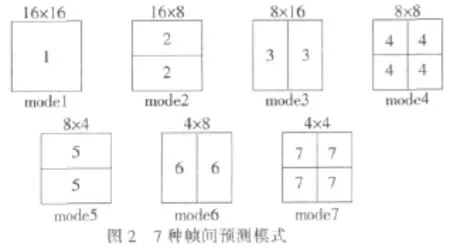
（2）候选搜索块的运动剧烈程度不同，其运动矢量的分布也不同。UMHexagonS算法对所有的候选搜索块都是进行4层16点的六边形搜索，没有考虑到候选搜索块的运动剧烈程度的不同，因此搜索存在冗余。

2 基于UMHexagonS算法的改进

（1）针对UMHexagonS算法的第一种不足，提出了零运动矢量提前判决的方法。

在进行初始搜索点预测时，最先进行中值预测，且所有的模板都可以使用中值预测，因此，可以判断中值预测得到的最佳匹配点mv（best_x，best_y）的 SAD值是否小于给定的阈值，若小于，则判决出该块的运动矢量为0。

定义SAD值为：

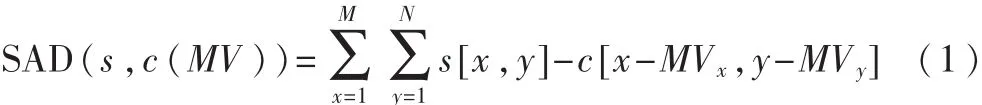
式中，s、c（MV）分别为编码的原始数据和编码重建的参考帧数据，MV为预测运动矢量。

本文定义点 mv（best_x，best_y）处的 SAD值满足式（2）时，则判定其运动矢量为0。

式中，Thresh[blocktype]是通过JM10.1的程序调试获得的经验阈值，表示7种帧间预测模式，取值为1，…，7。

（2）针对UMHexagonS算法的第二种不足，提出了自适应选择模板的方法。

[5]中指出，运动剧烈程度不同的块其运动矢量的分布也不同：若块的运动幅度较小，其运动矢量通常分布在离搜索中心较近的周围；若块的运动幅度中等，其运动矢量通常分布在离搜索中心较远的周围；若块的运动幅度很大，其运动矢量通常分布在远离搜索中心的周围。

因此，在UMHexagonS算法中，可通过判断块的运动剧烈程度，自适应地选择16点的六边形的搜索层数。但因为八边形比六边形更接近圆，所以将16点的六边形格点搜索减少为8点的八边形格点的搜索，如图3所示。

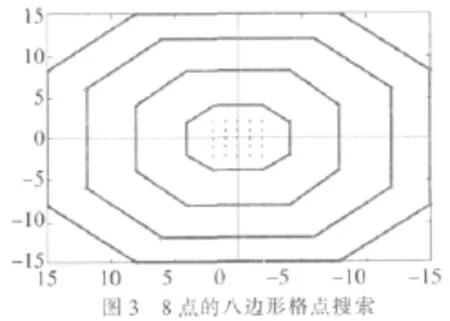
本文将当前模块的最小SAD值SADmin与自适应的阈值进行比较来确定其运动剧烈程度：平缓的运动、中等的运动以及剧烈的运动：

式中，pred_SAD为预测块的最小 SAD值，β2、β3为自适应系数，分别定义如下：

式中，blocktype取值1，…7，表示7种帧间预测模式。

因此，自适应模板选择过程如下：

（1）当模块的运动为平缓的运动时，选择 5×5小正方形以及2层8点八边形模板进行搜索。

（2）当模块的运动为中等的运动时，选择3层的8点八边形模板进行搜索。

（3）当模块的运动为剧烈的运动时，选择4层的8点八边形模板进行搜索。

由于非对称十字型搜索之后，需进行5×5的正方形搜索，以得到这一步的最佳匹配点。但是通过上面的分析可知，当模块的运动为中等的运动或者很剧烈的运动时，最佳匹配点在远离搜索中心点的周围，则5×5的搜索就没有必要了，只在模块的运动为平缓时，进行5×5的搜索。参考文献[6]中，5×5正方形的运动矢量分布如图4所示。

由图 4可知，5×5的正方形区域内，3×3的小正方形区域的运动矢量分布概率为71.792%，相对5×5的正方形区域的运动矢量的分布概率81.791%只减少了9.999%，而搜索点数减少了16点。因此，将5×5的正方形区域搜索改为3×3的小正方形区域搜索，能够在基本保证视频的质量的情况下，减少搜索点数，提高搜索速度。

改进后的算法流程图如图5所示。

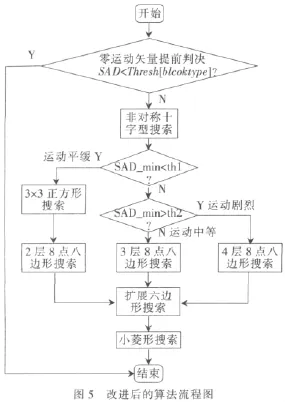
3 实验结果与分析

本文采用JM10.1模型进行测试，分别对运动剧烈的coastguard序列、运动中等的 foreman序列、运动平缓的news序列以及运动较复杂、细节较多、水平方向运动特征明显的Football序列进行了测试，这些序列都采用QCIF格式。编码100帧，IPPPP……编码模式，采用Hardmard变换，CABAC熵编码，QP取 28，选取 5帧参考帧。比较运动估计时间Me-time和峰值信噪比PSNR值。测试数据结果如表1所示。

表1中，△Me-time表示改进的 UMHexagonS算法的运动估计时间减去原UMHexagonS算法的运动估计时间得到的差值与原UMHexagonS算法的运动估计时间的百分比；△PSNR表示改进后与改进前的UMHexagonS算法的PSNR值的差值；△bit-rate/（kb/s）表示表示改进后与改进前的UMHexagonS算法的比特率的差值，正号表示增加，负号表示减少。由表1可知，改进后的算法与原算法相比，PSNR值基本保持不变，比特率有所增加，但是在误差允许的范围之内（±0.2 kb/s）；运动估计所消耗的时

表1 各种算法下的PSNR值和运动估计时间

间减少了10%～25%。达到了一定的改进效果。

本文通过分析UMHexagonS算法的一些不足，提出了零运动矢量提前判零、自适应选择水平方向和垂直方向搜索范围的相应的改进措施以及自适应的选择搜索模板。这样的改进在保证图像编码质量基本不变的情况下，减少了运动估计的搜索时间，从而提高了编码效率。

参考文献

[1]袁涛.基于 H.264运动估计算法的研究[D].重庆：重庆大学，2009.

[2]CHEN Z B，ZHOU P， HE Y.Fastintegerpeland fractional pel motion estimation for JVT[C].6th meeting：Awaji，Japan.JVT-F017，2002.

[3]毕厚杰.新一代视频压缩编码标准-H.264/AVC（第二版）[M].北京：人民邮电出版社，2009.

[4]陈桂兰，刘子坚.基于H.264的运动估计算法优化研究[J].濮阳职业技术学院学报，2010，23（2）：150-153.

[5]Xie Lifen，Huang Chunqing.UMHexagonS search algorithm forfastmotion estimation [C].IEEE， 3rd International conference on ICCRD 2011 3rd Intenational Conference on ICCRD，2011，4：483-487.

[6]LAM C H，PO L M，CHEUNG C H.A novel kite-crossdiamond search algorithm for fast block motion estimation[C].Proceeding s of 2004 IEEE International Symposium on Circuits and Systems.Canada： IEEE， 2004：729-732.