一种基于BP神经网络的数字识别新方法

刘 炀，汤传玲，王 静，石文莹，赵小兰

（合肥工业大学，安徽 合肥 230009）

神经网络是一种由简单单元组成的具有适应性的广泛并行互连的网络，其组织能够对真实世界物体做模拟生物神经系统的交互反应。神经网络已经成为一门比较重要的交叉性学科，被广泛应用于智能控制、模式识别、辅助决策、信号处理和计算机视觉等领域。BP（Back Propagation）神经网络在各门学科领域中都有非常重要的实用价值，也是在模式识别中应用最广泛的一种人工神经网络，它具有很强的自学习、自适应能力以及非线性逼近能力。由于基于误差梯度下降的BP算法易于陷入局部极小点而不收敛，目前，已经有很多学者对BP算法进行了研究，并针对它的这些缺陷提出了一些改进方法。

1 基本BP算法

1.1 BP算法原理

BP网络是采用误差反向传播算法的多层前馈网络，网络的输入和输出是一种非线性映射关系，其中，神经元的传递函数为Sigmod函数。

BP网络的学习规则是采用梯度下降算法。在网络学习的过程中，将输出层节点的期望输出（目标输出）与实际输出（计算输出）的均方误差一一逐层向输入层进行反向传播，再分配给各连接节点，并且计算出各连接节点的参考误差。在这个基础上可以调整各连接权值，使所获得的网络的期望输出与实际输出的均方误差达到最小。

将第j个样本输入到网络时，得到均方误差为：

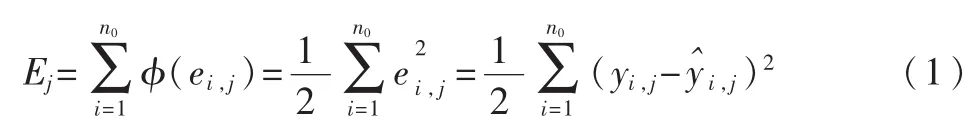
其中，ei，j表示输入第 j个样本时，输出层第 i个节点的期望输出值 yi，j与实际输出值间 的 差 值 ， 即 ei，j=yi，j-；n0为输出层的节点数。

连接权的调整主要有成批处理和逐个处理两种方法。成批处理是指一次性将所有训练样本输入，并计算总误差，然后调整连接权。逐个处理是指每输入一个样本就调整一次连接权值。本文采用逐个处理的方法，并根据误差的负梯度来修改连接权值。

BP网络的学习规则为：

设BP网络有1个隐含层，由神经元的输入与输出关系得：

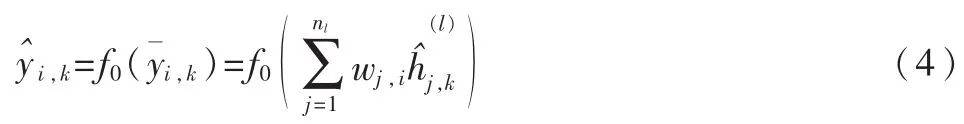
BP网络可以存储和学习大量的输入—输出模式映射关系，且无需事先揭示和描述这种映射关系的数学方程。在人工神经网络的实际应用中，很多神经网络模型就是采用BP网络及其变化形式的。

BP神经网络模型拓扑结构包括输入层、隐层和输出层3层，如图1所示。

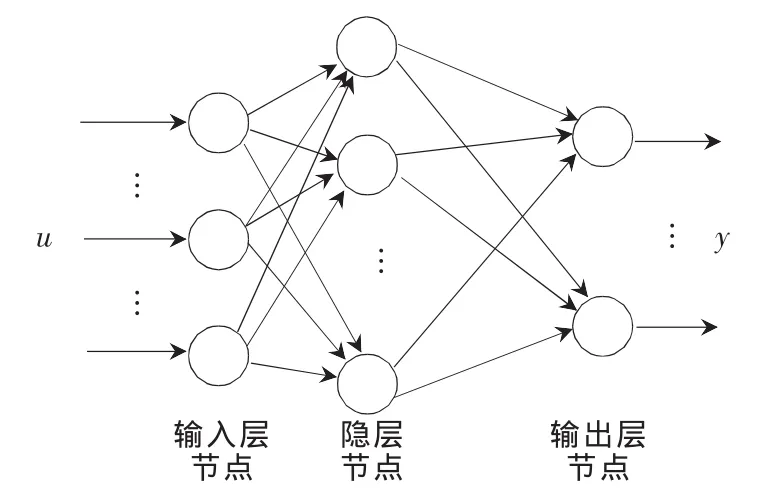
图1 BP神经网络拓扑结构

1.2 BP算法的程序实现

BP算法的程序实现的具体步骤如下：

（1）网络初始化。设计网络连接结构，规定输入变量和输出变量个数、隐含的层数和各层神经元的个数，对W（位于隐层到输出层之间）、权值矩阵V（位于输入层到隐层之间）赋随机数，将训练次数计数器q和样本模式计数 p置为 1，学习率 η设为 0～1内的小数，误差 E置0，网络训练后达到的精度Emax设为一个正的小数。

（2）输入训练样本对，利用现有的权值来计算网络中各神经元的实际输出。用当前样本xp、dp对d（期望输出向量）、向量数组 X（输入向量）赋值，用式（5）和式（6）计算O（输出层输出向量）和 Y（隐层输出向量）中各分量。

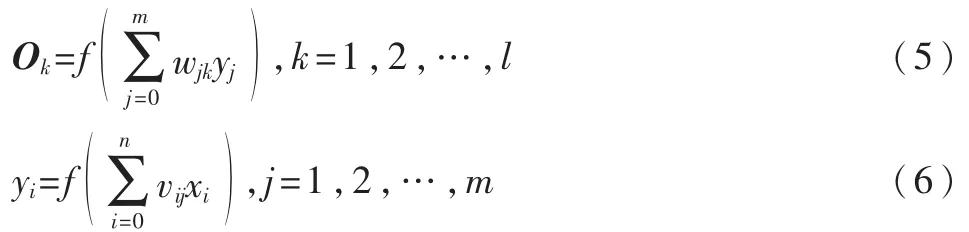
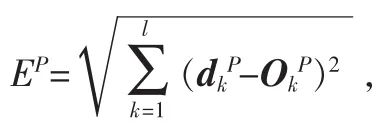
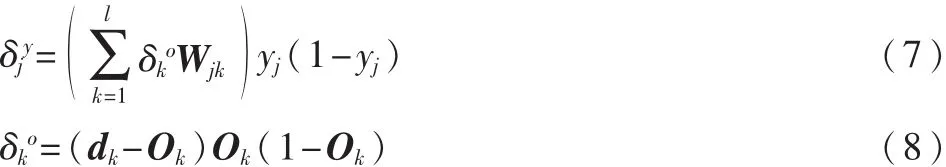
（5）各层权值间的调整。 应用式（9）和式（10）计算V、W中的各个分量。

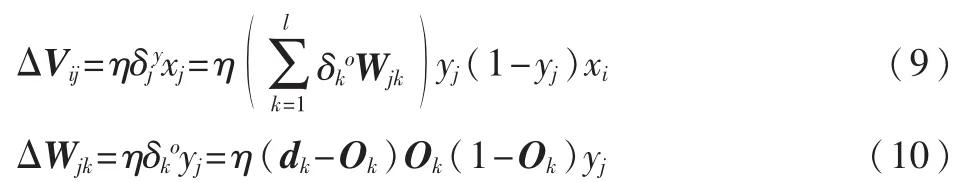
（6）检验是否对所有的样本完成了一次轮训。若p＜P，计数器 p、q 加 1，返回步骤（2）；否则，进行步骤（7）。

（7）检验网络总误差是否达到精度要求。如当用ERME作为网络的总误差时，若满足 ERME＜Emin，则训练结束；否则，E 置 0，p 置 1，返回步骤（2）。

2 BP算法的缺陷及其改进

2.1 BP算法的缺陷

3层前馈网络已经得到越来越广泛的应用，因为它有一个非凡优势，即将BP 算法用于具有非线性转移函数的3层前馈网络，可以以任意精度逼近任何非线性函数。但是标准的BP算法在应用中还有一些内在的缺陷：

（1）误差下降缓慢、迭代次数多、调整时间长，影响收敛的速度，会造成收敛速度慢，如果加快收敛速度则易于产生振荡。

（2）存在局部极小问题，但是却得不到全局最优。训练时会因陷入某个局部极小点而不能自拔，使得训练很难收敛在给定的误差内。

2.2 BP算法的改进

尽管标准的BP算法原理简单、实现方便，但由于训练过程中使用的是一个较小的常数，因此存在局部极小的点收敛速度慢问题。对于复杂的问题，训练过程则需要迭代几千甚至几万次才能将结果收敛到期望的精度。并且训练中的稳定性又要求学习率很小，因此梯度下降法会使得训练很慢。因此，标准的BP网络在很多方面表现出了不实用性，特别是对实时性很强的系统。鉴于传统的BP算法存在着以上的问题，国内外学者已经提出不少有效的改进方法，主要有两类：一类是基于标准梯度下降（如附加动量法、自适应学习率法等）进行改进；另一类是基于标准数值优化（如变步长法、牛顿法以及Levenberg-Marquardt算法等）进行改进。

2.2.1 基于变步长法改进

BP 算法之所以收敛速度慢，一个主要原因是学习速率η选取不当。η值选取过大，在算法收敛接近目标时易产生震荡，无法收敛到正确解；而η值选得过小，又会使整体学习速率变慢。因此，可以结合滤波器的思想设计一种自适应学习速率η。

假如第t-1次计算的误差为 εt-1，第t次计算的学习速率为 ηt，第 t+1 次计算的学习速率为 ηt+1，误差为 εt。可以定义 β=sgn（εt-εt-1），则 ηt+1=ηte-λβ。 其中，λ 为自适应系数，取值为 0.01～0.2；而 β实质上起到了一个滤波器的作用，导致误差减小的学习速率得以加强，反之则会被抑制。

2.2.2 基于牛顿法改进

由于梯度法在搜索过程中收敛速度较慢，牛顿法在这方面有所改进，它不但利用了准则函数在搜索点的梯度，还利用了它的二次导数。牛顿法的原理是求ε的二次近似的驻点，它用一个二次函数逼近ε，然后再求其驻点。若该函数为有强极小点的二次函数，它就能实现一步极小化。如果ε不是二次函数，则牛顿法一般就不能在一步内收敛。实际上根本无法确定它是否收敛，因为这取决于具体的函数和初始点。其主要改进是改变更新规则为：

2.2.3 基于Lebenberg-Marquardt算法改进

BP网络的训练实质是非线性目标函数的优化问题，基于数值优化的LM算法不但利用了目标函数的一阶导数信息，还利用了目标函数的二阶导数信息。LM算法的迭代公式为：

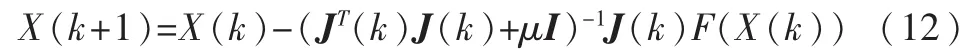
其中，I为单位矩阵，μ为阻尼因子，J是包含网络误差对权值和阈值一阶导数的Jacobin矩阵。

2.3 已提出的较好的改进方法

[1]中提出了将附加动量法和自适应学习率调整法两种策略结合起来的一种方法。这两种方法相结合既可有效地抑制网络陷入局部极小，又有利于缩短学习时间。但上述两种改进方法都是在标准梯度下降法基础上发展起来的，它们只利用了目标函数对网络权值和阈值的一阶导数信息。因此，当用于较复杂的问题时，仍存在收敛速度不够快的问题。

基于数值优化的LM算法是根据迭代的结果动态地调整阻尼因子，即动态地调整迭代的收敛方向，可使每次的迭代误差函数值都有所下降。它是梯度下降法和牛顿法的结合，收敛速度较快。但LM算法在计算过程中会产生大量的中间结果矩阵，因此，需要较大的内存空间，比较适宜中型网络使用。

可以考虑设计一个新的数字识别系统，以变步长法和牛顿法来改进BP算法，使其能够适应对数字样本组成的样本集的训练。

3 基于BP网络对数字识别系统的设计

本文采用逐像素特征提取方法提取数字样本的特征向量。设定归一化后的图像形成一个8×16的像素矩阵，依次取每列的元素转化为128×1的列矩阵，即数字字符的特征向量。这样把最后提取到的样本特征向量送到数字识别模块中，经过神经网络样本训练并记录下网络参数，最后对识别数据进行识别并给出结果。BP神经网络的数字识别系统数据处理流程如图2所示。

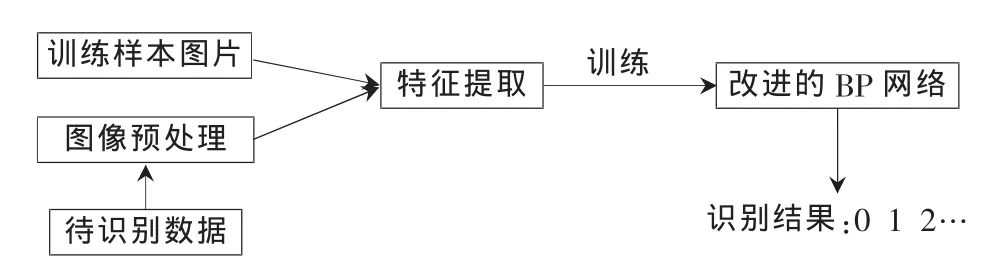
图2 BP神经网络的数字识别系统数据处理流程图

3.1 确定输入层神经元节点数

BP神经网络的输入层神经元节点数就是图像预处理后所输出的特征的个数。采用8×16的归一化处理以及逐像素特征提取方法，利用每个点的像素值作为特征，设定每个字符的标准归一化的宽度为 8，高度为 16，那么每个字符就有8×16=128个特征像素点，这样对于每个输入的样本，就有128个特征，由此可以确定输入层的节点数为128。

3.2 确定隐含层神经元节点数

相对而言，隐含层神经元节点数没有特别的要求，隐含层神经元的数目越多，BP 网络也就越精确， 训练时间也就会加长。然而，需要注意的是，隐含层节点不宜选取太多，否则会造成识别率的急剧下降，同时还会降低网络的抗噪声能力。到目前为止，隐含层的神经元的设定要不断地试验才有可能得到最佳的数目，在这里可以设定隐含层神经元的个数为10。

3.3 确定输出层神经元节点数

对数字字符，不管它的训练样本中有多少种字体，有多少个训练样本，也只有10个数需要编码，只需设定输出神经元个数为4就可满足2m≥N的条件。其中，m为输出层神经元个数，N是需要编码的训练样本个数。

由于采用S函数做激活函数，它的输出不可能达到0或1，只能是无限接近。可以在编码时做一个简单处理，将 0改为 0.1，1改为 0.9.

根据要求采用10个节点确定输入层的节点数，编码方案为：

4 实验结果与分析

在隐节点数一定的情况下，为了获得较好的泛化能力，存在一个最佳次数t0，这时会使得测试数据的均方误差最小。因此，可随意设置最小均方误差，本文设为0.000 1，设最大训练次数为16 000，这样就不会出现训练不足的情况，使其可以达到最小的均方误差。

4.1 改进前后的BP神经网络的性能比较

将参考文献[1]中提出的方法、基本BP算法与本文提出的方法进行实验数据比较，收敛速度比较如表1所示。

表1 3种算法比较

从表1可以看出，标准BP算法的收敛速度很慢，使用参考文献[1]中的方法可以加快网络收敛速度，而使用本文提出的新方法，速度比这两种方法更快。但由于本文提出的方法是两种基于数值优化方法的结合，它比参考文献[1]算法需要更大的内存空间，但需要的内存空间少于Lebenberg-Marquardt算法。因此，对于一个给定的问题，采用何种BP算法，取决于问题的复杂程度、训练样本数、权值以及阈值数目等各种因素。

参考文献

[1]王婷，江文辉，肖南峰.基于改进BP神经网络的数字识别[J].电子设计工程，2011，19（3）：108-112.

[2]万红，冯向荣，吕明相.改进BP算法在识别含噪声字符中 的 应 用 [J]. 微 计 算 机 信 息 ，2008，24 （10）：207-208，190.

[3]赵长青，李欧迅，黄书童.BP神经网络数字识别系统的设计方法 [J].桂林航天工业高等专科学校学报，2010（3）：292-294.

[4]施少敏，马彦恒，陈建泗.基于 BP神经网络的数字识别方法[J].网络与信息技术，2006，25（10）：40-41.