Delta工艺Inconel 718合金热变形条件下的流变行为

杨 平，赵玉涛，王安东，缪 栋，陈 刚，何 毅

(1. 江苏大学 材料科学与工程学院，镇江 212013；2. 丹阳精密合金厂，镇江 212352)

Delta工艺Inconel 718合金热变形条件下的流变行为

杨 平1，赵玉涛1，王安东1，缪 栋2，陈 刚1，何 毅1

(1. 江苏大学 材料科学与工程学院，镇江 212013；2. 丹阳精密合金厂，镇江 212352)

在Gleeble-3500热模拟实验机上对Delta工艺Inconel 718合金进行高温压缩实验，研究其高温压缩变形的流变应力行为。结果表明：δ相时效态Inconel 718合金在本实验条件下具有正的应变速率敏感性，流变应力随着应变速率的降低和变形温度的升高而减小，动态再结晶是合金重要的软化机制。δ相时效态Inconel 718合金的热变形激活能为497.407 kJ/mol，高温压缩峰值流变应力与变形温度和应变速率的关系可用双曲正弦函数表示。

Inconel 718合金；Delta工艺；高温压缩；流变应力；热变形激活能

Inconel 718(国内相应牌号为GH4169)是制造发动机涡轮盘、压气机盘等关键热端部件的重要材料，这类部件通常在高温和高压交互作用下工作，要求材料具有优良的抗低周疲劳性能。Inconel 718合金中 Nb的含量较高，容易形成偏析。通过锤或压力机锻造时，其工艺参数难以准确控制，因而其锻件的晶粒度粗细不均，即形成混晶组织而影响锻件的力学性能[1-2]。随着发动机安全性、可靠性要求的提高，获得组织细小均匀的锻坯及盘锻件成为关键。

Inconel 718合金中以γ″作为主要强化相，δ相是γ″相的平衡相，也是Inconel 718合金的主要组成相之一。δ相的形貌、数量和分布对于合金的疲劳性能、持久性能、抗缺口敏感性和热加工性能有很大影响[3-6]。一般认为，呈粒状均匀分布适量的δ相有利于合金的力学性能。由于δ相钉扎晶界、阻止晶粒长大的作用[7]，RUIZ等[8]提出了经δ相析出处理后再进行热形变的 Delta工艺，通过适当热加工工艺能够获得组织均匀细小的大尺寸Inconel 718锻坯件。

在热变形行为及工艺研究方面，THOMAS等[9]在对Inconel718合金高温热变形研究时发现，合金的流变行为与位错的运动、动态析出和 Ni元素的自扩散有关。KASHYAP和 CHATURVEDI[10]求出了Inconel718合金高温塑性变形的激活能。WANG等[11-12]研究了Inconel718合金在热变形条件下流变行为、组织及 Delta工艺下该合金的热加工特性及动态再结晶。DIX等[13]利用Delta工艺获得了晶粒尺寸等级为9级的Inconel 718合金锻坯，并通过闭模锻造获得了晶粒尺寸为 13级的涡轮盘锻件。BHOWAL和SCHIRRA[14]将Delta工艺和Gatorizing工艺相结合获得了晶粒尺寸等级高于11级的Inconel 718合金涡轮盘锻件。吕宏军等[15]通过 Delta工艺轧制得到了晶粒度为12～14级的超细晶合金板坯。在Inconel 718合金热加工过程中，等温锻造虽然能够实现较好控制，但其成本很高，在国内尚很少应用。若能在 Delta工艺中通过普通非等温锻造使Inconel 718合金获得细小均匀的锻造组织，将具有非常重要的意义。本文作者通过热压缩实验，采用两步锻造工艺模拟实际生产过程，研究Delta工艺Inconel 718合金在不同变形温度和应变速率下的流变行为，确定其本构方程，以期为该合金加工工艺的研究和优化提供依据。

1 实验

试验用Inconel 718合金坯料，其生产方法采用真空感应熔炼+电渣重熔，主要化学成分(质量分数，%)如下：C 0.03, Ni 51.09, Cr 19.14, Nb 5.07, Mo 3.09, Al 0.67, Ti 1.09, Si 0.20, B 0.0037, S 0.0045, Mn 0.14, Fe余量。

将试样在1 040 ℃保温1 h进行均匀化固溶处理后水冷至室温，以保证试样的微观组织为奥氏体固溶体和少量的碳化物。δ相的析出峰温度为 890～900℃，本试验选择在900 ℃时效24 h析出大量δ相。

将固溶和时效处理后的试样加工成 d 8 mm×15 mm的圆柱状试样。热压缩实验在Gleeble-3500热模拟实验机上进行，并在试样两端垫石墨片及钽片以减小摩擦对应力状态的影响。Inconel 718合金的热加工温度通常在900～1 100 ℃之间，本试验热压缩温度(开始变形至终了变形温度)为1 050～980 ℃、1 020～950℃和980～920 ℃；采用70%的总变形量，在开始变形和终了变形温度下的变形量分配分别为 20%～50%、35%～35%和50%～20%；变形速率选择10、1、0.1和0.01 s-1。热模拟试验的升温速率为10 ℃/s，第一步保温时间为3 min，第二步保温时间为2 min，试样经变形后气冷。

2 结果与分析

2.1 真应力—真应变曲线

δ相时效态Inconel 718合金在不同变形条件下的真应力—真应变曲线如图1和2所示。根据真应力—真应变曲线形状可以初步判定，δ时效态Inconel 718合金在试验条件下发生了动态再结晶。在开始变形阶段，位错密度随着变形程度的增加而不断增大，位错间的交互作用又增大了位错运动的阻力，从而流变曲线表现出加工硬化特征。随着变形程度的不断增加，超过某一形变量后，累积的变形储存能超过再结晶所需驱动力，发生动态再结晶软化，当软化速率与硬化速率平衡时，流变应力达到最大值；随着再结晶的进行，当软化速率大于硬化速率时，流变应力逐渐下降。这种下降趋势在第二步变形中不太明显，在第二步变形中，流变应力达到峰值后稍微下降或呈现平稳状态。同时从图1和2可以看到：在同一变形温度下，随应变速率的增加，峰值应力增大；在同一应变速率下，随变形温度的升高，峰值应力明显下降，说明δ相时效态Inconel 718合金在本实验条件下具有正的应变速率敏感性。

2.1.1 应变速率对Inconel 718合金流变应力的影响

图1所示为δ相时效态Inconel 718合金在不同应变速率下的真应力—真应变曲线。由图1可见：在相同温度下，随着应变速率的降低，流变应力显著降低。在较高(10 s-1)和较低应变速率(0.01 s-1)下，随变形的进行，超过峰值应变后流变软化速率大于硬化速率，曲线下降趋势明显。而当应变速率为1 s-1和0.1 s-1时，流变应力随变形程度的增大下降较平缓，流变软化速率略大于硬化速率。

应变速率对流变应力的影响在于：应变速率的增加会使位错运动速度增大，从而提高变形抗力；应变速率的提高一方面能够促进再结晶的发生，另一方面使变形时间缩短，减少了再结晶形核和晶粒长大的时间，因此，应变速率对流变应力的影响受这几方面的综合作用。

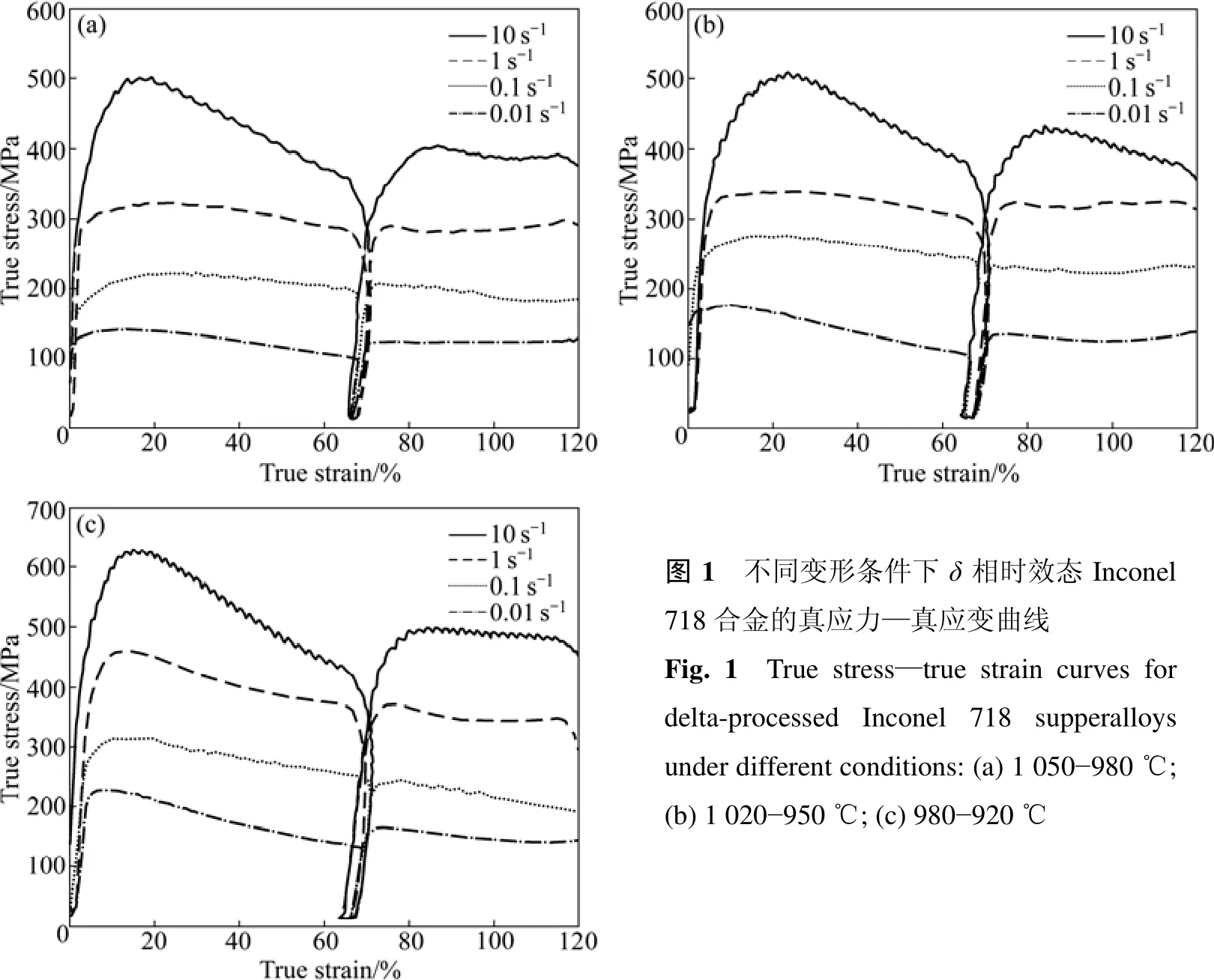
图1 不同变形条件下δ相时效态Inconel 718合金的真应力—真应变曲线Fig.1 True stress—true strain curves for delta-processed Inconel 718 supperalloys under different conditions: (a) 1 050-980 ℃;(b) 1 020-950 ℃; (c) 980-920 ℃

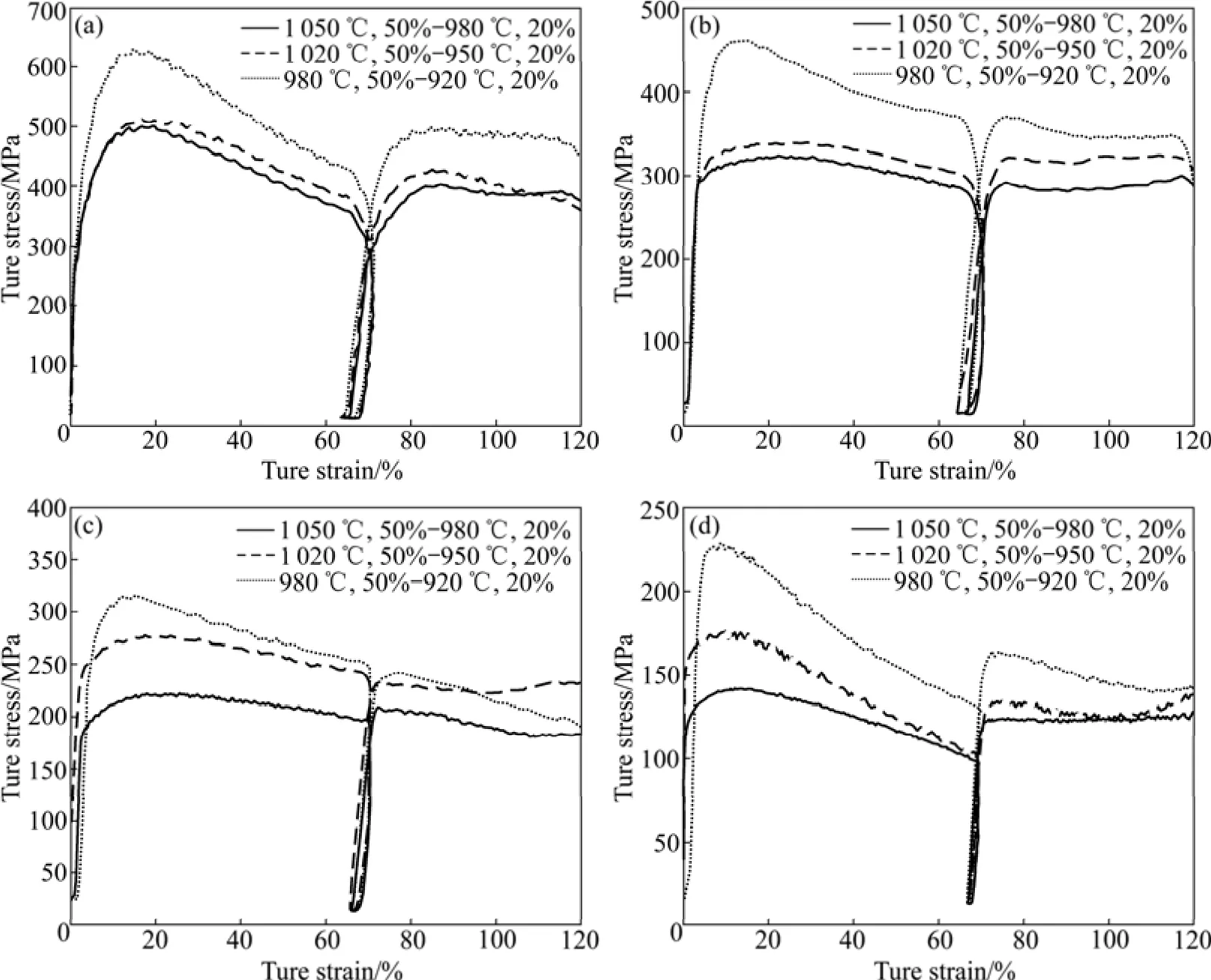
图2 不同变形条件下δ时效态Inconel 718合金在不同应变速率下的真应力—真应变曲线Fig.2 True stress—true strain curves for delta-processed Inconel 718 superalloys compressed at different deformation temperatures and stain rates: (a) 10 s-1; (b) 1 s-1; (c) 0.1 s-1; (d) 0.01 s-1

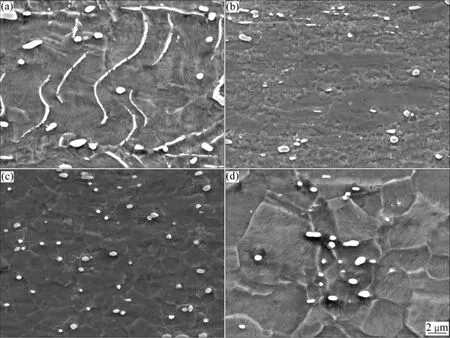
图3 Inconel 718合金在不同应变速率下热变形后的显微组织Fig.3 Optical microstructures of Inconel 718 supperalloys compressed at 1 050-980 ℃, 35%-35% and different strain rates:(a) 10 s-1; (b) 1 s-1; (c) 0.1 s-1; (d) 0.01 s-1

图3 所示为Inconel 718合金在不同应变速率下热变形后的显微组织。从图3(a)看出，变形作用使δ相内部的亚晶界或高位错密度区增多，从而促进δ相溶解断裂，开始溶解，并出现部分再结晶。图3(b)中出现了明显的混晶组织，这是由于应变速率较大，动态回复率低，位错增殖率增加，形变组织中的位错密度大，积聚的形变储存能也大，因而易形成不均匀的组织。当应变速率为 0.1 s-1时，再结晶已完全进行，δ相呈颗粒均匀分布在晶界周围，如图 3(c)所示。而当应变速率为0.01 s-1时，只有少量δ相分布在晶界，晶粒明显长大，如图3(d)所示。

2.1.2 变形温度对Inconel 718合金流变应力的影响

由不同变形温度下δ时效态Inconel 718合金的真应力—真应变曲线(图 2)可见：在相同的应变速率和应变下，较高温度下其流动应力及峰值应力较小。在较高应变速率(10 s-1、1 s-1)，温度从1 050 ℃下降到1 020 ℃时其流变应力和峰值应力仅略微增大，而在较低应变速率下(0.1 s-1、0.01 s-1)，流变应力增大明显。温度对流变应力的影响主要在于：一方面温度的升高使原子动能增加，原子热振动的振幅增大，原子间的结合力变弱，从而使临界剪切应力降低；另一方面温度的升高使热激活作用增强，从而使激活能控制的再结晶形核速率及晶核长大的驱动力增大，同时较高的温度有利于位错的攀移、交滑移和位错结点脱锚，因此，温度的升高促进和增强回复与动态再结晶的发生，从而使流变应力降低。图 4所示为合金在变形量为50%～20%时不同变形温度下的显微组织。可见，在同一应变速率下，温度的升高在促使δ相溶解的同时，还能促进热变形合金的动态再结晶和晶粒长大。

2.2 δ时效态Inconel 718合金的本构方程

金属和合金的高温塑性变形是一个受热激活控制的过程。热变形过程中，材料在任何应变或稳态下的高温流变应力σ强烈地取决于变形温度T和应变速率ε˙。其流变行为可用应变速率ε˙、温度T和流变应力σ之间的关系进行描述。

结合 Zener-Hollomon 参数[16]Z=ε˙exp[Q/(RT)]，通常采用以下3种Arrhenius关系表示材料的本构关系：

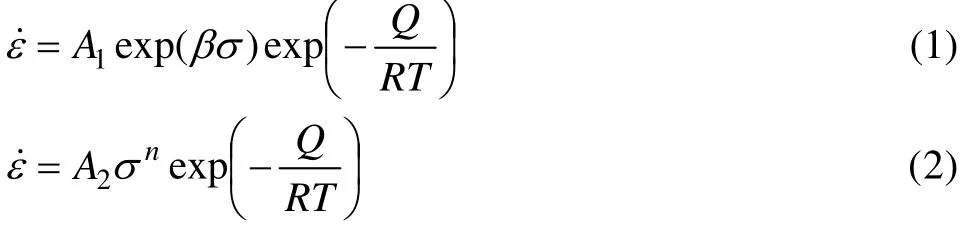
图4 Inconel 718合金在不同变形温度下热变形后的显微组织Fig.4 Optical microstructures of Inconel 718 supperalloys compressed under different conditions: (a) 980-920 ℃, 0.1 s-1;(b) 1 020-950 ℃, 0.1 s-1

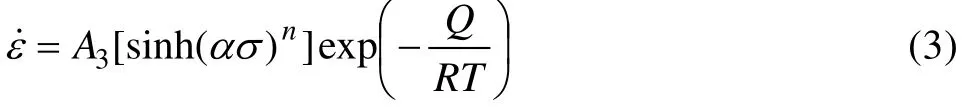
且α、β和n之间满足关系：

式中：Q为变形激活能；σ为稳态或峰值应力；R为摩尔气体常数；α为应力水平参数；β为应变参数；n为应力指数；A1、A2和A3均为结构因子。

其中，幂指数关系式(1)适用于高应力水平(ασ＞1.2)；指数关系式(2)适用于低应力水平(ασ＜0.8)；双曲正弦关系式(3)是在式(1)和(2)的基础上提出的一种修正式[17-18]，适用于较宽范围的应力水平。

对式(1)～(3)两边分别取对数，可得：

假设δ时效态Inconel 718合金高温压缩流变应力与应变速率分别满足上述3种关系，将其峰值应力与应变速率数据(名义应变为35%(真应变67%)时，下同)分别代入式(5)～(7)，并采用最小二乘法进行线性回归处理，可得到相应的 σ—lnε˙和 ln σ—lnε˙的关系曲线，分别如图5(a)和(b)所示。由式(5)和(6)可知，当温度一定时，1/β 和 1/n 分别为 σ—lnε˙和 ln σ—lnε˙曲线的斜率。根据式(4)得到α值，代入峰值应力和应变速率数据可得到 ln[sinh(ασp)]—lnε˙曲线如图 5(c)所示。

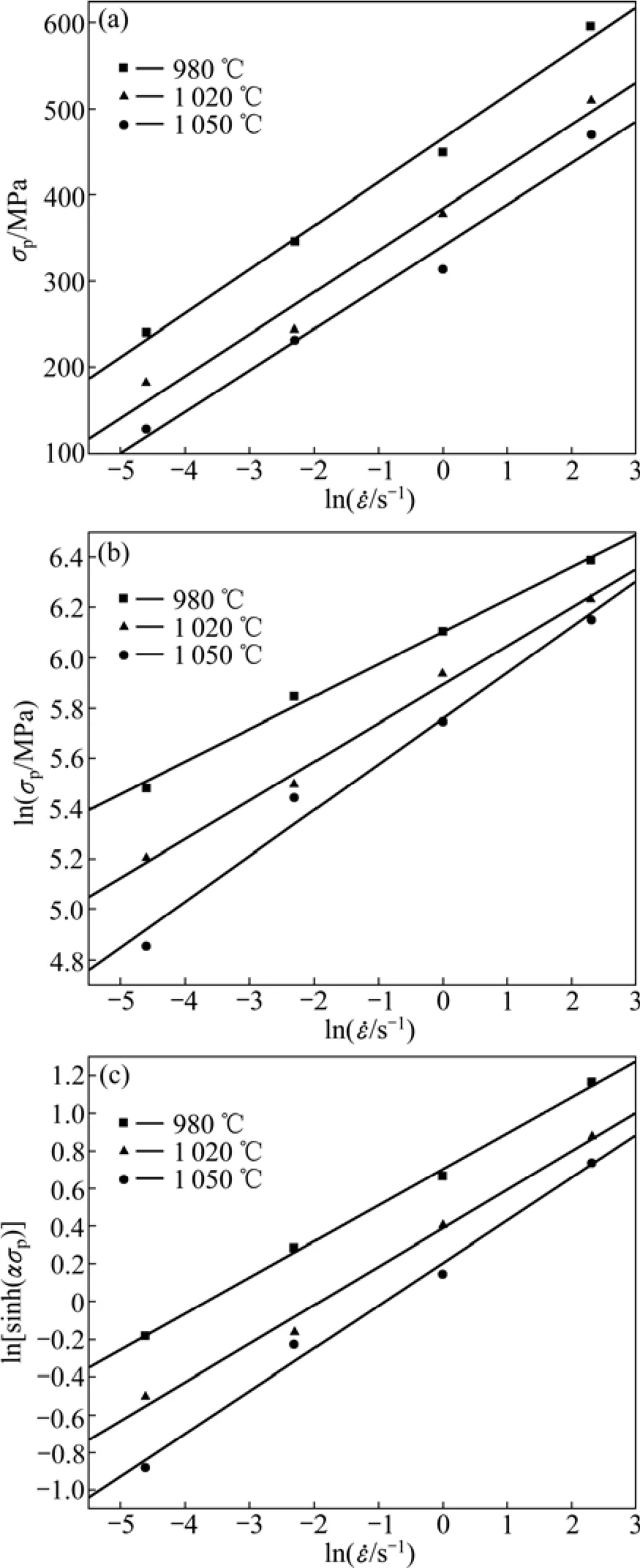
图5 δ相时效态Inconel 718合金高温压缩峰值应力与应变速率的关系Fig. 5 Relationship between peak stress and strain rate of delta-processed Inconel 718 supperalloys: (a) σp—lnε˙;(b) ln σp—lnε˙; (c) ln[sinh(ασp)]—lnε˙

将δ相时效态Inconel 718在不同应变速率下峰值应力与变形温度的数据代入并进行线性回归处理，得到流变应力与变形温度的关系如图6所示。

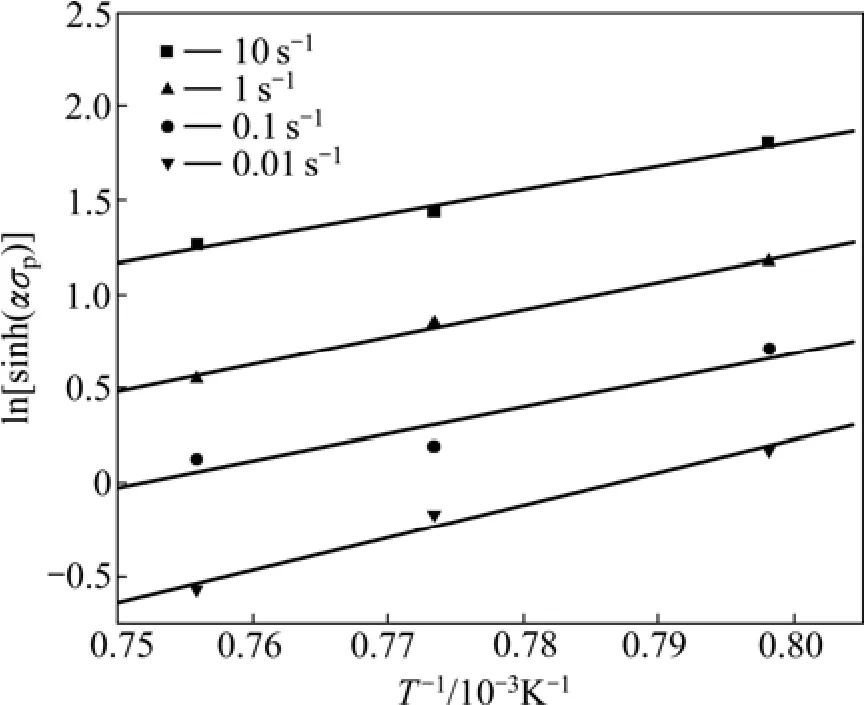
图6 δ相时效态Inconel 718合金高温压缩峰值应力与变形温度的关系Fig. 6 Relationship between peak stress and deformation temperature of delta-processed Inconel 718 supperalloys

根据图5的线性回归结果得到不同温度下δ相时效态Inconel 718合金在热压缩变形过程中的参数α、n和β(见表1)。α与各变形条件下的峰值真应力σp的乘积ασ列于表2。

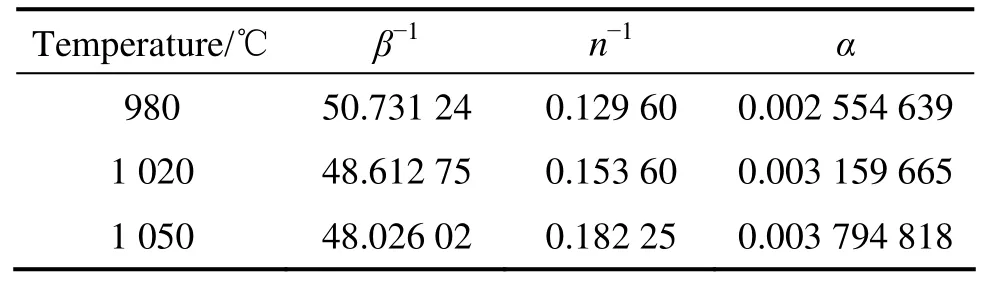
表1 不同温度下Inconel 718合金的热压缩变形常数Table1 Constants of delta-processed Inconel 718 supperalloys at different deformation temperatures

表2 不同变形条件下Inconel 718合金的ασp值Table 2 ασp values of Inconel 718 supperalloys under different deformation conditions

由表2可知，应变速率为10 s-1以及应变速率为1 s-1且变形温度≤980 ℃时，属于高应力水平下的变形，符合幂指数公式(5)；当应变速度为0.01 s-1以及应变速率为0.1 s-1且变形温度≥1 020 ℃时，属于低应力水平下的变形，符合指数公式(6)。

对式(7)两边求导，可得变形激活能 Q的表达式如下：

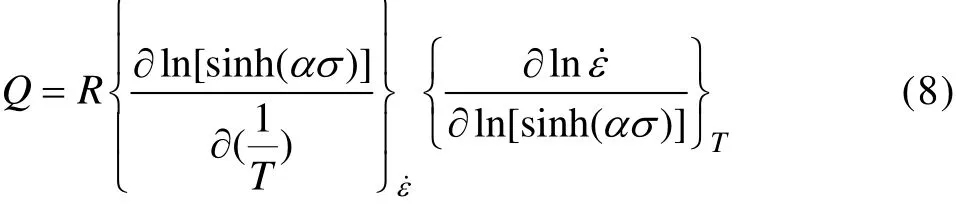
如前所述，由图 5(a)中 σp—lnε˙拟合曲线的斜率得出 β0=0.020 4；由图 5(b)中 ln σp—lnε˙拟合曲线的斜率得到 n0=6.446，根据式(4)，则 α0=β0/n0=0.003 16。由式(7)可知，当温度一定时，ln[sinh(ασp)]—lnε˙呈线性关系。将α0值与应变速率和峰值应力值代入式(7)，用最小二乘法线性回归得到ln[sinh(ασp)]—lnε˙的斜率(见图 5(c))，取其平均值 n1，则根据式(4)得到一个调整后的 α1值。将 α1值重新代入式(7)，绘制相应的ln[sinh(ασp)]—lnε˙和 ln[sinh(ασp)]—1/T 图，用最小二乘法线性进行回归，分别取直线斜率的倒数和直线斜率平均值得到相应的 n2和 k1值。重复上面的迭代步骤，直至n值的平均偏差最小，此时得到的材料常数更为真实可靠。

利用上述方法求得：α=0.007 99，n=2.484，Q=497.407 kJ/mol。

将Q值代入Z参数表达式，则有Z=ε˙exp[497 407/(RT)]。

将式(8)代入式(3)得：

对式(9)两边取自然对数，则

即有

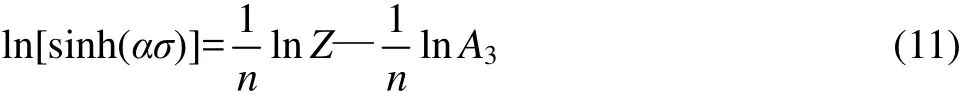
可见，1/n为直线的斜率，-(1/n)ln A3为直线的截距。

将所求得的Q值、试验数据ε˙和T值代入式(8)，可得到对应的ln Z值。取ln Z和对应的ln[sinh(ασp)]，用最小二乘法线性回归法绘制相应的 ln[sinh(ασp)]—ln Z曲线，如图 7 所示，根据直线截距可得 A3=4.177×1016。

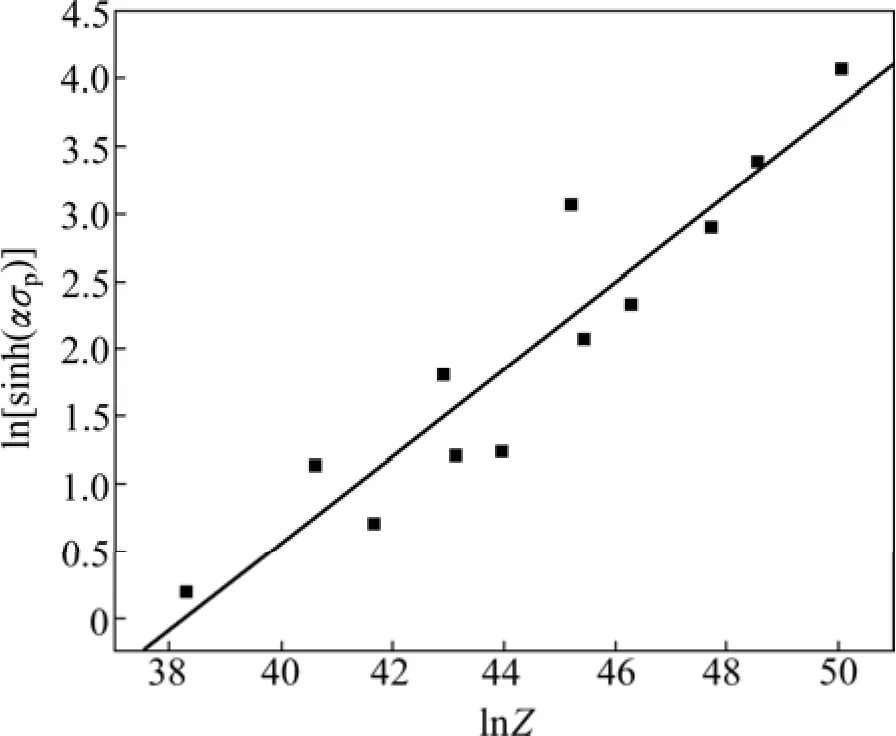
图7 δ相时效态Inconel 718合金高温压缩峰值应力与Z参数关系Fig. 7 Dependence of peak stress on Z parameter of deltaprocessed Inconel 718 superalloys

由此，可以得到δ相时效态Inconel 718合金高温压缩本构方程为

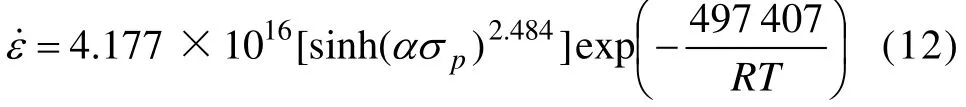
3 结论

1) 在相同温度下，随着应变速率的降低，δ相时效态 Inconel 718合金的流变应力显著降低。在较高(10 s-1)和较低(0.01 s-1)应变速率下，随变形的进行，超过峰值应变后流变软化速率大于硬化速率的几率大，曲线下降趋势明显。而在应变速率分别为1 s-1和0.1 s-1时，流变应力随变形程度的增大下降较平缓，流变软化速率稍大于硬化速率。

2) 在相同的应变速率和应变下，较高温度下合金的流变应力及峰值应力较小。在较高应变速率下(10 s-1，1 s-1)，温度从1 050 ℃下降到1 020 ℃时其流变应力和峰值应力略微增大，而在较低应变速率下(0.1 s-1，0.01 s-1)，流变应力增大较多。

3) δ相时效态Inconel 718合金的热变形激活能为497.407 kJ/mol，其峰值流变应力与变形温度和变形速率的关系可用如下公式描述：

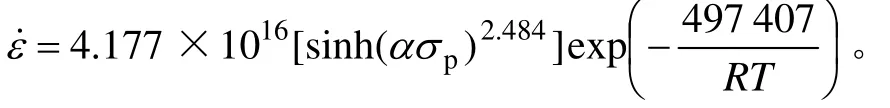
REFERENCES

[1] 庄景云, 杜金辉, 邓 群. GH4169合金及其锻件晶粒形貌的特点[J]. 钢铁研究学报, 2003, 15(7): 44-48.ZHUANG Jing-yun, DU Jin-hui, DENG Qun. Grain morphologies characteristics of alloy GH4169 and forgings[J].Journal of Iron and Steel Research, 2003, 15(7): 44-48.

[2] 刘 东, 罗子健. GH4169合金锻件的混晶组织[J]. 热加工工艺, 2004(9): 3-5.LIU Dong, LUO Zi-jian. Mixed grain structrue of GH4169 alloy forgings[J]. Hot Working Technology, 2004(9): 3-5.

[3] CAI D Y, ZHANG W H, NIE P L, LIU W C, YAO M.Dissolution kinetics of δ phase and its influence on the notch sensitivity of Inconel 718[J]. Materials Characterization, 2007,58(3): 220-225.

[4] 洪班德, 伊 晓, 孟庆昌. δ-Ni3Nb对Inconel 718合金低周疲劳断裂行为的影响[J]. 金属学报, 1991, 27(1): 55-60.HONG Ban-de, YI Xiao, MENG Qing-chang. Effect of δ-Ni3Nb on low cycle fatigue racture of Inconel 718[J]. Acta Metallurgica Sinica, 1991, 27(1): 55-60.

[5] 周晓虎. GH4169合金涡轮盘锻件粗晶质量分析和控制[J]. 锻造, 2004(5): 9-11.ZHOU Xiao-hu. Analysis and control of coarse grain formation of GH4169 alloy turbine wheel[J]. Forging, 2004(5): 9-11.

[6] HUANG YI, LANGDON T G. The evolution of delta-phase in a superplastic Inconel 718 alloy[J]. Full Journal of Materials Science, 2007, 42(2): 421-427.

[7] MURALIDHARAN G, THOMPSON R G. Effect of second phase precipitation on limiting grain growth in alloy 718[J].Scripta Materialia, 1997, 36(7): 755-761.

[8] RUIZ C, OBABUEKI A, GILLESPIE K. Evaluation of the microstructure and mechanical properties of delta-processed alloy 718[C]//Proceedings of Superalloys 1992. Warrendale:TMS, 1992: 33-42.

[9] THOMAS A, EI-WAHABI M, CABRERA J M, PRADO J M.High temperature deformation of Inconel 718[J]. Journal of Materials Processing Technology, 2006, 177: 469-472.

[10] KASHYAP B P, CHATURVEDI M C. Activation energy for superplastic deformation of In718 superalloy[J]. Scripta Mater,2000, 43: 429-433.

[11] WANG Y, SHAO W Z, ZHEN L, YANG L, ZHANG X M. Flow behavior and microstructures of superalloy 718 during high temperature deformation[J]. Materials Science and Engineering A, 2008, 497: 479-486.

[12] WANG Y, ZHEN L, SHAO W Z, YANG L, ZHANG X M. Hot working characteristics and dynamic recrystallization of delta-processed superalloy 718[J]. Journal of Alloys and Compounds, 2009, 474: 341-346.

[13] DIX A W, HYZAK J M, SINGH R P. Application of ultra fine grain alloy 718 forging billet[C]//Proceedigns of Superalloys 1992. Warrendale: TMS, 1992: 23-32.

[14] BHOWAL P R, SCHIRRA J J. Full scale GatorizingTMof fine grain Inconel 718[C]//Superalloys 718, 625, 706 and Various Derivatives. Warrendale: TMS, 2001: 193-201.

[15] 吕宏军, 姚草根, 张凯峰, 贾新朝. GH4169合金细晶成型工艺与机理及性能研究[J]. 机械工程材料, 2003, 27(1): 15-17,50.LÜ Hong-jun, YAO Cao-gen, ZHANG Kai-feng, JIA Xin-chao.Fine-grain forming process, mechanism and properties of GH4169 alloy[J]. Materials for Mechanical Engineering, 2003,27(1): 15-17, 50.

[16] ZENER C, HOLLOMON J H. Effect of strain-rate upon the plastic flow of steel[J]. Applied Physics, 1944, 15(1): 22-27.

[17] WANG Y, LIN D L. A correlation between tensile flow stress and Zener-Hollomon factor in TiAl alloy at high temperatures[J].Materials Science, 2000, 19: 1185-1188.

[18] SHI H, MCLAREN A J, SELLARS C M, SHAHANI R,BOLINGBROKE R. Constitutive equations for high temperature flow stress of aluminum alloys[J]. Materials Science and Technology, 1997, 13(3): 210-216.

Flow stress behavior of delta-processed Inconel 718 superalloy under hot compression deformation

YANG Ping1, ZHAO Yu-tao1, WANG An-dong1, MIAO Dong2, CHEN Gang1, HE Yi1
(1. School of Materials Science and Engineering, Jiangsu University, Zhenjiang 210213, China;2. Danyang Precision Alloy Factory, Zhenjiang 212352, China)

The flow stress behavior of the delta-processed Inconel 718 superalloy was investigated by the hot compression on Gleeble-3500 test machine. The results of the thermal simulation compression tests show that the flow stress is positively sensitive to the strain rate and the deformation temperature. The peak stress decreases with the decreasing strain rate and increasing deformation temperature. The dynamic recrystallization is the main softening mechanism of the hot deformation of the delta-processed Inconel 718 superalloy. The activation energy (Q) of the delta-processed δ phase aged Inconel 718 superalloy is 497.407 kJ/mol. The relationships among the flow stress, the deformation temperature and the strain rate for the delta-processed Inconel 718 can be described by the hyperbolic sine-type function.

Inconel 718 superalloy; delta process; hot compression; flow stress; hot deformation activation energy

TG111.7

A

1004-0609(2012)1-0072-08

江苏省科技成果转化项目(BA2007104)；江苏省先进金属材料高技术研究重点实验室开放课题资助项目(AMM200902)

2010-12-14；

2011-04-01

赵玉涛，教授, 博士；电话：0511-88797658; E-mail: zhaoyt@ujs.edu.cn

(编辑 陈卫萍)