基于改进GM(1,1)模型的沉降监测数据处理方法探讨

2012-11-22王家帮广西国土资源规划设计院广西南宁530022

长江大学学报(自科版) 2012年25期

关键词：原始数据算子线性

王家帮 (广西国土资源规划设计院，广西南宁 530022)

黄长军 (湖南城市学院市政与测绘工程学院, 湖南益阳 413000；武汉大学测绘学院，湖北武汉 430079)

咸茂鲜 (广西国土资源规划设计院，广西南宁 530022)

曹元志 (湖南城市学院市政与测绘工程学院, 湖南益阳 413000)

基于改进GM(1,1)模型的沉降监测数据处理方法探讨

王家帮 (广西国土资源规划设计院，广西南宁 530022)

黄长军 (湖南城市学院市政与测绘工程学院, 湖南益阳 413000；武汉大学测绘学院，湖北武汉 430079)

咸茂鲜 (广西国土资源规划设计院，广西南宁 530022)

曹元志 (湖南城市学院市政与测绘工程学院, 湖南益阳 413000)

在分析GM(1,1)预测模型存在不足的基础上，提出了GM(1,1)模型的改进形式。运用序列算子作用和加权均值的方法来增强原始序列数据的光滑度；考虑到沉降监测数据序列既含有线性趋势又有指数增长趋势，用GM(1,1)和线性回归的组合模型对其进行建模和分析。实例分析表明，改进后的GM(1,1)模型可以提高预测精度，从而满足工程实际要求。

GM(1,1)模型；序列算子作用；加权均值；线性回归

近年来，用数学模型来逼近、模拟和揭示变形特性，进而进行相应预测已成为新的研究趋势。但由于模型本身的局限性，导致预测精度不高。目前，有关学者提出GM(1,1)模型的改进方法[1]，但没有充分考虑模型中序列数据出现异常的情况，而实际生活中有很多因素会对沉降监测数据序列有所影响,使得序列数据出现异常，若仍用原有数据序列进行建模预测，势必会出现很大的偏差而影响预测精度[2]。针对上述情况，笔者基于改进GM(1,1)模型对沉降监测数据处理方法进行了探讨。

1 GM(1,1)模型概述

1.1GM(1,1)模型的建立

设有非负原始时间序列x(0)(k)={x(0)(1),x(0)(2),…,x(0)(n)}，对原始时间数据序列作一次累加生成序列：

x(1)=AGOx(0)x(1)(k)={x(1)(1),x(1)(2),…,x(1)(n)}

(1)

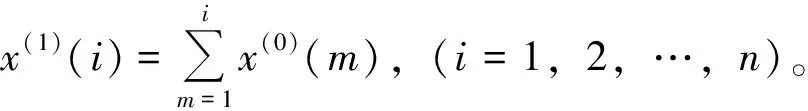
GM(1,1)模型的灰微分方程为：

x(0)(k)+az(1)(k)=b

(2)

式中，z(1)(k)=(x(1)(k-1)+x(1)(k))/2(k=2,3,…,n)称为白化背景值；a为发展系数；b为灰作用量，其对应的白化微分方程为：

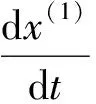
(3)

根据最小二乘法原理，式(2)的参数可求出：

(4)

(5)

(6)

当t=1,2，…，n时，式(5)即为式(3)的离散形式解，此时：

(7)

式中，x(0)(k)(k=1,2，…，n)是原始数据序列的拟合值。

1.2GM(1,1)模型的局限性分析

①GM(1,1)模型的拟合与预测精度取决于参数a和b，而a和b的值又依赖于原始序列和背景值的构造形式。在实际建模的过程中，需要先对原始序列进行级比平滑检验，该序列只有在满足光滑性要求的前提下，建模预测的结果才会较为准确，否则建模预测的结果不准确。②建模时用指数函数来模拟生成数据，这要求原始数据服从一定的分布，但只适用于变形呈指数趋势变化情况，而对在趋势线上发生跳变的序列数据出现异常(如指数偏离过大甚至减小)的情况则没有考虑。

2 GM(1,1)模型的改进

2.1序列算子作用下的GM(1,1)模型

设原始数据序列为x(0)(k)={x(0)(1),x(0)(2),…x(0)(n)}，一阶弱化算子XD1和一阶强化算子XD2：

XD1={x(1)d1,x(2)d1，…,x(n)d1}XD2={x(1)d2,x(2)d2,…,x(n)d2}

为一阶作用算子序列，其中：

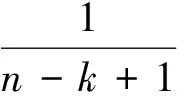
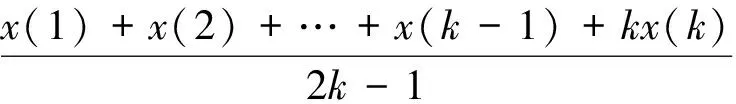
弱化算子D1会使原始序列X的变化速度变慢, 强化算子D2会使原始序列数据变化速度加快，相应的，XD1D1为二阶弱化算子,XD1D1为二阶强化算子。研究表明，强化算子与弱化算子都能使序列增加光滑性[6]。

2.2GM(1,1)与线性回归组合模型

为解决GM(1,1)预测中存在的数据跳变问题,利用线性回归适用短期预测的特点,提出了一种新的预测方法，即用GM(1,1)模型预测将来可能的数据跳变日期点,对其他非跳变点则使用分段线性回归函数进行预测。

1)设原始序列X(0)和历史数据Q(0)为：

X(0)={x(0)(q(1)),x(0)(q(2)),…x(0)(q(n))}Q(0)={q(1)，q(2)，…，q(n)}

2)以原始序列为依据画出折线图，以q(i)为x轴，以x(0)(q(i))为y轴。

3)观察折线图，从原始序列中选择跳变点，跳变日期点和跳变值分别组成跳变日期原始序列和跳变原始序列。

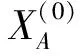
其中，ap、bp分别为跳变函数的参数；ax、bx分别为预测涵数的参数。

5)运用跳变预测函数预测下面若干个跳变日期和跳变值：

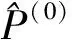
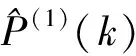
6)当预测日期是预测跳变日期点时，运用GM(1,1)模型的跳变函数进行预测：

7)当预测日期不是预测跳变日期点时，运用线性回归函数Y(X)=a+bX进行预测。其中，Y(X)为回归预测函数;X为预测日期;a、b为待求系数。线性回归函数的确定，对任意相邻2个跳变点来说，前1个跳变点的上1个点与后1个跳变点的上1个点之间认为是线性关系。

3 实例分析

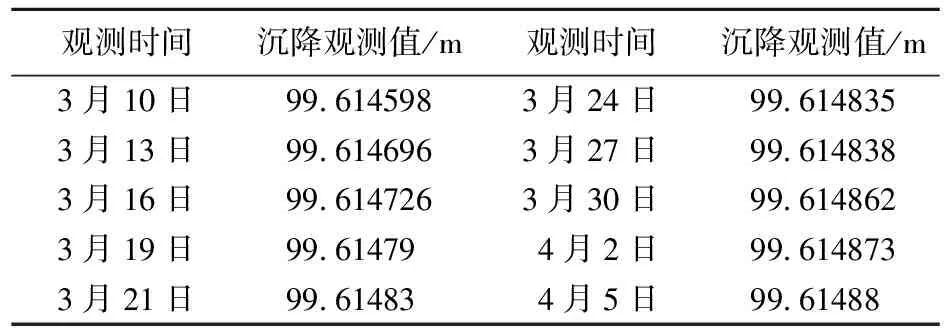
表1 Z4点沉降监测数据

以益阳市中心医院怡和楼的监测点Z4的监测数据为例进行建模分析，其中，观测时间以天为单位，且为等时间间隔观测序列，选用10期沉降观测值用于建立相应模型并进行预测精度对比。

3.1相关模型的建立

以上述数据作为原始序列，用Matlab软件编程求得参数a和b，得到各种模型的时间响应式如下。

1)GM(1,1)模型:

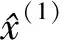
2)序列算子作用下的GM(1,1)模型:

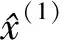
图1 沉降观测值曲线图

3)GM(1,1)与线性回归组合模型测点3、4、6和8为跳变点，而对应的测点1、2、5、7、9和10为非跳变点(见图1)，对跳变点建立GM(1,1)模型，得到跳变预测模型：

对非跳变点建立一元线性回归模型，通过拟合得到线性预测方程表达式：

Y=99.614622+0.000029X

3.2预测结果分析

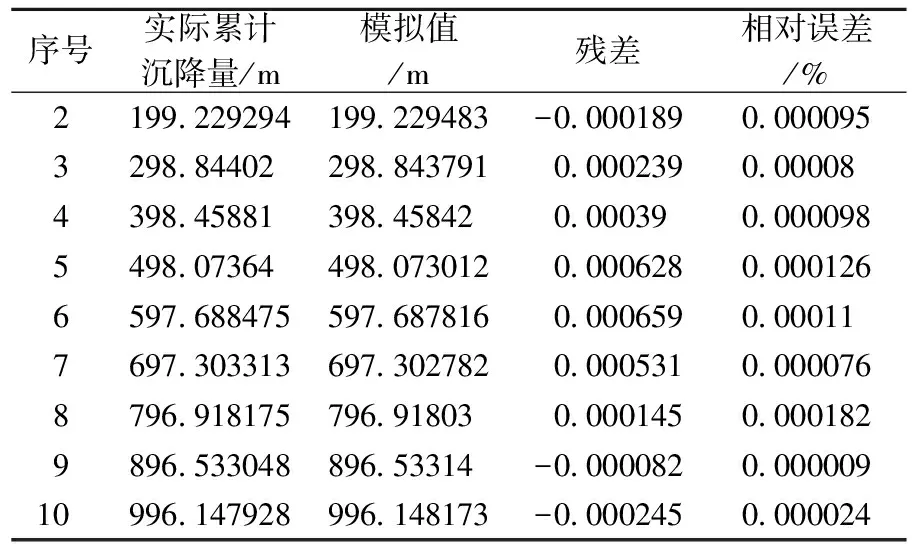
表2 GM(1,1)模型误差检验

对实际累计沉降量进行模拟，误差检验结果如表2、3、4所示。GM(1,1)模型、序列算子作用下的GM(1,1)模型以及GM(1,1)与线性回归组合模型的平均相对误差分别为0.00008889%、0.00003947%和0.00005309%，由此可以看出，改进的GM(1,1)模型预测精度均要优与传统的GM(1,1)模型。这是因为传统GM(1,1)模型是有偏差的灰指数模型，在沉降观测的过程中，受到许多外界因素的影响，使得沉降监测的数据存在很大的随机性和不连续性；序列算子可增强或减弱原始数据序列的增长速度，使得原始数据序列的光滑度加强，从而提高预测的精度；线性回归组合预测模型采用跳变点和非跳变点对原始序列进行处理，保持了原始数据序列的变化趋势，因此预测值与实际观测值的变化趋势十分相符。

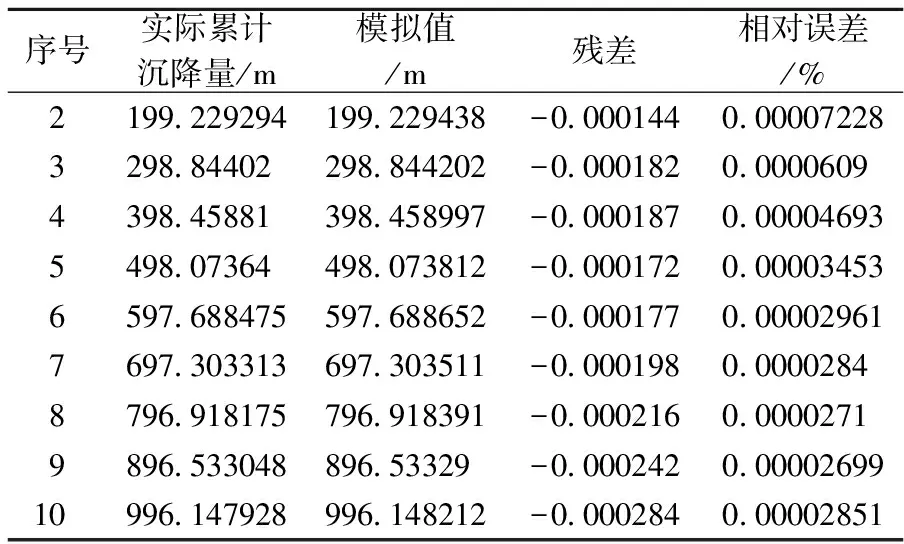
表3 序列算子作用下GM(1,1)模型误差检验

表4 GM(1,1)与线性回归组合模型误差检验

4 结语

传统GM(1,1)模型是有偏差的灰指数模型，存在着模型精度不高的问题，在沉降观测的过程中，受到许多外界因素的影响，使得沉降监测的数据存在很大的随机性和不连续性。针对沉降观测数据存在的缺陷，对3种模型进行了比较分析，其中运用序列算子作用的方法进行建模预测的拟合精度较高，线性回归组合预测模型则保持了原始数据序列的变化趋势，预测值与实际观测值的变化趋势十分符合。实例分析表明，改进后的GM(1,1)模型可以提高预测精度，将其运用于沉降监测系统后能满足工程实际要求。

[1]蒋泽中,陈天利.灰色理论在高层建筑沉降监测中的应用[J].建筑技术开发,2003，22(5)：38-41.

[2]邓聚龙.灰色系统基本方法[M].武汉:华中理工大学出版社,1987.

[3]徐辉,陈又星,费忠华.GM(1,1)模型适用域讨论及模型的改进[J].数学的实践与认识，2008，38(22)：134-139.

[4]刘思峰,党耀国，方志耕，等.灰色系统理论及其应用[M].北京:科学出版社,1999.

[5]许秀莉,罗键.GM(1,1)模型的改进方法及其应用[J].系统工程与电子技术，2002，24(4)：16-18.

[6]史雪荣,王钟羡.加权均值GM(1,1)模型及应用[J].江苏大学学报(自然科学版),2003，23(3)：89-91.

[7]鲍一丹,吴燕萍.基于GM(1,1)模型和线性回归的组合预测新方法[J].系统工程理论与实践，2004，12(3)：34-39.

10.3969/j.issn.1673-1409(N).2012.09.042

TU433

1673-1409(2012)09-N120-03

2012-06-26

广西开放实验室基金项目(桂科能1103108-12) 。