油罐车容积表的Matlab程序研发与应用
2012-11-22张志强中国石油天然气集团公司华北油田分公司第四采油厂河北廊坊065000
张志强,王 军,连 洁 (中国石油天然气集团公司华北油田分公司第四采油厂,河北 廊坊 065000)
油罐车容积表的Matlab程序研发与应用
张志强,王 军,连 洁 (中国石油天然气集团公司华北油田分公司第四采油厂,河北 廊坊 065000)
华北油田公司某采油厂作业大队目前共有各式罐车7辆,当时这些车辆为了满足油田的生产及实用性的考虑,交由改装厂改装。由于罐体缺乏液位深度-液体体积换算表,导致使用过程中存在诸多不便。通过对罐体尺寸进行精确测量,设计积分计算方法和Matlab编程,制作出较为准确的数据。经过实际应用后表明,此计算方法准确可靠。建议标准和非标准椭圆罐体截面2种规则罐体形状的改装罐车应用该程序制作液位换算表,以便准确测量罐内液体体积。
罐车;液位;容积;Matlab程序
华北油田某采油厂开发中后期开展精细化管理工作,对罐车计量工作提高了要求。标定罐车容积和“液位深度-液体体积”换算表可以辅助到一切罐车参与到的工作中去,具体体现在以下2个方面:罐车具体容积的确定有利于热洗等工作的顺利进行,利用这个表可以预先估算油井具体深度所需要的返水量,以便挑选合适的罐车,防止热洗时发生供水不足导致热洗中断从而延长油井热洗时间,影响生产;在单井拉油点拉油过程中,通过换算表可以得知罐车内精确的原油体积,防止盗窃,发挥油罐车作为计量器具的功用。下面,笔者Matlab程序制作液位换算表,以准确测量罐内液体体积。
1 罐体的测量和计算
1.1标准椭圆罐体截面

图1 对椭圆罐体进行移位处理示意图
适用于冀J5993X、 冀J5176X、 冀J4708X、冀J5179X、冀J5069X、冀J5069X共6辆罐车。为了方便测量, 定义a、b分别为“长轴”和“短轴”长,罐体长度为c。于是用于计算的椭圆方程变为:
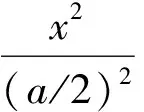
为了使所有积分区域变为正值方便积分计算[1],将标准椭圆方程向上移b/2的高度(见图1):
2个积分区域的面积为:
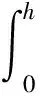
罐体现有液体的体积为:
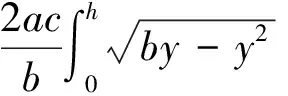
标准椭圆截面罐车液位计算的Matlab代码:
syms a b c h y;
a=input(’请输入长轴长:’);
b=input(’请输入短轴长:’);
c=input(’请输入罐体长:’);
h=input(’请输入液面高度:’);
f=sqrt(b*y-y.^2);f1=simple(int(f,y,0,h));
f2=(2*a*c/b)*f1;
ans=vpa(f2,6)
1.2非标准椭圆罐体截面
特殊截面罐体的积分计算适用于冀R2392X以及从华北运输公司租用的4辆相同型号的罐车。这种罐体截面可以看成是2个重叠的椭圆在垂直方向上拉开了距离L, 为了方便测量,将此截面的“高”和“宽”分别定义为b和a。由于罐体形状的复杂性,将积分区域,分为3个区域来保证计算精度[2](见图2中的1、2、3)。
3部分面积进行分段函数积分求解,对y求积分,分段积分结果如下:
这种截面的体积计算结果为3段:

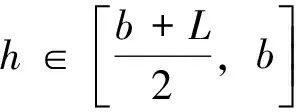

图2 非标准椭圆罐体 图3 非标准椭圆罐体液位示意图
用if-elseif-else语句进行简单的判断[3],分段积分得到特殊截面罐车液位(见图3)计算代码:
syms a b c L h y;
a=input(’请输入长轴长:’);
b=input(’请输入短轴长:’);
c=input(’请输入罐体长:’);
L=input(’请输入L长:’);
h=input(’请输入液面高度:’);
if 0<=h&h<=(b-L)/2;
v=(2*a*c/(b-L))*int(sqrt((b-L)*y-y.^2),0,h);
ans=vpa(v,6)
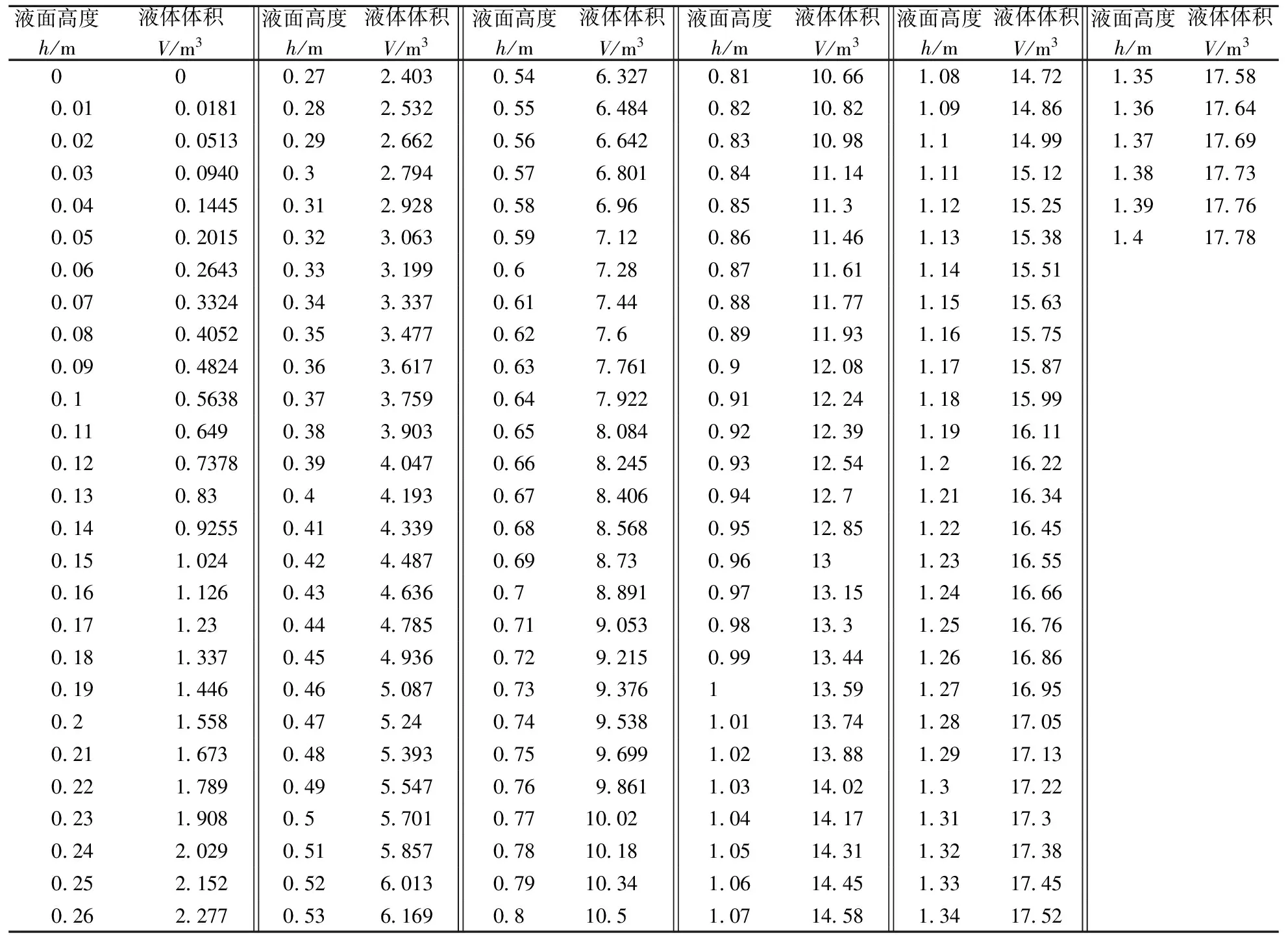
elseif (b-L)/2 v=pi*a*c*(b-L)/8+a*(h-(b-L)/2)*c; ans=vpa(v,6) else (b+L)/2 v=pi*a*c*(b-L)/8+a*c*L+(2*a*c/(b-L))*int(sqrt((b+L)*y-y.^2-b*L),(b+L)/2,h); ans=vpa(v,6) end 编写出以上2个程序后,要获得液体体积的精确数据[4],只需3步:判断罐车截面类型;将液位深度数据输入到对应的程序代码中;运行程序获得精确数据,得到结果。 笔者以冀J5993X(18m3罐车)为例[5],计算了罐车的液体体积,结果如表1所示。 表1 体积表(以冀J5993X,18m3罐车为例) 计算出来的体积表能够拓展应用到更加广阔的方面:如输油联合站、加油站等所有罐车应用广泛的单位,让这些为采油厂服务的罐车具备了计量功能,解决了十几年的遗留问题。这种计算方法基于精确测量和程序计算,不仅节省时间,而且准确度高,容易实施,效果显著。计算出来的换算表可以任意设定精确度值,从而打印制表分发给罐车司机和各采油单位使用。 [1]薛定宇,陈阳泉.高等应用数学问题中的Matlab求解[M].第3版.北京:清华大学出版社,2008:47-80. [2]卢志权.铁路罐车计量误差及原因浅析[J].中国计量,2008(2):1-2. [3]赵小伟,徐刚,刘冀.使用定积分方法求解倾斜偏转卧式储油罐容积[J].油气储运,2012(3):100-102. [4]王宇.浅谈椭圆形端板罐车容积表的选择[J].铁道技术监督,1996(5):1-2. [5]张治恺.浅谈GL17沥青罐车容积表的处理方法[J].铁道标准化,1994(4):1-3. 10.3969/j.issn.1673-1409(N).2012.09.028 TE972 A 1673-1409(2012)09-N078-03 2012-06-12 张志强(1983-),男,2006年大学毕业,硕士,助理工程师,现主要从事地质工程方面的研究工作。 [编辑] 洪云飞2 应 用