高阶方向导数与乘积函数高阶导数的形式一致性探讨

张 骞 (陇东学院数学与统计学院，甘肃 庆阳 745000)

高阶方向导数与乘积函数高阶导数的形式一致性探讨

张 骞 (陇东学院数学与统计学院，甘肃 庆阳 745000)

推导了乘积函数的高阶导数和高阶方向导数的计算，并对两者进行比较，得出了其形式一致性的结果。

高阶导数；方向导数；一致性

导数、高阶导数、高阶偏导数、方向导数[1-4]是微积分理论中很重要的知识点，其中高阶导数的计算是一个难点，而对于高阶方向导数更少涉及。为此，笔者主要给出了乘积函数高阶导数的计算和高阶方向导数的概念及计算，得到两者的规律以及简单表示方法。

1 乘积函数的高阶导数

1.1f(x)g(x)的高阶导数

设f(x)与g(x)分别为任意阶可导函数，f(x)与g(x)可视为f(x)与g(x)的零阶导数f(0)(x)与g(0)(x)，则：

[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x)

[f(x)g(x)]″=f″(x)g(x)+2f′(x)g′(x)+f(x)g″(x)

[f(x)g(x)]‴=f‴(x)g(x)+3f″(x)g′(x)+3f′(x)g″(x)+f(x)g‴(x)

利用数学归纳法可以得到f(x)g(x)的n阶导数：

其形式与二项式(a+b)n的展开式相似，于是乘积函数f(x)g(x)的n阶导数可以简单表示为[f(x)+g(x)](n)。

1.2f(x)g(x)h(x)的高阶导数

设f(x)、g(x)与h(x)分别为任意阶可导函数，则:

(fgh)′=f′gh+fg′h+fgh′

(fgh)″=f″gh+fg″h+fgh″+2f′g′h+2f′gh′+2fg′h′

(fgh)‴=f‴gh+fg‴h+fgh‴+3f″g′h+3f′g″h+3f″gh′+3f′gh″+3fg″h′+3fg′h″+6f′g′h′

同理，利用数学归纳法可知f(x)g(x)h(x)的n阶导数：

与三项式(a+b+c)n的展开式相似，于是乘积函数f(x)g(x)h(x)的n阶导数可以简单表示为[f(x)+g(x)+h(x)](n)。

1.3f1f2…fk的高阶导数

依次类推可知乘积函数f1f2…fk的n阶导数与(a1+a2+…+a3)n的展开式相似，于是乘积函数f1f2…fk的n阶导数可以简单表示为[f1+f2+…+f3](n)。

2 高阶方向导数

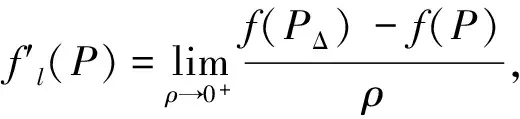
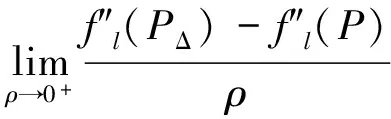
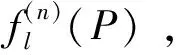
设函数f(x,y)在任意点P(x,y)存在所有二阶连续偏导数，则f沿任一方向l的二阶方向导数都存在，且：

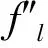
式中，cosα，cosβ为方向l的方向余弦。可简单表示为：

依次有：

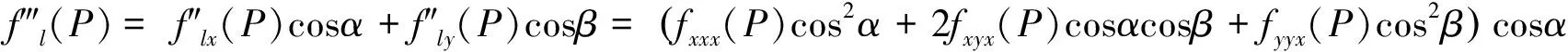
+(fxxy(P)cos2α+2fxyy(P)cosαcosβ+fyyy(P)cos2β)cosβ

=fxxx(P)cos3α+3fxxy(P)cos2αcosβ+3fxyycosαcos2β+fyyy(P)cos3β

可表示为：

若f(x,y)存在n阶连续偏导数，则：

推广到三元函数的n阶方向导数：

式中， cosα，cosβ, cosγ为方向l的方向余弦。

对于任意多元函数，也有：

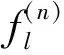
式中， cosα1,cosα2,…,cosαk为方向l的方向余弦。

3 形式一致性

通过上述2类高阶导数形式的比较，可以得到：

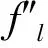
2)[f(x)g(x)]‴与f‴l(x,y)均相似于二项式(a+b)3的展开式。

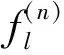
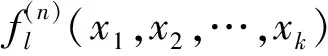
可见，乘积函数的高阶导数与高阶方向导数具有形式一致性。

[1]华东师范大学数学系. 数学分析(上册)[M] .第3版.北京：高等教育出版社，2001.

[2] 华东师范大学数学系. 数学分析(下册)[M] .第3版.北京：高等教育出版社，2001.

[3] 刘玉琏.数学分析讲义(上册)[M].第4版.北京：高等教育出版社，2003.

[4] 刘玉琏.数学分析讲义(下册)[M].第4版.北京：高等教育出版社，2003.

[5] 张骞. 高阶方向导数与多元Taylor定理的简单形式[J]. 菏泽学院学报，2011(2)：11-13.

10.3969/j.issn.1673-1409(N).2012.09.002

O175.15

A

1673-1409(2012)09-N004-02

2012-06-16

张骞(1976-)，男， 2000年大学毕业，硕士，副教授，现主要从事非线性泛函分析和函数论方面的教学与研究工作。

[编辑] 洪云飞