改进的储量参数碾平算法研究
2012-11-21张豆娟陈存元苏成义宋新娥王永刚李英英秦东风翟晓英韩连滨赫鹏飞王一楠
张豆娟 陈存元 耿 斌,苏成义,宋新娥 王永刚,李英英,方 丽 秦东风,翟晓英,闫 华,韩连滨 赫鹏飞,王一楠
(中石化胜利油田分公司地质科学研究院,山东 东营 257015) (中石化胜利石油管理局地质录井公司,山东 东营 257000) (中石化胜利油田分公司地质科学研究院,山东 东营 257015) (中石化国际石油勘探开发有限公司,北京 100029)
改进的储量参数碾平算法研究
张豆娟 陈存元 耿 斌,苏成义,宋新娥 王永刚,李英英,方 丽 秦东风,翟晓英,闫 华,韩连滨 赫鹏飞,王一楠
(中石化胜利油田分公司地质科学研究院,山东 东营 257015) (中石化胜利石油管理局地质录井公司,山东 东营 257000) (中石化胜利油田分公司地质科学研究院,山东 东营 257015) (中石化国际石油勘探开发有限公司,北京 100029)
为了消除目前储量参数碾平算法中的系统误差和降低进位误差,对原有的储量参数碾平算法进行了改进。采用地面脱气原油体积、质量、溶解气约束方法碾平储量合计单元各项参数,从而有效消除储量参数碾平中的单项系统误差;将各碾平参数值在各自变化范围内按照最小单位步长先离散化,再采用全排列组合法优选出使体积、质量、溶解气储量相对误差平方和达到最小的一组参数,该组参数即为合计项的最优储量参数碾平项选择。经过检验,利用该方法能够降低进位误差。
储量参数;改进碾平算法;地面脱气原油体积;地面脱气原油质量;溶解气;系统误差;进位误差
在石油勘探开发及储量计算中,通常在用容积法计算某个油田区块各个计算单元储量后需要碾平一个合计项的各参数平均值,这样在油田各项评价中可以对各油田之间的储量参数或一个油田不同时期的储量参数进行对比分析。由于一个油田的储量一般是多个层位、区块储量的累加,而大油田的储量计算单元有时达数百个之多,因而利用权衡法算出的各参数平均值相乘得出的储量与各个计算单元储量累计有一定误差[1]。当储量合计单元各参数的乘积不等于各储量计算单元的储量之和时,可以在合计计算单元的各参数之间平差,目前误差平差方法的缺失导致必然同时存在一部分进位误差。原计算方法的缺陷集中反映在由储量合计算单元各碾平参数的乘积算出的储量不等于各储量计算单元的储量之和。为了消除目前储量参数碾平算法中的系统误差和降低进位误差,笔者对原有储量参数碾平算法进行了改进研究。
1 消除系统误差
1.1基本原理
从生产实际要求出发,碾平参数的目的是为了求取众多计算单元储量累加后,最能代表这些储量参数的平均值,同时由各碾平参数的乘积计算出的储量与各计算单元的累加储量误差最小,即储量参数碾平后计算出的体积、质量、溶解气误差最小。改进的储量参数碾平算法的核心是通过使由储量合计算单元各碾平参数的乘积计算出的地质储量与各储量计算单元的地质储量之和(体积储量、质量储量、溶解气储量)相等,从而达到消除系统误差的目的。
1)累加体积储量 一个区块各计算单元的累加体积储量由下式计算得到:
(1)
式中,N为一个区块各计算单元的累加体积储量,104m3;n为区块中的计算单元数;Ai为区块中第i个计算单元的含油面积,km2;hi为各计算单元有效厚度,m;Φi为各计算单元有效孔隙度,%;Soi为各计算单元原始含油饱和度,%;Boi为各计算单元原油体积系数。
2)累加质量储量 一个区块各计算单元的累加质量储量由下式计算得到:
(2)
式中,Nz为区块各计算单元的累加质量储量,104t;ρoi为各计算单元地面原油密度,g/cm3。
3)累加溶解气储量 一个区块各计算单元的累加溶解气储量由下式计算得到:
(3)
式中,Gs为1个区块各计算单元的累加溶解气储量,108m3;Rsi为各计算单元的溶解气油比。
4)体积储量 体积储量Na(要求Na与N相等)由下式计算得到:
(4)

5)质量储量 质量储量Nza(要求Nza与Nz相等)由下式计算得到:
(5)
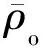
6)溶解气储量 溶解气储量Gsa(要求Gsa与Gs相等)由下式计算得到:
(6)
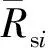
1.2具体步骤
步1 合计单元含油面积取各计算单元面积Ai的叠合含油面积A。
步2 计算合计单元碾平地面原油密度和溶解气油比:

步3 分别采用地面脱气原油体积、质量、溶解气约束法碾平有效孔隙度、原始含油饱和度、原油体积系数。
①采用地面脱气原油体积、质量、溶解气约束法碾平有效孔隙度:

②分别采用地面脱气原油体积、质量、溶解气约束法碾平原始含油饱和度:
③分别采用地面脱气原油体积、质量、溶解气约束法碾平原油体积系数:
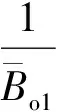
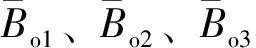
步4 由于有效厚度仅保留1位小数,其进位误差对储量计算结果影响较大,同时由于纵向上各计算单元含油面积可能会叠合而造成合计单元厚度增大,因而在碾平了其他储量参数后,应依据各计算单元累加体积、质量、溶解气储量反算碾平有效厚度:
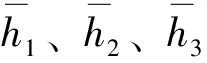
樊101区块沙三中亚段储量表如表1所示。根据表1利用改进算法与原有算法分别进行计算,在全保留小数位数时,与原有算法相比,改进算法可以消除单项系统误差(见表2)。

表1 樊101区块沙三中地质储量表

表2 改进后的算法与原有算法在樊101区块沙三中亚段的应用对比
2 降低进位误差
2.1基本原理
由于储量计算规范要求各参数保留一定小数位数(含油面积保留2位小数,地面脱气原油密度保留3位小数,原始溶解气油比取整,有效孔隙度保留1位小数,原始含油饱和度保留1位小数,原油体积系数保留3位小数,有效厚度保留1位小数),这样必然导致进位误差存在。为了尽可能合理地考虑误差程度,选用相对误差来约束。首先将这些参数在它们的变化范围内按照最小单位步长离散化,然后全排列组合优选一组参数使体积、质量、溶解气储量相对误差平方和达到最小,这样由该组参数计算出来的体积储量、质量储量和溶解气储量的相对误差较小,从而达到降低进位误差的目的。
2.2具体步骤
步1 合计单元含油面积取各计算单元面积Ai的叠合含油面积A。

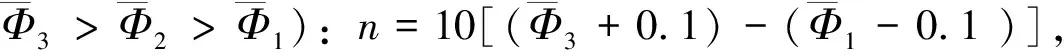
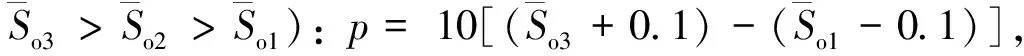

2.3应用效果
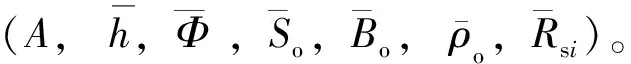
埕北15井区储量表如表3所示。根据表3利用改进算法与原有算法分别进行计算,结果如表4所示。由表4可知,改进算法可以显著降低进位误差。

表3 埕北15井区储量表

表4 改进算法与原有算法在埕北15井区的应用对比
3 结论与建议
1)分别采用地面脱气原油体积、质量、溶解气约束方法碾平储量合计单元各参数,可以有效消除储量参数碾平中的单项系统误差。
2)将各碾平参数值在各自变化范围内按照最小单位步长先离散化,再采用全排列组合法优选出使体积、质量、溶解气储量相对误差平方和达到最小的一组参数,该组参数即为合计项的最优储量参数碾平项选择。经过检验,利用该方法能够降低进位误差。
3)在实际应用时发现用溶解气体积约束方法碾平出的各项储量参数与体积、质量约束方法所计算的参数很不相同,这样会使参数动态范围变化很大,最终增加运算量而计算精度提高不大。因此,建议仅考虑体积、质量约束来碾平合计单元参数,而溶解气油比可采用溶解气储量除以体积储量的简便方法来获得。
[1]杨通佑,范尚炯,陈元千,等. 石油及天然气储量计算方法[M]. 北京:石油工业出版社,1990.
10.3969/j.issn.1673-1409(N).2012.07.020
TE328
A
1673-1409(2012)07-N061-04
2012-04-13
张豆娟(1979-),女,2004年大学毕业,硕士,工程师,现主要从事油气勘探开发及储量管理方面的研究工作。
[编辑] 李启栋
