高速非达西渗流压力动态分析

李林凯，姜瑞忠

(中国石油大学(华东)石油工程学院，山东 青岛 266555)

魏朋朋

(中石油大港油田分公司勘探开发研究院，天津 300280)

李 红

(中海油能源发展监督监理技术公司，天津 300452)

高速非达西渗流压力动态分析

李林凯，姜瑞忠

(中国石油大学(华东)石油工程学院，山东 青岛 266555)

魏朋朋

(中石油大港油田分公司勘探开发研究院，天津 300280)

李 红

(中海油能源发展监督监理技术公司，天津 300452)

当流体的渗流速度较大时，呈现出高速非达西渗流，为准确地描述其渗流规律，基于高速非达西渗流新模型，建立了考虑井筒储存和表皮系数的试井模型，并采用有限差分求解。结果表明，考虑高速非达西后，压力曲线上移，压力导数曲线驼峰高度增加并后移，水平段出现的时间延迟。与Forchheimer模型相比，新模型的上升幅度要小。Kmr和τD是影响曲线特征的重要参数，决定了曲线驼峰的高度和位置。随着Kmr减小，τD增大，压力曲线上移幅度增大，压力导数曲线驼峰高度增加幅度增大。

新模型；高速非达西；数值解；试井；压力恢复

室内试验和开发实践表明，当流体的渗流速度较大时，呈现出高速非达西渗流，而达西定律无法准确地描述其渗流规律。为此Forchheimer[1]对达西定律进行了修正，提出以下模型(简称F模型)来描述高速非达西渗流：

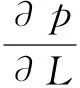
(1)

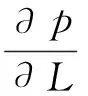
许多学者[2-8]基于该模型进行了高速非达西渗流的试井分析。但是，即使在Forchheimer公布的实验数据中，也有一些数据点不能用速度的二次方程来描述。为此，笔者基于高速非达西渗流新模型，讨论了压力降落及压力恢复试井的情况，为高速非达西试井提供理论依据。

1 高速非达西渗流新模型

Barree等[9]认为在流速相当高的条件下，流体渗流存在最小渗透率，达西定律和Forchheimer方程都不能准确地描述其渗流规律，在大量试验的基础上提出了渗流新模型(简称BC模型)：

(2)

式中，Kmr=Kmin/K，Kmin为最小渗透率，μm2；τ为常数，100/cm;Kmr是最小渗透率与渗透率之比。

当Kmr=0时，该模型简化为Forchheimer模型。当Kmr=0，τ→∞时，该模型简化为达西模型。Kmr、τ可以通过试验数据的非线性拟合获得。与F模型相比，该模型能更准确地的描述试验数据。

2 试井模型

假设油井定量生产，且地层流体符合高速非达西渗透新模型，其他假设条件与常规试井一致。

引入有效井径的概念，定义如下无因次量：

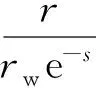
式中，rD为无因次井径；r为地层某点离井筒中心的距离，cm；tD为无因次时间；pD为无因次压力；pi为原始地层压力，0.1MPa；p为地层某点的压力，0.1MPa；CD为无因次存储系数；τD为无因次岩性常数；rw为井筒半径，cm;q为地面产量；B为体积系数；t为时间，s；s为表皮系数；φ为孔隙度；Ct为裂缝综合压缩系数，10MPa；h为储层高度，cm；C为存储量系数,10cm3/MPa。

由高速非达西渗流新模型、状态方程和连续性方程，得到如下无因次数学模型：

(3)

初始条件：

pD(rD,tD=0)=0

(4)

内边界条件：

(5)

封闭外边界：

(6)

定压内边界：

pD|rD=reD=0

(7)

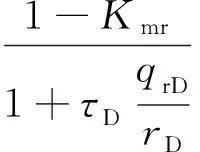
式(3)～(7)组成了高速非达西渗流的试井模型，该模型是非线性偏微分方程，采用有限差分数值求解。

3 数值求解

3.1 差分离散

空间步长i选取等比数列，取空间坐标变换rD=ex，将不等距径向坐标转换为等距直角坐标，时间步长n取对数数列[10]。

对试井模型采用隐式中心差分得：

(8)

内边界处：

(9)

封闭外边界处(i=m)：

(10)

定压边界处(i=m-1)：

(11)

式中，Δx=lnreD/(m-1)，Mi=e2(i-1)Δxe-2sΔx2/ΔtD，m为网格总数。

式(8)～(11)组成该试井模型的差分格式。

3.2 高速非达西校正系数δ的计算

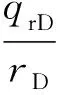
将BC模型无因次化，得：

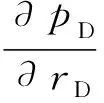
(12)

整理得：

(13)

解上述一元二次方程得：

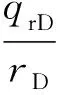
(14)

由此确定δ值。

3.3 试井模型的求解

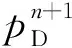
4 结果分析

图1所示为不同模型的高速非达西校正因子与雷诺数的曲线。由图1可知，达西模型的校正因子是1，F模型和BC模型的校正系数随着雷诺数的增大逐渐减小，但BC模型的校正系数最终趋于常数，这主要是因为考虑了最小渗透率的缘故。从图1可以看出，Re≈0.1可以作为达西与高速非达西渗流的分界点，这与文献[12]的结论基本一致。

图2所示为不同模型的试井曲线，其中CDe2x=100。由图2可以看出，考虑高速非达西渗流后，压力曲线上移，在径向流动阶段曲线基本保持平行；压力导数曲线驼峰高度增加并后移，水平段出现的时间延迟，即径向流动阶段开始的时间延迟，随着时间的增大，压力导数曲线趋向0.5水平线。与F模型相比，BC模型的增加幅度要小。

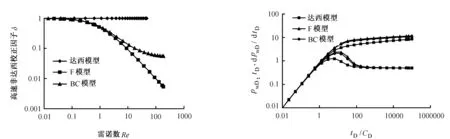
注：达西模型(Kmr=1)；F模型(Kmr=0，τD=3)；BC模型(Kmr=0.1，τD=3) 图1 不同模型的高速非达西校正因子与雷诺数的曲线 图2 不同模型的试井曲线

图3所示为Kmr和τD对试井曲线的影响，其中，CDe2s=100。从图3可知，Kmr和τD是影响曲线特征的重要参数，决定了曲线驼峰的高度和位置。随着Kmr减小，τD增大，压力曲线上移幅度增大，压力导数曲线驼峰高度增加幅度增大。

图4所示为定压边界对试井曲线的影响，其中，CDe2s=100，ReD=5000。由图4可知，当压力波传到定压边界时，无论参数Kmr和τD取值如何，压力曲线趋于水平，压力导数曲线下弯。

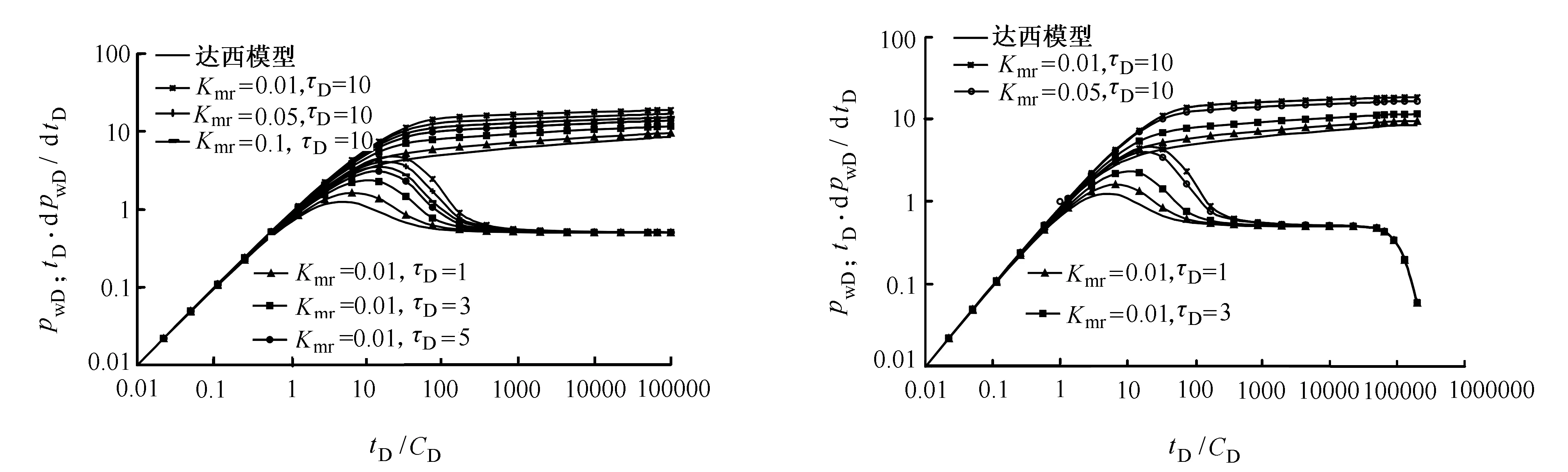
图3 Kmr和τD对试井曲线的影响 图4 定压边界对试井曲线的影响

图5所示为封闭边界对试井曲线的影响，其中 ，CDe2s=1000,ReD=15000。由图5可知，当压力波传到封闭边界时，压力和压力导数曲线上翘，Kmr和τD的取值不影响边界曲线的形态。

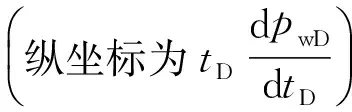
图6 所示为BC模型压力降落和压力恢复试井曲线对比图，其中，CDe2s=10000，Kmr=0.01，τD=5。由图6可知，BC模型压力降落试井和压力恢复试井的压力导数曲线不像达西模型那样重合。所以，不能像达西模型那样简单地用压力降落试井曲线拟合压力恢复试井数据，否则不能取得理想的拟合结果。

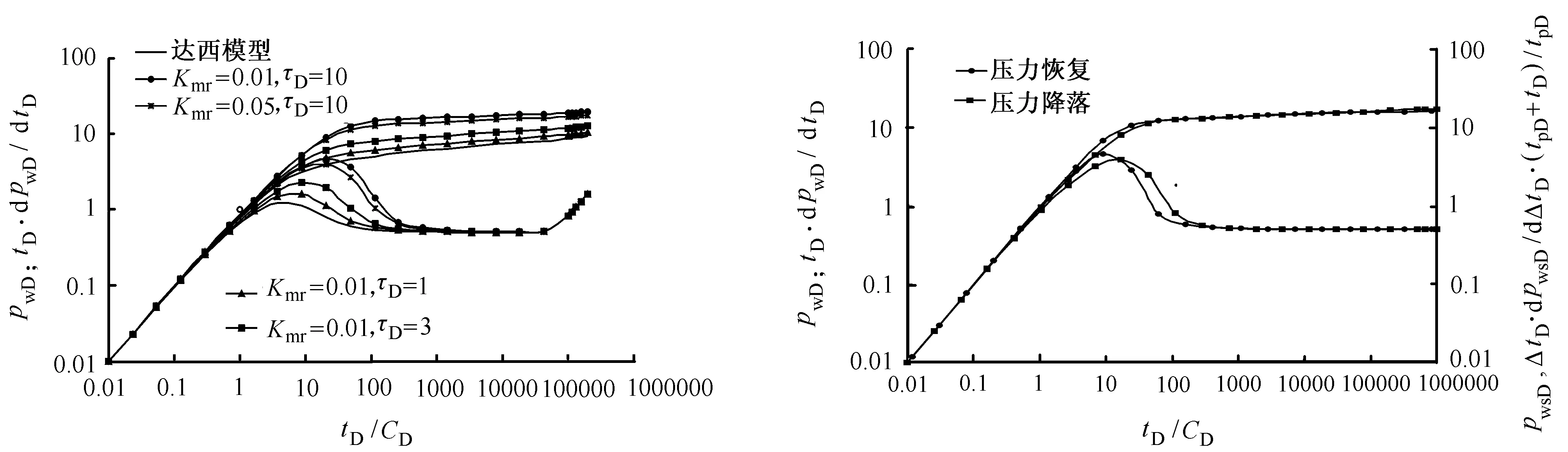
图5 封闭边界对试井曲线的影响 图6 BC模型压力降落和压力恢复试井曲线对比图

BC模型和达西模型压力恢复曲线对比图如图7所示。由图7可知，BC模型压力恢复的压力曲线与达西模型基本重合。当油井以恒定产量生产时，BC模型所预测的压降比达西模型要大。但当关井时，2个模型的压力恢复曲线重合，说明压力恢复时由于流速较低，高速非线性渗流不明显，呈现出达西渗流的特点。

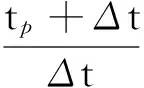
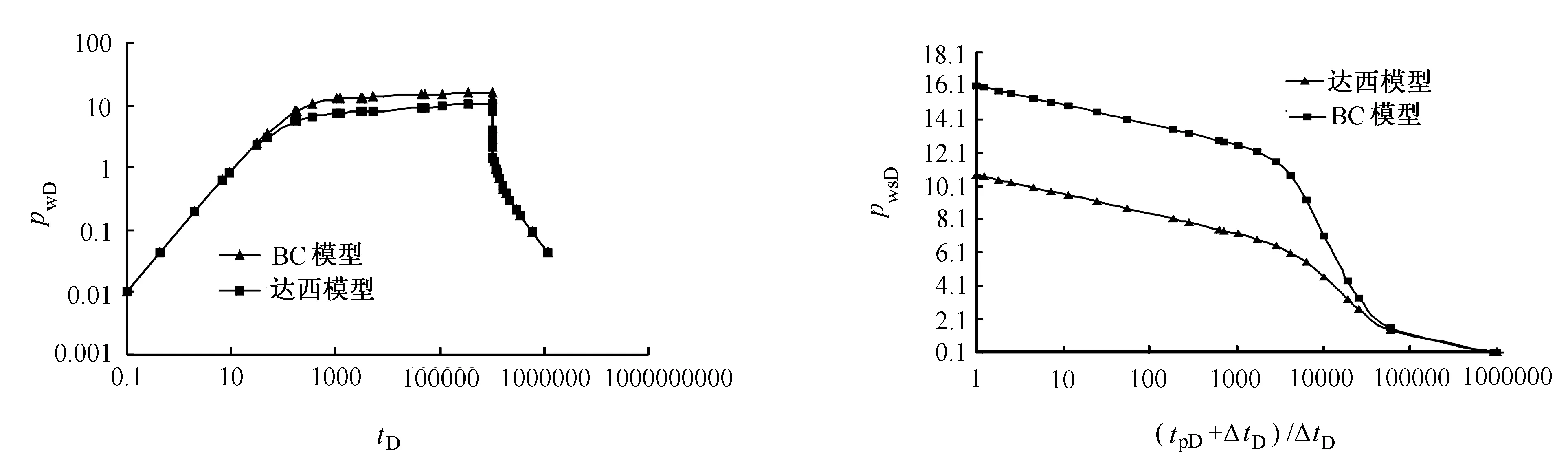
图7 BC模型和达西模型压力恢复曲线对比图 图8 无因次Horner曲线

5 结 论

基于高速非达西渗流新模型建立试井解释模型并采用数值方法求解，对比分析了达西模型、Forchheimer模型和渗流新模型压力响应曲线，讨论了非线性特征参数Kmr，τD以及边界条件对试井曲线的影响，阐述了高速非达西渗流压力降落试井和压力恢复试井的不同。研究发现，Kmr和τD是影响曲线特征的重要参数，决定了曲线驼峰的高度和位置。随着Kmr减小，τD增大，压力曲线上移幅度增大，压力导数曲线驼峰高度增加幅度增大。

[1]J·贝尔.多孔介质流体动力学[M]. 李竞生 译.北京：中国建筑工业出版社，1983.

[2] 张黔川，吕涛，吕劲.气藏水平井非达西流动二项式产能试井公式[J].天然气工业，2004，24(10)：83-85.

[3] 张烈辉，朱水桥，王坤，等.高速气体非达西渗流数学模型[J].新疆石油地质，2004，25(2)：165-167.

[4] 张德志，王子胜，战艾婷.高速非达西渗流时三重介质油藏的压力响应[J].油气地质与采收率，2009，16(1)：97-104.

[5] 崔传智，赵晓燕，苏玉亮.真实气体高速非达西流的单井数值模拟[J].辽宁工程技术大学学报(自然科学版)，2009,28(增)：61-63.

[6] 马婧，程世清.高速非达西气井渗流模型及压力曲线特征[J].石油钻探技术，2009，37(4)：28-31.

[7] 赵明跃，王新海，雷霆，等.高速非达西渗流井底压力响应特征研究[J].油气井测试，2001，10(5)：1-3.

[8] 赵晓燕，姚军，崔传智，等.考虑真实气体PVT动态的高速非达西渗流模型[J].石油钻探技术，2009，37(2)：78-81.

[9] Barree L,Conway R. Beyond Beta Factors: A Complete Model for Darcy, Forchheimer and Trans-Forchheimer Flow in Porous Media[J]. SPE 89325，1998.

[10] 李淑霞，谷建伟.油藏数值模拟基础[M].东营：中国石油大学出版社，2009.

[11] 张建国，雷光伦，张艳玉.油气层渗流力学[M].东营：中国石油大学出版社，2006.

[12] 刘能强.实用现代试井解释方法[M].北京：石油大学出版社，1996.

[编辑] 李启栋

10.3969/j.issn.1673-1409(N).2012.10.029

TE312

A

1673-1409(2012)10-N093-05