基于最大熵原理的广义灰色关联模型及应用

黎延海

(陕西理工学院数学系，陕西 汉中 723000)

基于最大熵原理的广义灰色关联模型及应用

黎延海

(陕西理工学院数学系，陕西 汉中 723000)

通过对现有灰色关联模型的研究，以序列相邻采样点间的面积作为计算关联系数的依据，并基于离差最大化和最大熵原理，建立了计算关联系数权重的数学模型，得到加权灰色关联度。将该模型应用于工程招标问题中，结果表明该模型有较高的可靠性和应用性。

灰色关联分析；离差最大化；最大熵原理；工程招标

灰色关联分析是灰色系统理论[1-2]的重要组成部分，是研究系统内部因素之间关联程度的一种数学模型。灰色系统理论发展至今，已有许多成熟的关联度模型，如邓氏关联度、广义灰关联度、绝对关联度、T型关联度、斜率关联度等，这些模型分别按照基于距离、基于斜率和基于有向面积的相似度量原理来进行分析。邓氏关联度容易受到数据极值和采样数据质量的影响，广义灰色关联度在2曲线上下波动时所得结果与定性分析不一致[3-4]，并且将灰色关联系数做简单的算术平均来得到灰色关联度，会造成信息损失和局部点关联测度值控制整个灰色关联序[5-6]。为此，笔者采用2曲线相邻采样点间的面积作为灰色关联系数的计算依据，讨论了分辨系数的选取，基于离差最大化和最大熵原理[7-8]，建立加权系数的数学模型，得到了加权灰色关联度模型，并将改进的关联度模型应用于工程招标问题中。

1 基于最大熵原理的广义灰色关联度

1.1 改进的面积灰色关联系数

定义1设系统特征序列X和行为序列Xi分别为：

X={x(t1),x(t2),…,x(tn)}Xi={xi(t1),xi(t2),…,xi(tn)} (i=1,2,…,m)

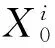
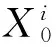
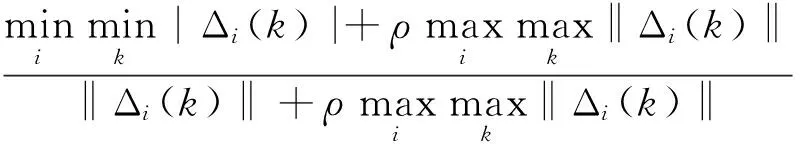
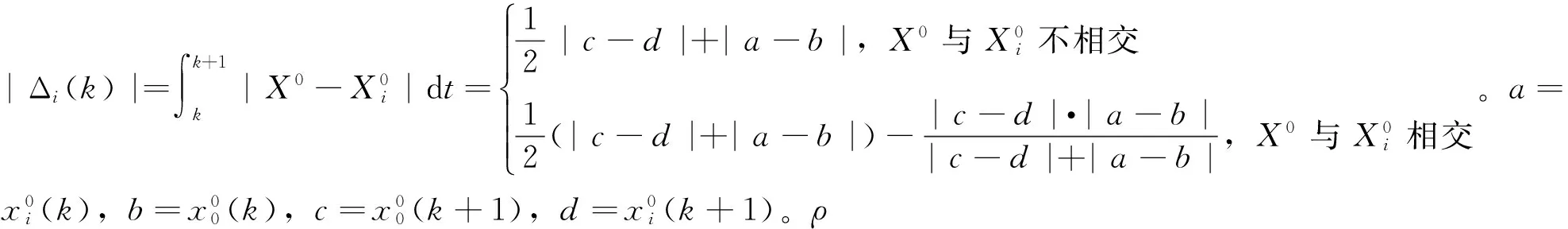
1.2 关联系数权重的优化模型

定义2[10-11]ξi={ξi(1),ξi(2),…,ξi(n-1)}为灰色关联系数序列，就其第k个分量，称：

为序列ξi与其他序列的离差。称：

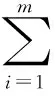
为所有序列与其他序列的总离差。

灰色关联系数反映了比较序列各点对主行为序列的影响。如果关联系数序列的第k个分量对所有序列而言无大的差异，则该分量对关联度的影响较小，该分量的权值就应该较小。反之，如果第k个分量使所有序列的关联度有较大的差异，则该分量的权值就应该取较大值。同时由于各分量的权重是一个随机变量，具有不确定性。为得到合理的权重，一方面应使所有序列分量对所有序列的总离差最大化，另一方面尽量消除各分量权重的不确定性，为达到上述2个目标，可建立如下的优化模型：

(1)

其中，0<μ<1，用来表示2个目标间的平衡系数，可根据实际问题预先给出。

定理1[8]模型(1)有唯一解，其解为：

1.3 加权关联度模型的建立

采用2曲线相邻采样点间的面积来计算灰色关联系数ξi，基于离差最大化和最大熵原理，求得关联系数的权重ωk，建立加权灰色关联度模型，即：

称为序列X与Xi的改进广义灰色关联度。

1.4 改进关联度的性质

显然，改进的关联度模型可以很好的度量曲线的相似性，并满足灰色关联4公理，即规范性、整体性、偶对称性和接近性。

2 应 用

某市一建筑工程采用工程量清单计价模式进行招标，有4家投标单位通过了资格预审。各投标单位的评价指标值见表1。其中工程质量保证体系、近5年工程质量情况和施工组织设计这3项指标值是通过专家打分得到。

表1 投标单位标书评价指标值

设X={892.52,80,167,87,80,90,17.2}作为参考序列，取平衡系数μ=0.5，得到关联系数权重向量ω=(0.154952,0.123027,0.041297,0.110691,0.458945)，最后得到4个方案与理想方案的灰色关联度为r1=0.79007，r2=0.502046,r3=0.57794，r4=0.669945，则方案排序为：方案1、方案4、方案3和方案2，所得结果与文献[12]结果一致，证明了方法的可靠性。

3 结 语

以改进的广义灰色关联度为基础，利用优化理论和最大熵原理，对关联系数加权平均计算灰色关联度，综合考虑了整体性对灰色关联度的影响，讨论了分辨系数的选取，能够有效控制关联系数的波动性，解决了局部点控制关联序的问题，并在序列波动和存在极值干扰时仍具有较高可靠性。将该模型应用于工程招标问题中，通过比较分析，所得评价结果合理，与定性分析相一致，证明了该模型的实用性和有效性。

[1]邓聚龙.灰理论基础[M].武汉：华中科技大学出版社，2002.

[2]李孜军.1992～2002年我国灰色系统理论应用研究进展[J].系统工程，2003，21(5)：8-12.

[3]王靖程，诸文智，张彦斌.基于面积的改进灰关联度算法[J].系统工程与电子技术，2010，32(4)：777-779.

[4]魏丽，陈丽宇.关于一类新的广义灰色关联度[J].宁夏大学学报(自然科学版)，2007，28(1)：22-24.

[5]王正新，党耀国，曹明霞.基于灰熵优化的加权灰色关联度[J].系统工程与电子技术，2010，32(4)：774-776.

[6]马引弟.模糊层次分析法在优秀企业家评定中的应用[J].产业与科技论坛，2009(4)：147-148.

[7]汪泽焱.一种基于最大离差和熵的多指标赋权方法[J].解放军理工大学学报(自然科学版)，2002(6)：93-95.

[8]姜汐，迟国泰，严丽俊.基于最大熵原理的线性组合赋权方法[J].运筹与管理，2011，20(1)：53-59.

[9]东亚斌，段志善.灰色关联度分辨系数的一种新的确定方法[J].西安建筑科技大学学报(自然科学版)，2008，40(4)：589-592.

[10]陈华友.多属性决策中基于离差最大化的组合赋权方法[J].系统工程与电子技术，2004，26(2)：194-197.

[11]张国权，李文立，王明征.基于离差函数和联合熵的组合赋权方法[J].管理学报，2008，5(3)：376-380.

[12]王芳.层次-熵定权的灰色关联理论在工程评标中的应用[J].河南科技大学学报(自然科学版)，2010，32(8)：49-56.

[编辑] 洪云飞

10.3969/j.issn.1673-1409(N).2012.10.003

O223

A

1673-1409(2012)10-N008-02