因子分析在学生能力评价中的应用——以广东金融学院2008级信息与计算科学专业为例

周雪刚，孙丽英， 张泳梅

(广东金融学院应用数学系，广东 广州 510521)

因子分析在学生能力评价中的应用
——以广东金融学院2008级信息与计算科学专业为例

周雪刚，孙丽英， 张泳梅

(广东金融学院应用数学系，广东 广州 510521)

运用因子分析法对广东金融学院2008级信息与计算科学专业学生进行了综合能力评价，所得到的评价结果可为学生自身的发展和教学策略的选择与实施提供科学依据和参考价值。

因子分析;能力评价; 学生成绩

信息与计算科学专业是数学、计算机科学与信息工程等学科相互渗透与交叉的专业，远远超出数学传统专业的范围，对学生的学习与能力提出了更高的要求，当然，也能培养学生更广泛的能力。如何更好的评价该专业学生通过大学4年的学习哪些能力方面得到了提高，以更好的指导学生根据自己的实力在毕业时寻找比较适合的工作，为教师在今后的教学工作中根据课程进行教学策略的选择与实施提供科学的依据和参考，为该专业的课程设置与教学改革指明方向。大学4年中能够反映学生学习情况与能力发展状况的主要是各门课程的考试成绩，而每门功课的培养目标和促进能力发展更是有多样性和差异性，因而在这样一个复杂多元的教学过程中, 仅仅通过单纯的总分或平均分来体现能力的提高显然过于片面和笼统,更不能体现出学生在各种能力间的优劣势。运用因子分析方法[1]建立综合评价指标和公共因子分析指标进行学生成绩评价和具体的优势、劣势的度量，一方面避免了单指标的片面性, 更重要的是在构造综合评价指标值时所涉及的权数都是通过数学变化产生, 其分析过程是从数据的内部结构出发, 最终获得学生学业成绩评价的信息, 克服了其他多指标法中存在的主观因素。同时, 通过设定公共因子可以解决传统方法中课程门数过多的弊端, 其能清晰地揭示影响学生成绩的主要原因, 对促进学生能力不断发展具有重要指导作用[2-5]。为此，笔者利用多元统计分析原理, 通过因子分析对广东金融学院2008级信息与计算科学专业2008年至2010年上半年各门课程成绩进行客观地分析，方便学生了解自己在各学科间的优势和劣势, 找出隐藏在成绩背后的个体能力，更好的认清自身的能力与发展方向❶。

1 数据来源

以广东金融学院应用数学系2008级信息与计算科学专业全体学生2008～2009学年、2009～2010学年、2010～2011学年3个学年49门课程的成绩作为原始数据, 运用SAS软件, 采用因子分析法对学生的成绩进行客观地分析。课程名称及编号如下(原始数据略):X1为思想道德修养与法律基础；X2为数学分析Ⅰ；X3为空间解析几何；X4为大学生健康教育；X5为大学英语视听说Ⅰ；X6为大学英语读写Ⅰ；X7为大学计算机Ⅰ；X8为高等代数Ⅰ；X9为大学语文；X10为数学分析Ⅱ ；X11为高等代数Ⅱ；X12为C语言程序设计；X13为C语言课程设计；X14为大学英语视听说Ⅱ；X15为大学英语读写Ⅱ；X16为毛泽东思想、邓小平理论和“三个代表”重要思想概论Ⅰ；X17为中国近现代史纲要；X18为普通物理；X19为数据结构；X20为马克思主义基本原理；X21为大学英语视听说Ⅲ；X22为大学英语读写Ⅲ；X23为数学分析Ⅲ；X24为概率论；X25为毛泽东思想、邓小平理论和“三个代表”重要思想概论Ⅱ；X26为大学英语视听说Ⅳ；X27为大学英语读写Ⅳ；X28为形势与政策；X29为近世代数；X30为运筹学；X31为复变函数；

X32为离散数学；X33为常微分方程；X34为廉洁修身；X35为数理统计；X36为算法设计与分析；X37为Matlab软件实验；X38为多元统计分析；X39为数据分析；X40为数学建模实践；X41为数学模型；X42为数值分析；X43为数值分析课程设计；X44为算法分析课程设计；X45为信息论基础与编码理论；X46为信息与编码课程设计；X47为大学生就业指导；X48为数据分析与SAS应用实验；X49为数据库原理与应用。

2 因子分析的主要结果

2.1 KMO检验

由于KMO的统计值0.81742056 大于0.6, 表明该研究适合进行因子分析。

2.2 基于主成分分析方法的因子分析

为了消除不同课程的影响，利用相关系数矩阵进行基于主成分分析方法的因子分析, 表1给出了计算其特征值及贡献率。根据累计贡献率, 取12个公共因子,反映了原始数据71.2%(>70%)的信息，把其作为反映原指标的信息量可以认为是有效的, 故可取出因子个数为12, 也就是说原来的49个门课程可以综合成12个公共因子：第1个公共因子解释的方差为16.208430，是12个公共因子中最大的，说明第1个公共因子在众公共因子中是最重要的，所占的比重也最大。表2给出12个公共因子所解释的方差，从中可以看出前4个公共因子所解释的方差最多，也最重要。

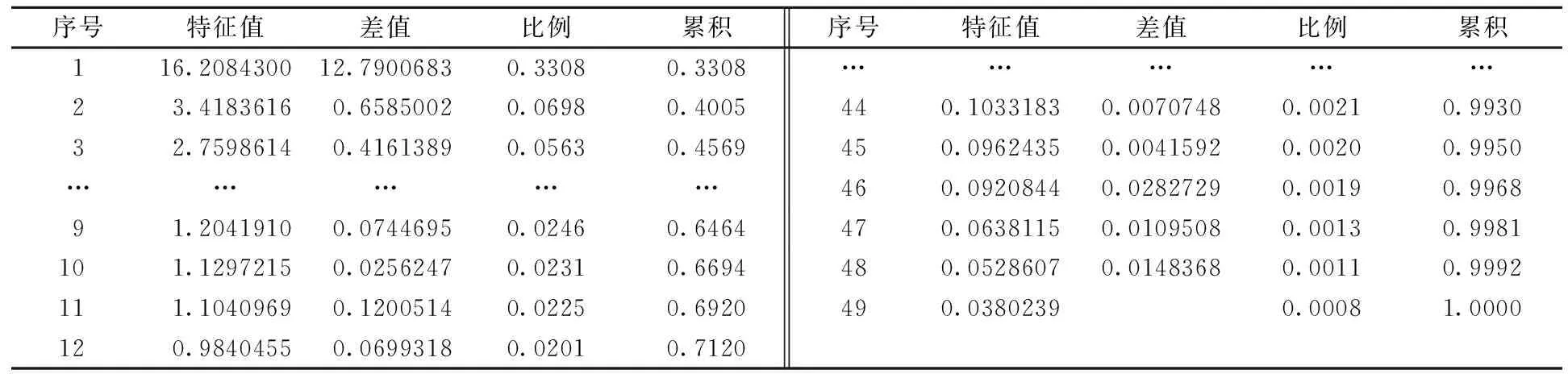
表1 相关阵的特征值

表2 12个公共因子解释的方差

2.3 未经过旋转的第1公共因子的因子载荷系数

未经过旋转的因子载荷矩阵中第1公共因子的因子载荷系数如下0.4265、0.5861、0.5400、0.3468、0.1827、0.5168、0.5015、0.5821、0.3733、0.7341、0.7945、0.5331、0.4076、0.4080、0.4959、 0.4462、0.5361、0.4839、0.8096、0.560、0.5650、0.6145、0.6919、 0.6616、 0.5499、0.6064、0.5625、0.5731、0.4461、0.8055、0.5808、0.2042、0.6809、0.3965、0.6831、0.7109、0.6023、0.5920、0.8330、0.6208、0.7922、0.6652、0.3540、0.5704、0.6577、0.5124、0.3391、0.4690、0.6535。说明其对49个变量中大部分变量都有较明显的影响作用，由此看出因子变量的含义还比较模糊，不利于对因子的实际背景进行合理的解释,因而需要进行因子旋转。

2.4 旋转后12个公共因子所解释的方差

表3是利用最大方差旋转法旋转后12个公共因子所解释的方差，从中可以看出前4个公共所解释的方差最大，也最重要。表4给出旋转后前5个公共因子的因子载荷矩阵, 旋转以后, 数据明显向0或1两极方向分化，这就大大有利于对公共因子进行解释。

1)计算能力因子 第1个公共因子中的载荷正向主要集中于X23、X24、X31、X33、X38、X41、X45，而负值都接近于0，说明第1个公共因子主要由这7个变量解释，而这些变量是关于数理方面的科目，称为计算能力因子。

2)抽象思维因子 第2个公共因子中的载荷正向主要集中于X2、X3、X8、X10、X11、X36、X41，X45，而负值都接近于0，说明第2个公共因子主要由这8个变量解释，这些变量都是与思维有关的科目，称为抽象思维因子。

3)表达能力因子 第3个公共因子中的载荷正向主要集中于X5、X6、X7、X14、X15、X21、X22、X27，而负都接近于0，而负值都接近于0，说明第3个公共因子主要由这8个变量解释，而这些变量是属于语言范畴的，称为表达能力因子。

4)信息处理因子 第4个公共因子中的载荷正向主要集中于X30、X39、X40、X42、X46、X48、X49，而负都接近于0，而负值都接近于0，说明第4个公共因子主要由这8个变量解释，而这些变量主要是关于数学知识与上机指导相结合的科目，都可以与相关的软件结合起来，称为信息处理因子。

5)思想修养因子 第5个公共因子中的载荷正向主要集中于X1、X9、X16、X2、X25，说明第5个公共因子主要由这5个变量解释，这5个变量都属于思想教育的范畴，称为思想修养因子。

表3 旋转后12个公共因子解释的方差

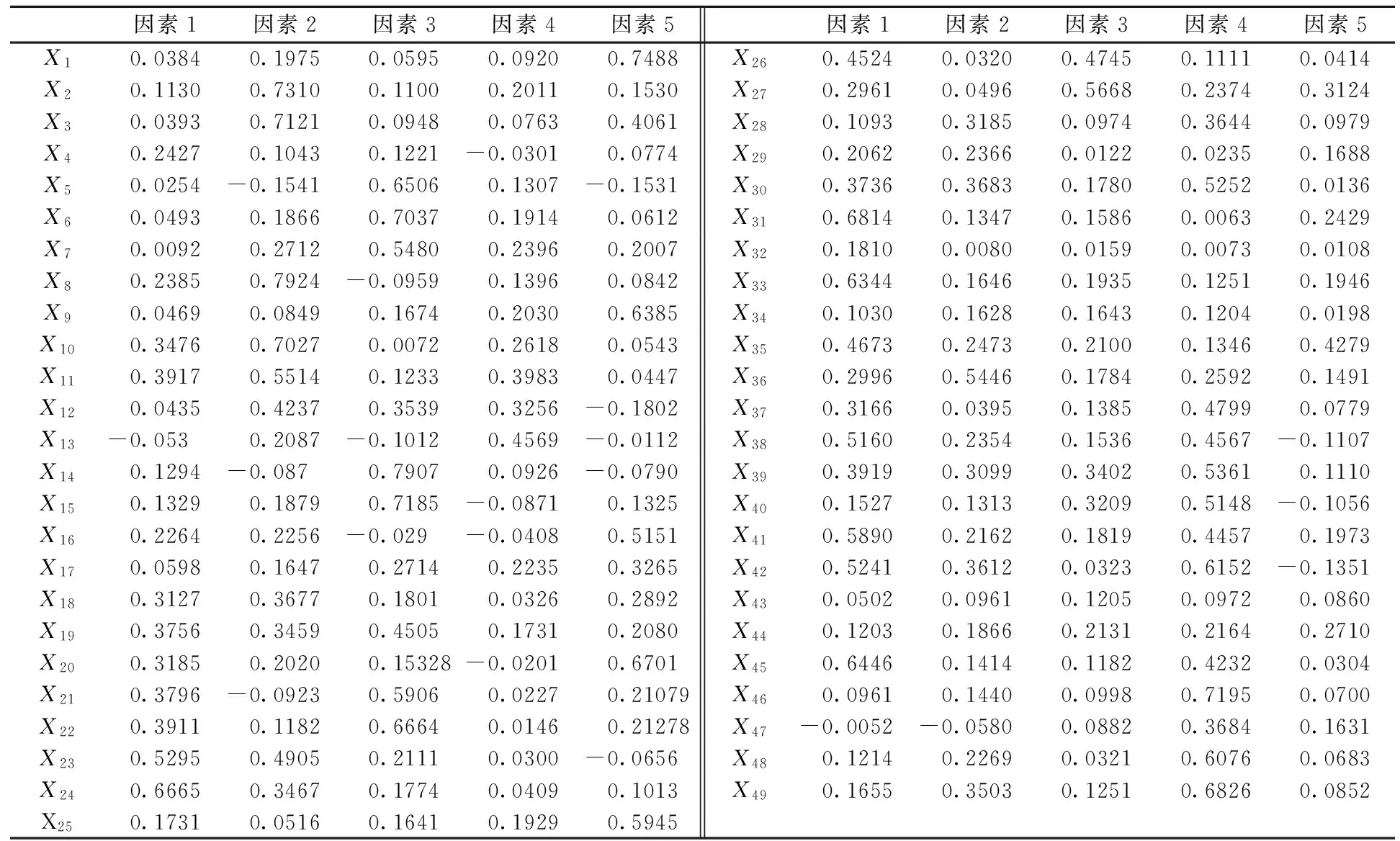
表4 旋转后前5个公共因子的因子载荷矩阵

2.5 因子得分

根据旋转后12个公共因子所解释的方差以及前5个公共因子的解释，对比信息与计算科学专业的专业要求可知，前5个公共因子基本上反映了该专业所需要的能力，因而可以计算前5个公共因子的因子得分对学生在各种能力上的排名，以此可以分析每名学生的能力大小。

为了根据前5个公共因子对学生的综合能力进行分析与评价，以表3中前5个公共因子(记为Factor1,Factor2,Factor3,Factor4,Factor5)对应的方差贡献率为权数根据下式计算综合因子得分:

Y=0.23Factor1+0.22Factor2+0.22Factor3+0.21Factor4+0.12Factor5

表5列出了根据前5个公共因子得到的信息与计算科学专业的学生在综合排名排列前10名和后10名的学生学号与综合得分。根据计算结果，前5名都在0816122班，并且在前10名的学生中，有9个是0816122班的；而在倒数10名的名单中，则有8个是0816122班的。由这不难发现，0816122班学生的学习成绩两极分化严重，形成了鲜明的对比，相比之下，0816121班的学生内部差距较小。

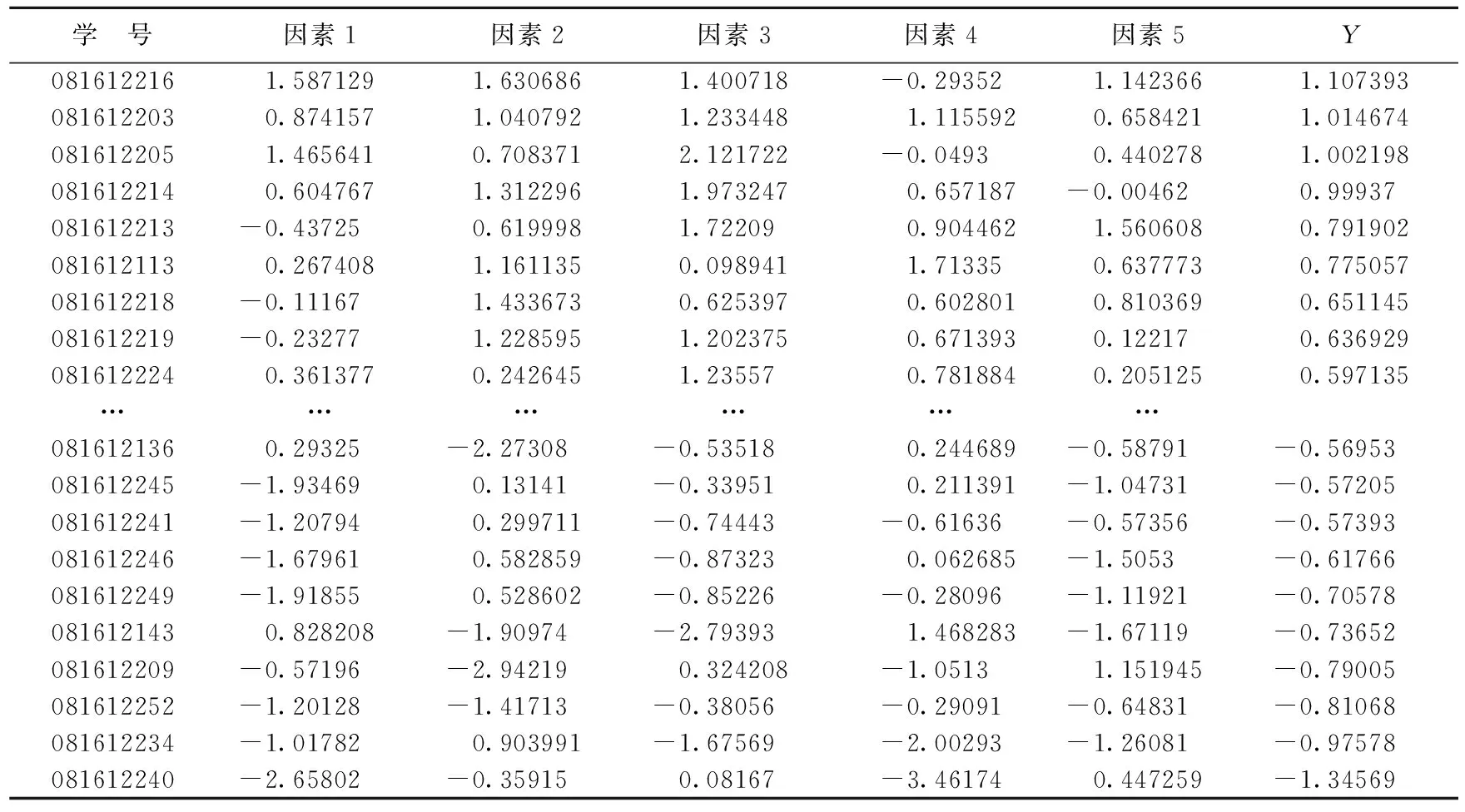
表5 综合排名前、后各10名

从学生个体来说，还可以从表5中看到每位学生在信息处理、计算能力、表达能力、抽象思维和品德修养5方面的优劣势。以第1名同学为例，抽象思维、计算能力、表达能力和品德修养方面的学科都是其强项，其中最具优势的是抽象思维的科目，因为其在众因子得分中是最高的，但信息处理能力较差，对于需要计算机与相关应用软件解决问题的课程如建模实践、信息与编码课程设计、数据分析与SAS应用实验、数据库原理与应用等科目，其Factor4是负数，表明是有所欠缺的内容。第2名同学5个因子得分都是正数，表明其各科的发展较为均衡全面，而且抽象思维、信息处理、表达能力最强。第3名同学5个方面的优劣情况与第1名同学相似，其最大的优势是表达方面的科目，对应的因子得分2.12非常高，说明外语类的科目是其强项。类似的可以分析其他每位学生各种能力的强弱和各门功课优劣等。

3 结 语

对于信息与计算科学专业的学生，把影响学生综合得分的主要因素概括为5个方面：计算能力、抽象思维、表达能力、信息处理、品德修养。可以通过计算因子得分和相应的权重来计算综合得分，这样排名结果可以减少主观因素和外界的干扰事项，更符合实际情况，使得所得的结果更具说服力。对学生而言，通过自己在这5方面的因子得分，知道自己的长处，看到自己的不足，扬长避短，并且可在以后的学习中有意识地在有欠缺的方面多加注意和锻炼，使自己更全面综合地发展；对于老师来说，可以通过因子得分和综合排名客观地了解学生各方面的特点、优劣势和不同能力上的差异，也为老师有针对地指导学生提供了客观的依据，有助于实现因材施教，挖掘学生的发展潜力。与此同时，其也有利于教师分类分层教学，为学生能力的全面发展和综合素质的提高提供借鉴和帮助，使教育教学工作更具科学性、针对性、合理性。

[1]杨晓明. SPSS在教育统计中的应用[M]. 北京: 高等教育出版社, 2004: 41-329.

[2] 吴海英, 张杰. 学生成绩排名的综合评价模型[J] . 大学数学, 2006, 22(4): 142-145.

[3] 张琼. 因子分析在学生成绩综合评价中的应用[J] . 惠州学院学报(自然科学版), 2010, 30(3): 40-45.

[4] 张驰. 师专数学专业学生知识能力结构的因子分析[J] . 四川师范大学学报(自然科学版), 1998, 21(3):336-340.

[5] 王成,王继顺. 基于因子分析与聚类分析的学生成绩综合评价[J]. 甘肃联合大学学报(自然科学版),2011,25(1):26-30.

[编辑] 洪云飞

10.3969/j.issn.1673-1409(N).2012.10.002

O213

A

1673-1409(2012)10-N004-04