多点激励下高墩大跨桥梁抗震性能分析
2012-11-20李正英王泽国牟德健
李正英,王泽国,牟德健
(重庆大学 土木工程学院,重庆 400030)
桥梁工程在地区与地区之间的交流中起到了纽带的作用。在我国西部,由于山高谷深,地形高低起伏,使得西部地区修建的桥梁往往墩高较高、跨度较大[1-2]。而西部相当一部分地区为地震多发区,桥梁结构的破坏将导致救灾工作的困难及巨大的人员伤亡和经济损失,因此随着西部地区该类高墩大跨桥梁的不断出现,有必要详细研究其在地震作用下的抗震性能及破坏特征,从而为该类桥梁抗震及减震设计提供参考,以提高该类桥梁的抗震性能。本文基于OpenSEES平台,采用非线性动力时程分析方法研究在多点激励情况与一致激励情况下高墩大跨桥梁的地震反应特征及破坏过程,以期为高墩大跨连续刚构桥的抗震及减震设计提供依据。
1 多点激励下结构动力分析方法
对于大跨度的结构,由于其支座空间位置的变化引起地震地面运动的差异导致多点激励问题的产生。多自由度体系在地震多点激励下的运动方程可写成[3]式中,xs为结构非支承节点绝对位移,xg为支承节点位移。质量矩阵、阻尼矩阵和刚度矩
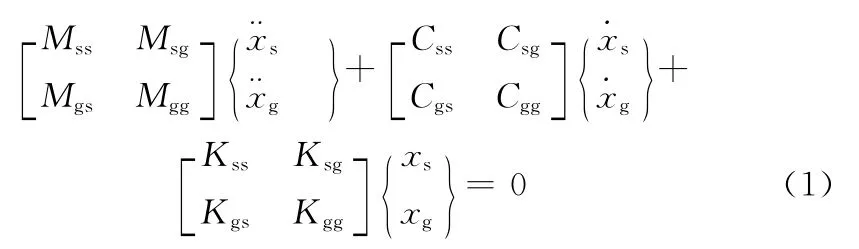
阵中的非对角项反映了结构非支承节点自由度与支承节点自由度间的相互影响。基于上述方程,求解结构地震反应,目前主要采用动力时程分析法,而多点激励问题的动力时程分析常用的方法有[3-5]:相对运动法,大质量法、位移输入法。相对运动法[3]的基本思想是将结构响应分解成拟静力项(结构由于强迫支座移动产生的静内力)和动力项(惯性力项)2部分,然后叠加得到总反应,由于相对位移法基于叠加原理,当涉及非线性地震反应时,不再适用。此时只能采用大质量法和位移输入法。大质量法[4]将结构基础假设为一个或多个附着于结构基础或支撑点的大质量单元,结构动力分析时,在大质量点施加动力模拟地面运动,在通用的有限元软件,如ANSYS、SAP中通常采用该方法。本文基于OpenSEES平台进行结构抗震性能分析,其多点激励地震反应分析的计算方法是基于位移输入法,位移输入法是在基底直接施加地震动位移[5],其原理如下。对于方程组(1),第一个方程可写为
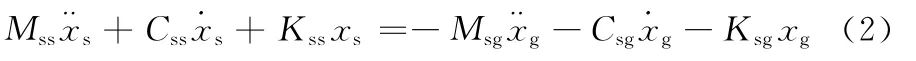
对于采用集中质量矩阵的模型,方程中的Msg为0,而阻尼项影响较小,可忽略不计,因此上式可写为:
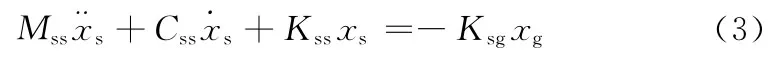
在结构支承点处输入地震激励位移时程,求解方程即可得到各节点的绝对位移反应。
2 桥梁模型
以西部开发省际公路通道重庆至长沙公路某段公路桥作为桥梁原型,主桥跨度为90+170+90m,上部结构采用预应力混凝土连续刚构箱梁,箱梁高度以及箱梁底板厚度按1.8次抛物线变化;其中箱梁跨中高度3.5m,根部高度10.5m,且箱梁跨中底板厚32cm,根部底板厚100cm。箱梁顶板厚度28cm,腹板厚度按直线变化,其中跨中厚40cm,根部厚70cm。主桥桥墩墩身采用双肢等截面矩形空心墩,墩高90m,肢间净距8m,主墩承台厚4m。基础采用桩径2.8m的钻孔灌注桩,每墩共8根桩,平面按梅花形布置。主桥箱梁及桥墩均采用C55的混凝土,钢筋采用HRB335热轧带肋钢筋和R235热轧光圆钢筋。桥址场地类别为Ⅱ类,整桥模型见图1。
基于OpenSEES平台建立分析模型。一般而言,桥梁的上部结构在地震中应力达到塑性范围的可能性比较小,地震破坏主要集中在桥墩和支座,因此对于桥面主梁采用弹性梁单元进行模拟,每2m划分1个单元,沿桥纵向的主梁为曲线变截面,建立模型时作了一定简化,假定其截面从墩顶截面至跨中截面之间按直线变化。桥墩是桥梁结构抗震设计的主要部位,在能力设计中,一般将下部结构设计形成塑性铰以消耗地震能量[6]。而OpenSEES中的弹塑性纤维单元在计算中可以考虑强度、刚度退化的影响[7],因此桥墩模型采用基于纤维模型的弹塑性空间梁单元模拟,在桥墩中部单元长度为2m,接近桥墩顶部及底部,单元长度为1m。桥墩单元横截面上混凝土纤维的划分,按照沿长度方向划分为10个纤维,沿宽度方向划分为5个纤维。混凝土纤维单元的应力应变关系采用Kent-Scott-Park模型[8],钢筋纤维的应力 应变关系采用 Giuffré-Menegotto-Pinto[9]模型。墩底与基础为刚接。
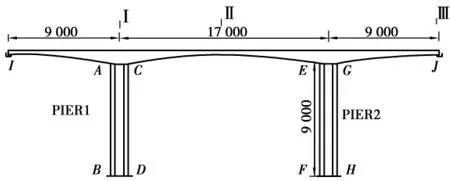
图1 纵桥向桥梁模型(单位:cm)
3 地震动输入
地震波作为地震释放出来的能量由震源经不同的地形及介质条件、不同的路径传至地面,因而其反映到地面不同位置处的地震动必然存在着某种程度上的差异,多点激励输入是考虑这些因素引起的差异,在结构各支点输入不同的地震动。目前主要采用的多点激励输入方法主要有行波输入和多点输入。考虑行波效应的行波输入时,各点输入地震动满足[10]

式中:v是视波速;C是振幅衰减系数,其值小于等于1,表征地震动沿距离的耗损,一般沿结构长度方向振幅衰减不明显时,取C=1;dAB是A、B两点间的距离。该桥桥址场地类别为Ⅱ类,因此选用与桥址场地类别相近的Ⅱ类场地的两条实际地震动和一条人造地震波作为地震动输入,表1为实际地震动基本信息。

表1 实际地震动基本信息
4 结果分析
4.1 行波效应分析
采用行波输入,输入地震动为上述3条地震波,并调整加速度峰值为156.8cm/s2。地震波沿纵桥向从左到右输入,各墩间距分别为83、170、83m,分别采用视波速无穷大的一致激励和视波速为200,500,800、1000m/s行波输入进行地震响应分析。
图2和图3给出了3条地震波作用下各墩墩顶和墩底截面内力峰值平均值随视波速的变化曲线。从图中看出,随着视波速的增大,视波速与内力之间的规律性:一致激励情况下的桥墩弯矩均大于行波效应下的反应;而行波效应下的墩底剪力并不都小于一致激励情况,如墩底B、H点和墩顶E点的剪力最大值发生在视波速为500m/s时,这几个截面剪力最大值分别为一致激励的1.01、1.02和1.09倍,墩底D、F点剪力最大值发生在视波速为200m/s,其值为一致激励反应的1.08、1.08和1.03倍。可见,考虑行波效应时截面弯矩和墩顶剪力均小于一致激励情况;而在某些视波速下墩底剪力大于一致激励情况,但相差不大。因此可以看出,与一致激励相比,行波效应对此类高墩大跨连续刚构桥桥墩的地震反应是相对有利的。
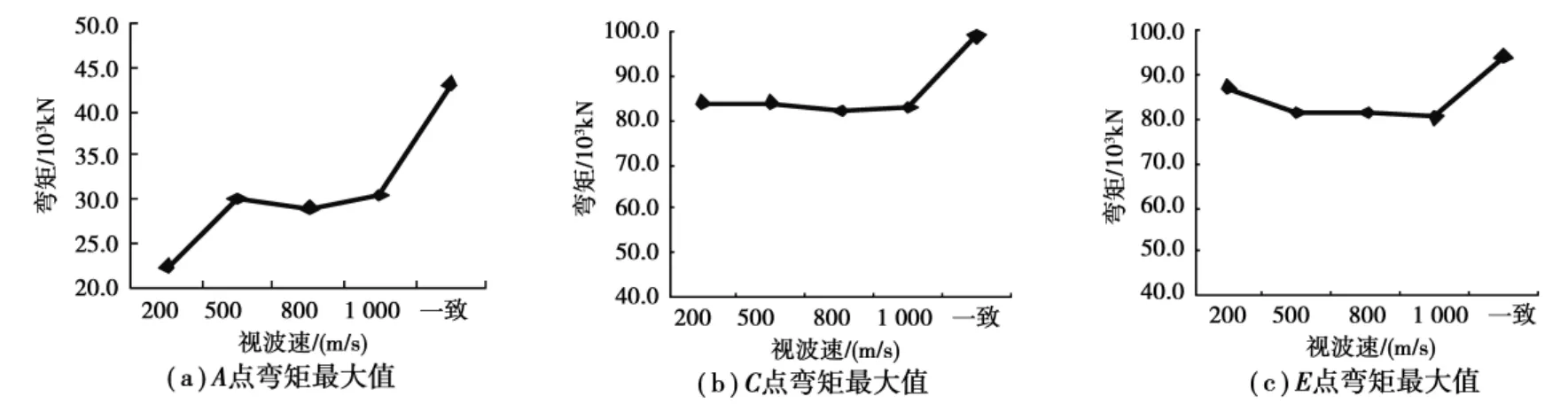
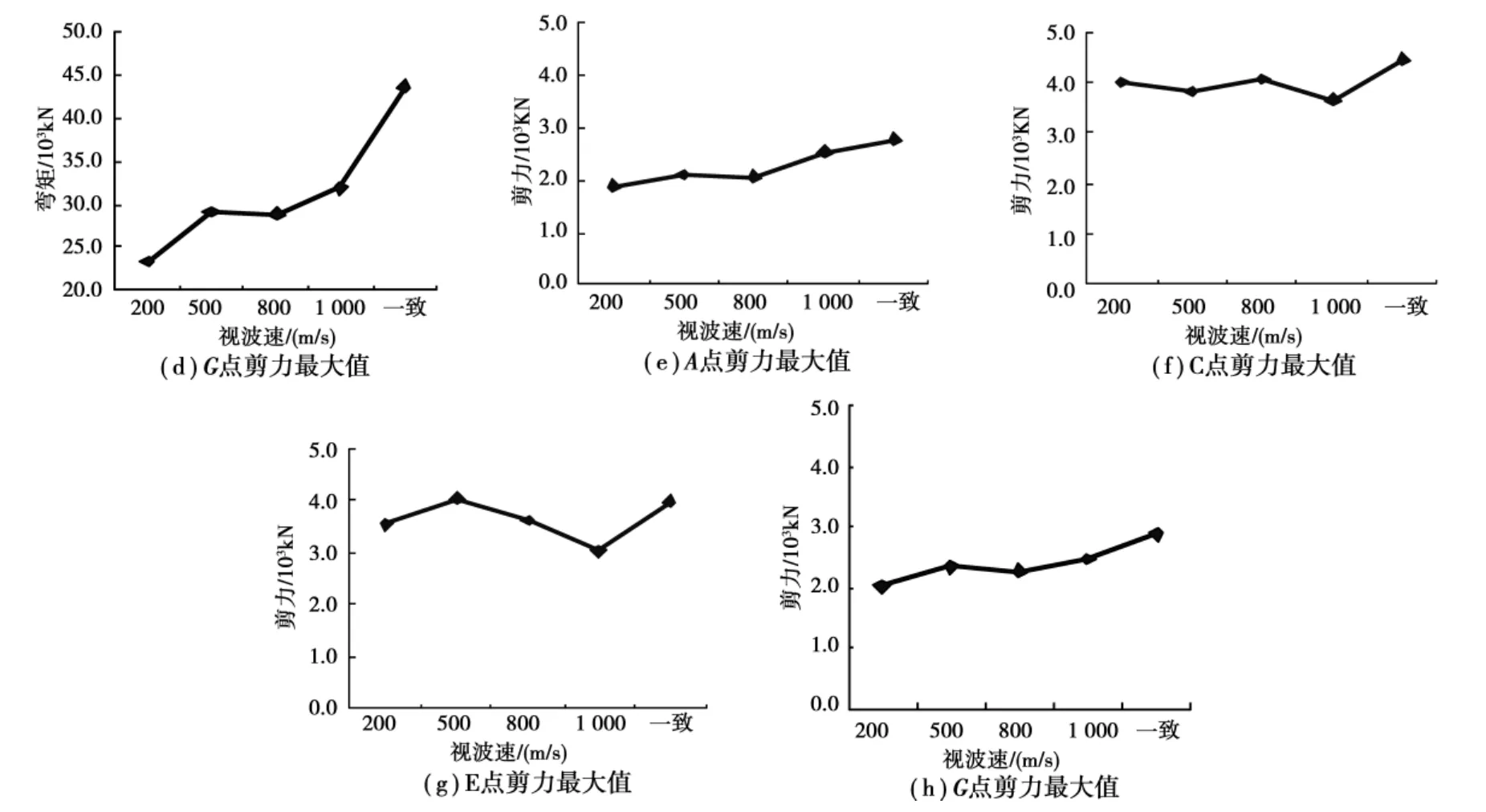
图2 墩顶内力峰值行波效应曲线
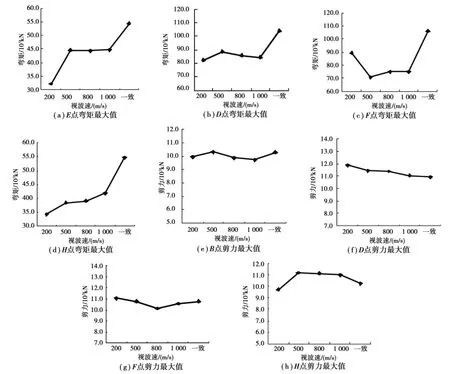
图3 墩底内力峰值行波效应曲线
4.2 多点激励下破坏过程分析
为了得到不同强度下结构的抗震能力,采用动力增量分析方法。动力增量分析方法通过一系列的加速度调整系数(factor),将一条地震动扩展为一组地震动,并通过这组地震动分别对分析对象进行非线性时程分析,在分析过程中,记录结构从弹性反应到出铰直至破坏过程中关键截面的地震反应变化规律。选用上述3条地震波,对结构纵向采用行波输入的多点激励方式,进行结构地震反应的增量动力分析。行波输入时,视波速为500m/s。表2给出了在3条地震动多点激励输入下结构各关键截面首次出铰和达到破坏时的顺序以及对应的地震动加速度峰值大小。
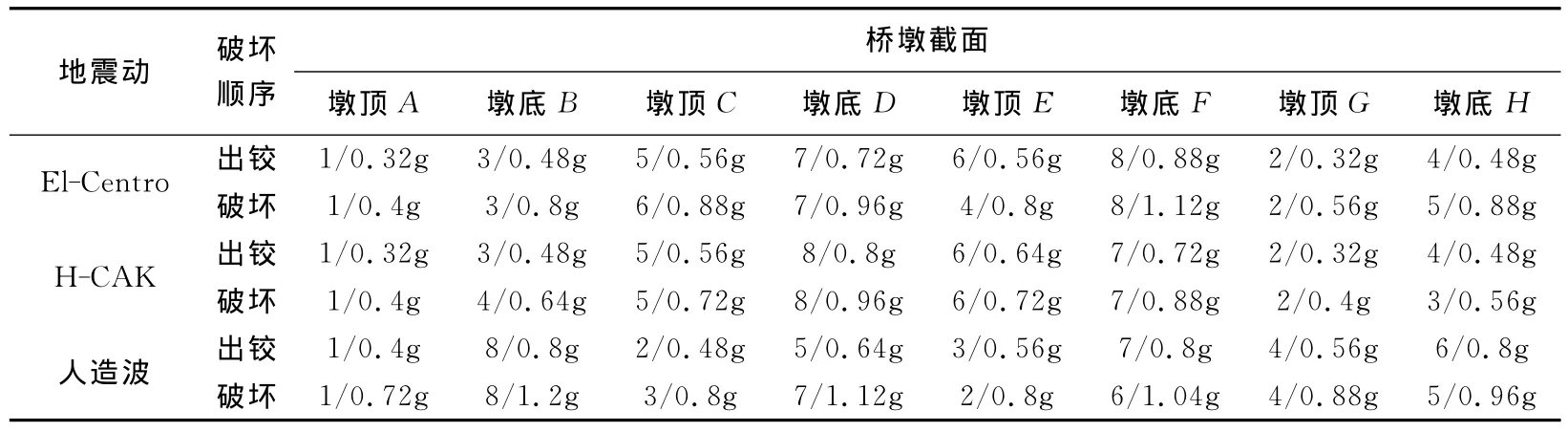
表2 行波输入下桥墩出铰和破坏顺序及相应的加速度峰值
从表中数据可以看出:1)对于出铰的顺序及位置来说,3条地震波每个单墩均为墩顶先于墩底出铰。El-Centro波和H-CAK波桥梁墩顶、墩底的前6个出铰顺序相同,均在桥梁两侧AB墩和GH 墩先出铰,然后内侧两墩CD墩和EF墩才出铰。人造波与两实际地震波的出铰顺序差别较大,为桥梁墩顶截面全部出铰后,墩底截面才开始出铰。2)各桥墩的破坏顺序与出铰顺序基本一致,El-Centro波和H-CAK波作用下是桥梁两侧的AB墩和GH 墩墩顶先破坏,随后各自的墩底达到极限状态;而内侧两墩CD墩和EF墩是在两外侧墩AB墩和GH墩达到极限状态后才破坏。人造波作用下各墩墩顶截面均达到极限状态后,墩底截面才破坏。
5 结 论
基于OpenSEES平台,建立高墩大跨桥梁的弹塑性结构模型,分析在多点激励行波效用作用下桥梁结构的地震反应特性及不同强度地震动下高墩桥梁的抗震性能。通过桥墩出铰顺序及位置、墩顶及墩底内力和墩顶位移反应比较得出以下结论。
1)行波效应对高墩连续刚构桥桥墩地震反应的影响是相对有利的。考虑行波效应时,桥墩截面弯矩和墩顶剪力均小于一致激励情况;而在某些视波速下墩底剪力大于一致激励情况,但相差不大。
2)高柔的桥墩在水平地震作用下往往以弯曲型破坏为主,由于高墩桥梁墩身自重对轴力的贡献较大,在一定的轴压比范围内,轴力较大有利于截面抗弯能力的提高,因此墩底截面的抗弯能力要大于墩顶截面。在行波输入下,单墩首次出铰或发生破坏往往发生在墩顶截面;两外侧薄壁墩AB墩和GH 墩较之内侧薄壁墩CD墩和EF墩往往先出铰或达到破坏状态,因此对于此类双肢薄壁空心墩高墩桥梁,在设计中除了墩底截面加强配筋外,还应加强墩顶截面和两侧薄壁墩的截面配筋设计。
3)地震动的频谱特性对结构的破坏顺序有较大影响,不同地震波作用下结构的破坏顺序是不尽相同的。
本文在研究桥梁多点激励反应时,只考虑了空间地震动的时滞效应,而部分相关效应以及局部场地效应等因素的影响,将进一步深入研究。
[1]刘健新,赵国辉.“5·12”汶川地震典型桥梁震害分析[J].建筑科学与工程学报,2009,26(22):92-97.
[2]梁智垚,彭伟.桥梁结构弹塑性地震反应分析新进展[J].世界地震工程,2007,23(4):163-168.
[3]范立础.桥梁抗震[M].上海:同济大学出版社,1997.
[4]周国良,鲍叶欣,李小军,等.结构动力分析中多点激励问题的研究综述[J].世界地震工程,2009,25(4):25-31.
[5]柳国环,李宏男,林海.结构地震响应计算模型的比较与分析[J].工程力学,2009,26(2):10-15.
[6]Rosario C,et al.Problems in applying code-specified capacity design procedures to seismic design of tall piers[J].Engineering Structures,2009,31:1811-1821.
[7]Mazzoni S,McKenna F,Michael H.Open system for earthquake engineering simulation user manual[R].Pacific Earthquake Engineering Research Center, University of California,Berkeley,2005.
[8]Scott A ,Park R ,Priestley M J M.Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates[J].ACI Structural Journal,1982,79(1):13-21.
[9]Menegotto M,Pinto P E.Method of analysis for cyclieally loaded reinforced concrete plane frames including changes in geometry and non-elastic behavior of elements under combined normal force and bending[C].Proceedings,IABSE Symposium on Resistance and Ultimate Deformability of structures,Lisbon,1973,15-22.
[10]潘强,方诗圣,程晓东.高墩大跨连续刚构桥地震反应的行波效应研究[J].湖南工程学院学报,2010,20(2):82-85.
