一杯陈年佳酿 令人回味悠长
——对一个三角最值问题的深入探究
2012-11-20柯桥中学浙江绍兴312030
● (柯桥中学 浙江绍兴 312030)
一杯陈年佳酿令人回味悠长——对一个三角最值问题的深入探究
●樊宏标(柯桥中学 浙江绍兴 312030)
人教版《数学》选修4-5作业本第71页的第17题如下:

此题有一定的难度,学生不易求解.从作业的反馈情况来看,大致有2类典型的错误.
错解1由基本不等式,得
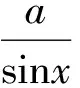



错解2由柯西不等式,得


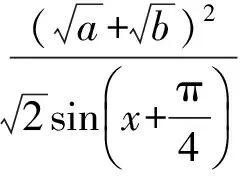

1 错因剖析

错解2运用柯西不等式进行求解,同样忽视了等号成立的条件.若等号成立,则必有
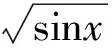

由此可知,忽视等号成立的条件是学生利用不等式求最值最容易犯的错误.因此,在利用不等式求最值时,教师要提醒学生注意“等号成立的条件”,养成“即时验证”的良好习惯.
2 解法探究
解法1利用柯西不等式
由柯西不等式,得

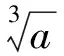

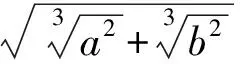
再由柯西不等式,得

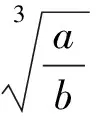
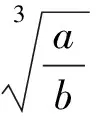

由于sin2x+cos2x=1,因此,对原题加以拓展,可转化为:
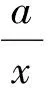
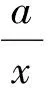
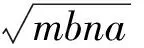


m2+n2=(x2+y2)(m2+n2)≥(mx+ny)2,

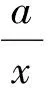

当且仅当

故
解法2待定系数法
设m,n为正的常数.由柯西不等式,得
(1)
(m2+n2)(sin2x+cos2x)≥(msinx+ncosx)2.
(2)
由式(1)和式(2),得
而式(3)中等号成立的条件是式(1)和式(2)中的等号同时成立,即
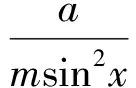
亦即
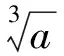
代入式(3),整理得
在日常的教学中,教师往往会到此为止,认为思路已经打通,源头已经找到,方法已经点明,解题过程也就自然完成了.但笔者认为数学解题的基本程式包括简单模仿、变式练习、自发领悟、自觉分析[1],因此,笔者引导学生继续分析题目的结构特征,看还有没有其他更好的解法.不料这一问,激起了学生极大的兴趣,很快就有学生提出新的想法,共同探究,得到如下2种解法.
解法3运用基本不等式
考虑到
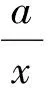

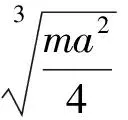

当且仅当
即

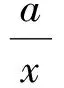
解法4利用导数
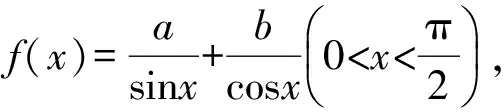

令f′(x)=0,即

因为

所以
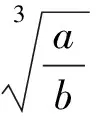
又因为
sin2x+cos2x=1,
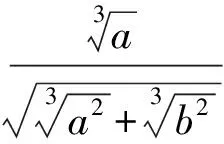
此时
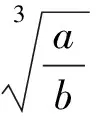
f(x)的单调性分析如表1所示.
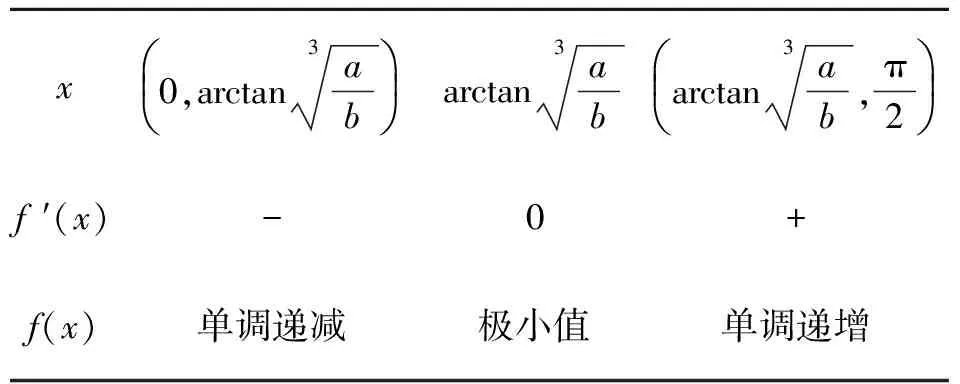
表1 f(x)的单调区间
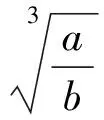
3 拓展延伸
课后,笔者又进行了深入研究,对于上述问题,利用赫尔德(Hölder)不等式可作进一步拓展,结论如下:

(1)当t∈(0,2)时,y取得最大值;
(2)当t∈(-∞,0)∪(2,+∞)时,y取得最小值.

asintx+bcostx,
从而
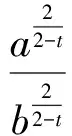

sin2x+cos2x=1,
从而
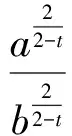
同理可证,当t∈(-∞,0)时,
点评本文一开始的作业习题显然是上述定理取t=-1的特殊情况,该题若用Hölder不等式证明,则更简单.



4 几点思考
(1)在新课程理念下,笔者认为教师的解题教学不是“讲习题”,而是“用习题”.教师的作用就在于挖掘习题的内涵,使之更为丰满、生动,更具联系性.
(2)教学中应把“探索作为数学教学的生命线”(布鲁纳).通过创设恰当的问题情境,促进学生在活动中感悟并获得数学知识与思想方法.在知识的发生、发展与运用的过程中,培养学生的思维能力、创新意识和应用意识.
(3)促进课堂互动,创建宽松、和谐的学习环境.教学中,要充分发挥教师的主导作用,以问题为中心,以探索为生命线,注重优化学生的思维品质.数学解题教学绝对不能就题论题,就答案而讲答案,而更应关注为什么这样解,以充分暴露解题的思维过程,并不断地引导学生对典型例题作解题后的反思.让他们通过已知学未知,通过分析已经解决的习题去领悟解题思想,通过解题思想去驾驭并活化知识与方法,增强分析能力,提高领悟水平,优化思维品质,从而真正提高学生分析问题和解决问题的能力.
(4)注重问题的引申与拓展.从一道题出发,进行多角度、多方位的思考,并纵横联想、拓展延伸.这样处理一道题,便可以收到多方面的教学效益,既巩固了大量的基础知识,又拓宽了学生的思维空间.真是“典型习题剖析透,一石三鸟硕果收;纵横驰骋留不住,海天宽阔任遨游”!
[1] 樊宏标.从一个案例谈数学解题的基本程式[J].高中数学教与学,2010(7):5.
