基于神经网络的注塑机料筒温度解耦控制策略研究＊

李明辉 李正琦

（1浙江温州轻工研究院 浙江 温州 325000）（2陕西科技大学后勤集团 西安 710021）

基于神经网络的注塑机料筒温度解耦控制策略研究＊

李明辉1李正琦2

（1浙江温州轻工研究院 浙江 温州 325000）（2陕西科技大学后勤集团 西安 710021）

针对注塑机料筒温度的耦合性、非线性、时变性等特点，提出了基于神经网络的静态解耦和神经元自适应PSD相结合的控制算法，在实现料筒温度解耦的基础上对温度进行自适应控制。对该控制算法进行了仿真研究，结果表明，该控制算法能够较好地实现料筒温度控制，对提高料筒温度控制的快速性、准确性具有一定的参考价值。

料筒温度 静态解耦 PSD 自适应控制

前言

注塑机是把塑料原料加热溶化后注塑到模具中，经冷却形成塑料制品的一类机器。在塑料的注塑过程中，熔体的温度是一个很重要的参数。熔体温度决定于料筒温度和料筒内螺杆与塑料之间的剪切热，料筒温度过低和过高都会影响产品的最终质量。料筒温度过高时，筒内的塑料会发生降解；料筒温度过低时，塑料塑化不良，流动性差，制品成形性能不好。因此在注塑过程中，料筒温度控制成为影响注塑制品质量的关键技术。

1 料筒温度特性研究

料筒温度是指料筒表面的加热温度，是塑化装置的惟一外部供热。根据聚合物在料筒中的塑化机理，可分为三段加热：第一段是固体输送段，温度要低一点，但在加料口要进行冷却以防止温度过高而引起“架桥”现象，使加料不顺畅；第二段是压缩段，温度要高于第一段20～25℃；第三段是计量段，一般温度高于第二段20～25℃，以保证物料在熔融态料筒的表面温度和料筒内壁温度存在温度梯度，而料筒内壁温度才接近熔体的温度。有时在预塑时，储料室中熔体因吸收一部分剪切热而使实际温度高于料筒的温度。在储料室中熔体的温度与料筒温度、螺杆行程、螺杆转速和背压有关，但是在螺杆转速和背压一定的条件下，熔体温度与料筒温度大致成比例变化，而熔体温度直接影响熔体的粘度和流动性，所以，稳定料筒温度对控制储料室中的熔体温度有重要作用。

注塑机料筒温度各加热段的数学模型可用（1）式近似表示：

式中：k——比例系数；

T——惯性时间常数；

τ——滞后时间。

由于注塑机料筒没有设置冷却散热系统，因此塑料降温过程是完全依赖于自然散热的。由于料筒的壁较厚，自然散热的速度很慢，因此塑料升温和降温过程是一个典型的非线性大惯性过程。因为各个区间加热器的加热功率不同，同时各区间段内塑料总量也不相同，因此在加热过程中，各个区间段的温度不是同步变化的，存在着温度差异，因此相邻塑料加热区间段内塑料会进行热传递，导致加热区间段之间的温度会相互影响，具有耦合性。随着温度的升高，塑料的比热容、热扩散系数、导热系数、密度等参数也会发生变化，因此，注塑机的料筒温度具有多变量、非线性、强耦合、时变性等特点，所以上述3个参数并不是常数，而是随着时间的推移在发生变化。

目前，注塑机料筒温度控制有传统的开关控制、PID控制以及解耦控制等，但这类控制算法必须依赖于精确的数学模型，而注塑机料筒由于具有多变量、非线性、强耦合、时变性等特点，要想获得精确的数学模型很困难。在此，笔者采用基于神经网络的静态解耦和神经元自适应PSD（比例、求和、微分）相结合的控制算法，在实现料筒温度解耦的基础上对温度进行自适应控制，这样能够较好地提高系统的动静态性能。

2 基于神经网络的静态解耦

传统解耦理论将解耦分为静态解耦和动态解耦。因为按动态解耦原理设计补偿环节，在物理上不可实现或实现起来过于复杂，故在此采用静态解耦法。

由于神经网络可以以任意精度逼近任意解析非线性函数，而且具有学习、自适应能力，使它能够处理系统的非线性特性，同时又有很强的容错能力。因此神经网络成为了实现非线性系统控制的有力工具［1］。神经网络解耦原理就是设计一个计算机网络，用它去抵消过程中的关联。使包含解耦控制器在内的广义对象传递函数变为对角阵，由此解除过程中的耦合，使控制系统变为单回路系统。由于注塑机料筒温度具有非线性、时变性等特点，采用传统解耦方法实现复杂或难以实现，又无法在整个工作曲线范围内完成解耦控制。而人工神经网络借助于可训练性和结构的通用性，赋予其自适应能力，能逼近任意L2上的非线性函数，且不需要精确的对象模型，实现起来简单方便，能够满足解耦控制要求，从而构成基于神经网络的解耦控制。神经网络解耦控制系统方框图如图1所示［2］。

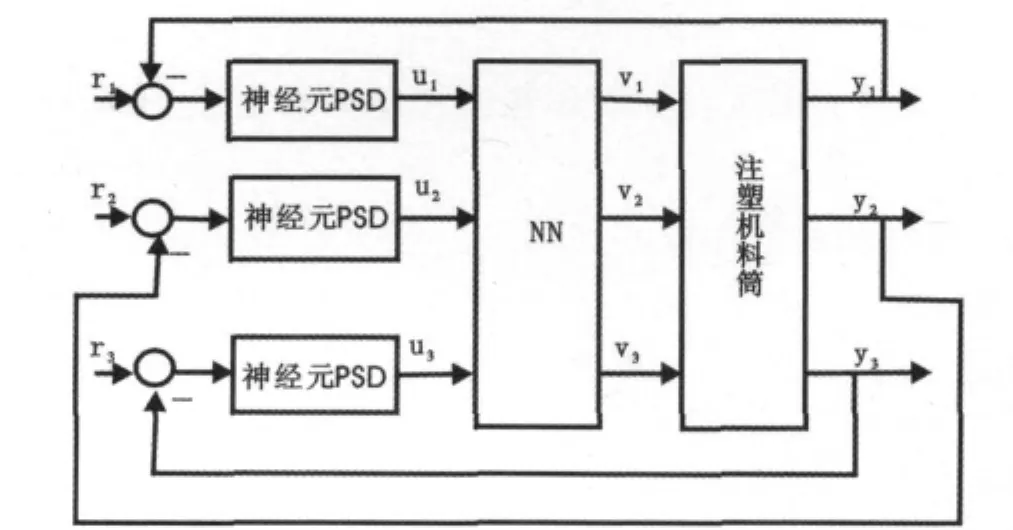
图1 神经网络解耦控制方框图Fig.1 Control diagram of neural network decoupling

图1 中r1、r2、r3分别表示注塑机料筒三段温度设定值；u1、u2、u3分别为三个神经元PSD控制器输出的控制信号；v1、v2、v3分别为经过解耦后作用在注塑机料筒上的加热丝的控制电压；y1、y2、y3分别为注塑机料筒三个加热段输出的实际温度。

解耦的目的是要解除注塑机料筒三个加热段之间的耦合关系，即y1只跟随u1，y2只跟随u2，y3只跟随u3的变化而变化。这里采用包括神经网络在内的广义对象的Bristol第一系数矩阵，若用Y表示被控量，U表示控制矢量，则有：

式中：Y＝［y1y2y3］T，U＝［u1u2u3］T

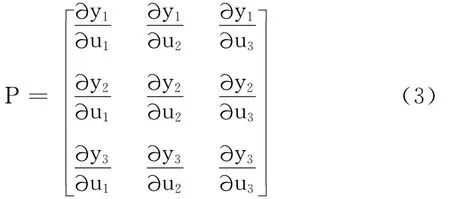
如果广义对象是解耦的，则矩阵P应为对角阵，因而图1的神经网络解耦控制系统的解耦训练目标定义如下：

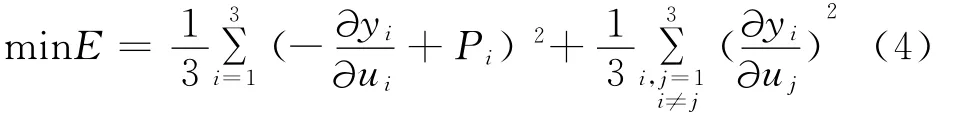
式中：Pi——解耦系统广义对象第i（i＝1，2，3）通道的增益。

神经网络解耦补偿环节采用具有一个隐含层的BP网络，输入节点3个，分别为控制量u1，u2，u3；输出节点3个，分别为注塑机三段加热电压，隐层节点数7个。其结构如图2所示。

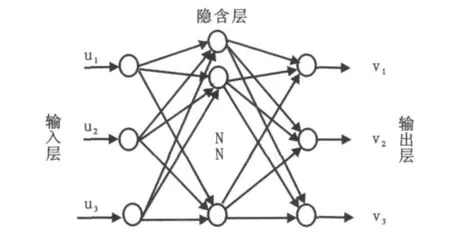
图2 BP网络结构图Fig.2 Chart of BP network

神经元的活化函数取为：

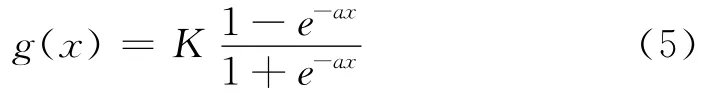
神经网络解耦补偿环节采用剃度算法来修正网络加权系数，即：

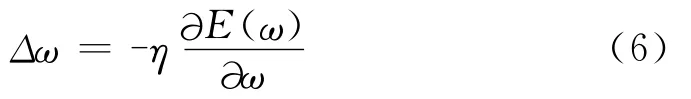
式中：η——学习速率。

可以证明，当采用至少含有一个隐含层的前馈网络时，只要隐含层的个数足够多，且隐含层神经元活化函数为非线性可微函数，而η又足够少，则剃度算法一定收敛［3］。

将（4）式展开并对ω求导后，即可根据（6）式求得加权系数的修正值Δω。

3 神经元自适应PSD控制

3.1 PSD控制

PSD控制规律是1983年Marsik和Strejc根据控制过程误差的几何特性建立的性能指标，提出无需辨识的自适应控制。

类似于增量式PID控制规律，PSD控制规律为［4］：

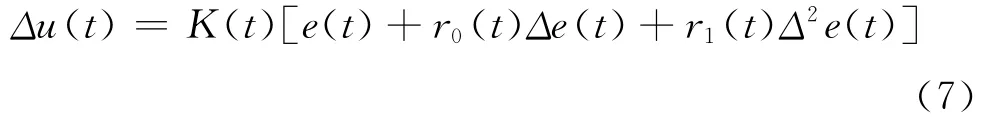
式中：u（t）——控制输入；

r0（t）、r1（t）——分别为比例、微分系数；

e（t）、Δe（t）、Δ2e（t）——分别是控制过程误差、误差的一次和二次差分。

它们构成了控制器的输入信号，且分别为：

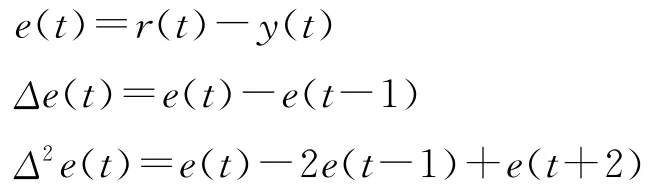
其中r（t）和y（t）分别为期望输出和对象的实际输出。

3.2 神经元自适应PSD控制算法

由单神经元构成的自适应PSD控制系统如图3所示。神经元PSD控制器的输出可表示为：

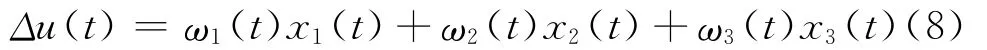
其中xi（t）（i＝1，2，3）为神经元输入信号，它们分别为：x1（t）＝e（t），x2（t）＝Δe（t），x3（t）＝Δ2e（t）。ωi（t）（i＝1，2，3）为对应于xi（t）输入的加权系数。

图3 神经元PSD控制系统Fig.3 Neurons PSD control system

在神经元学习过程中加权系数ω1（t）正比于递进信号ri（t），同时缓慢衰减，其学习规则如下：

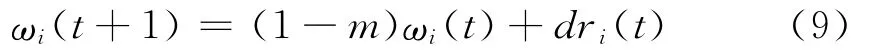
其中m，d＞0，d是学习速率，而ri（t）是递进信号并取作：

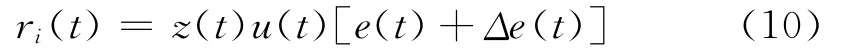
其中z（t）这里取作e（t）。

应用随机逼近理论，可以证明当m很小时，ωi（t）收敛到某一稳定值ω＊，使ω＊与期望值的偏差达到允许的范围。实际应用中可取m为0。

为保证学习算法的收敛性和控制的鲁棒性，采用规范化学习算法以构成单神经元PSD控制规律：

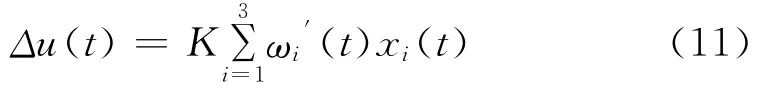
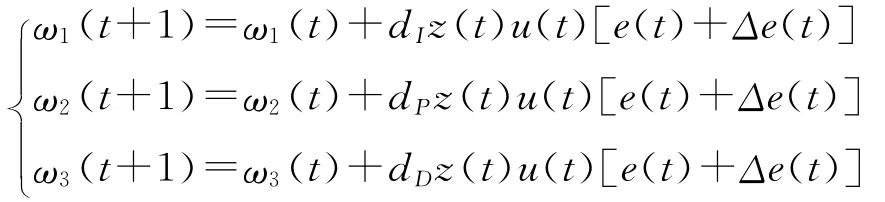
若sgn［e（t）］＝sgn［e（t－1）］，则K（t）＝K（t－1）＋CK（t－1）／Tν（t－1）。其中Tν（t）＝Tν（t－1）＋L＊sgn［｜Δe（t）｜－Tν（t－1）Δ2e（t）］；否则 K（t）＝0.75 K（t－1），即K（t）的增加速率反比于Tν（t），但当控制误差变号时，下降到上一时刻的75%。其中0.5≤L＊≤0.1，0.025≤C≤0.05。

4 仿真

4.1 网络训练

根据现场采集的被控对象输入输出数据对，利用Matlab强大的神经网络工具包，对上述的神经网络进行训练。简单方便地得出各个网络权值、阈值，得到所需的神经网络解耦、控制器。

4.1 仿真结果

笔者就本文所述的解耦控制算法用Matlab进行了仿真研究，仿真模型为［5］：

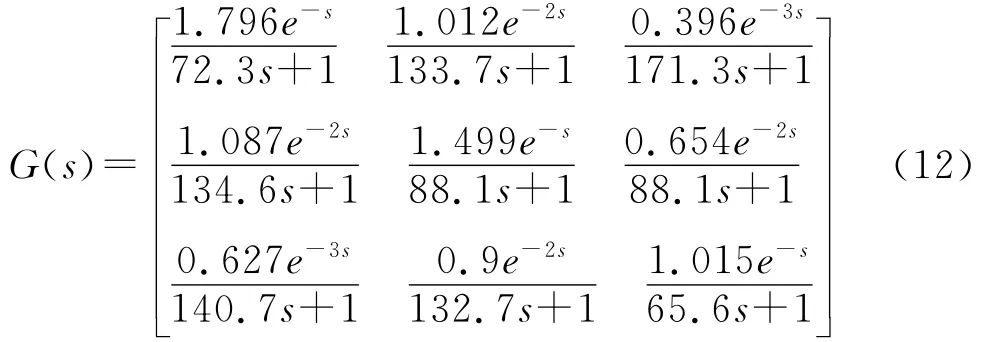
仿真结果如图4所示：

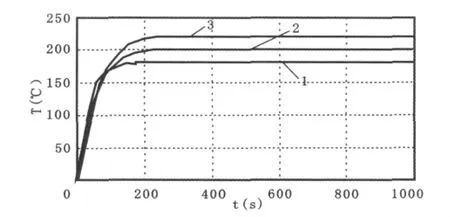
图4 注塑机料筒温度仿真曲线Fig.4 Temperature simulation curve of plastic injection machine

图4 中曲线1表示第1段料筒温度仿真曲线，设定值为180℃；曲线2表示第2段料筒温度仿真曲线，设定值为200℃；曲线3表示第3段料筒温度仿真曲线，设定值为220℃。

5 结论

笔者将以上所述的控制算法投入了运行，并对运行过程进行了监控，对注塑机料筒三段温度控制进行了测试，获得如图5所示的料筒三段温度响应曲线。图5中曲线1表示料筒第一段温度响应曲线，设定值为180℃；曲线2表示料筒第二段温度响应曲线，设定值为200℃；曲线3表示料筒第三段温度响应曲线，设定值为220℃。

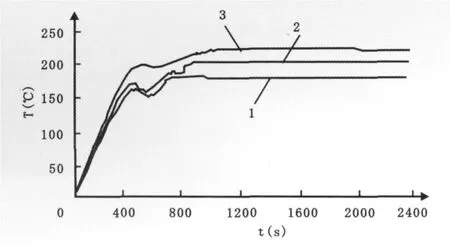
图5 注塑机料筒温度实际运行曲线Fig.5 Temperature actual operating curve of plastic injection machine

由图5可知，料筒温度响应均比较迅速，在15min左右达到设定值，稳态控制误差在±1℃以内。由此可见，笔者提出的控制算法对实现注塑机料筒温度的精确、快速控制具有重要的参考价值。

1 马平，杨金芳，崔长春，等.解耦控制的现状及发展.控制工程.2005，12（2）：97～100

2 舒迪前.预测控制系统及其应用.北京：机械工业出版社，1996

3 袁增任.人工神经元网络及其应用.北京：清华大学出版社，1999

4 李士勇.模糊控制神经控制和智能控制.哈尔滨：哈尔滨工业大学出版社，1998

5 孙锡红，苏兴.注塑机料筒温度的模糊神经网络控制研究.工程塑料应用.2009，37（10）：67～70

The Study of Temperature Control Strategy for Plastic Injection Machine Based on Neural Network

Li Minghui1，Li Zhengqi2（1Wenzhou Light Industry Research Institute，Zhejiang，Wenzhou，325000）（2College of Electrical and Information Engineering，Shaanxi University of Science ＆ Technology，Xi＇an，710021）

Aimed at the coupling，nonlinear and time－varying of injection molding machine barrel temperature，proposed a control strategy based on neural network static decoupling and neurons adaptive PSD.Which can realize temperature decoupling and adaptive control.The simulation results show that this control strategy can improve control performance greatly.

Barrel temperature；Static decoupling；PSD；Adaptive control＊

温州市科技项目（项目编号：H20100044）

TQ320

A

1002－2872（2012）04－0017－03

李明辉（1972－），博士，副教授；研究方向为智能控制。