知识蕴涵直觉主义逻辑系统

杜国平

（中国社会科学院哲学研究所，北京100732）

知识蕴涵直觉主义逻辑系统

杜国平

（中国社会科学院哲学研究所，北京100732）

在知识蕴涵命题逻辑的基础上，借助强知识蕴涵，可以构建知识蕴涵直觉主义逻辑系统。结合知识蕴涵逻辑和直觉主义逻辑的形式语义，可以证明知识蕴涵直觉主义逻辑系统具有可靠性和完全性。在该系统中，矛盾律仍然成立，但是排中律、双重否定消去律、司各脱法则都不再成立。在该系统中，弗协调逻辑和直觉主义逻辑的基本特征都被保留了下来，该系统给出了一个处理矛盾问题的既是弗协调的、又是直觉主义的兼容方案。

知识蕴涵；直觉主义；司各脱法则；矛盾

为了解决包含不协调信息的知识系统的推理问题，我们建立了知识蕴涵逻辑的命题逻辑系统、模态逻辑系统、时态逻辑系统以及谓词逻辑系统［1－9］，本文将在上述工作的基础上，在强知识蕴涵的基础上将知识蕴涵逻辑推广到直觉主义逻辑系统之中，建立知识蕴涵直觉主义命题逻辑系统。在该系统中，我们希望基本的直觉主义逻辑思想在其中得以体现，即排中律、双重否定消去律等在其中不是定理；当然，我们也希望在该系统中不矛盾律仍然是定理，但是司各脱法则不是定理，即弗协调逻辑的特征在该系统中仍然得以保持。

一、形式语言

定义1.1 知识蕴涵直觉主义命题逻辑的形式语言LIP和知识蕴涵命题逻辑语言基本相同，只是增加了一个初始符合∨。包括下列三类初始符号：

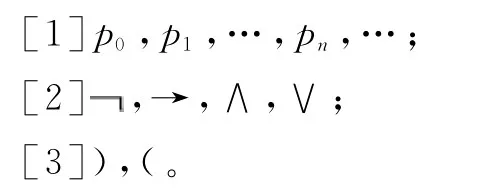
形式语言LIP中的第一类符号称为命题符号，第二类符号是命题联结词符号，第三类符号是左右括号。初始符号组成的有穷序列称为符，全体符所形成的集合记为Expr（LIP）。

定义1.2 LMP中的一个表达式是原子公式，当且仅当它是一个单独的命题符号。

由LIP中所有原子公式构成的集合记为Atom（LIP）。我们用大写字母A、B、C、D等表示任意的公式，用符号Σ、Γ、Δ等表示任意的公式集，由LIP中所有公式构成的集合记为Form（LIP）。

定义1.3 （Form（LIP））A∈Form（LIP），当且仅当它能（有穷次）由下列规则而得：

［1］Atom（LIP）⊆Form（LIP）；

［2］如果A∈Form（LIP），则（ A）∈Form（LIP）；

［3］如果A、B∈Form（LIP），那么（A∧B）∈Form（LIP）、（A∨B）∈Form（LIP）、（A→B）∈Form（LIP）。

括号省略规则与经典命题逻辑相同。

定理1.1（公式归纳原理） 令P是关于符的一个性质。如果：

［1］对于任何命题符p，P（p）；

［2］如果P（A）成立，则P（A）成立；

［3］如果P（A）、P（B）成立，则P（A∧B）、P（A∨B）、P（A→B）也都成立。

那么所有公式都具有性质P。

其他联结词通过定义给出：

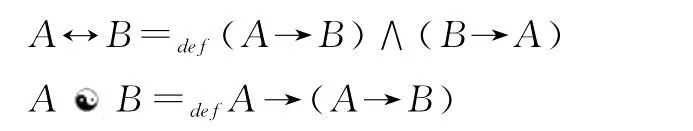
定义1.4 设A∈Form（LIP），Atomic（A）定义如下：

［1］如果A是原子公式，那么Atomic（A）＝｛A｝；

［2］如果A＝ B，那么Atomic（A）＝Atomic（B）；

［3］如果A＝B∧C，那么Atomic（A）＝Atomic（B）∪Atomic（C）；

［4］如果A＝B∨C，那么Atomic（A）＝Atomic（B）∪Atomic（C）；

［5］如果A＝B→C，那么Atomic（A）＝Atomic（B）∪Atomic（C）。

定义1.5 假设A、B是公式，称A、B相关，当且仅当

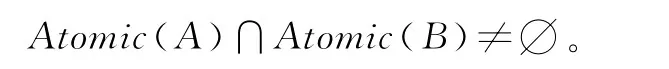
二、知识蕴涵直觉主义命题逻辑公理系统ID

定义2.1 知识蕴涵直觉主义命题逻辑公理系统ID的公理是下列形式的公式：

系统ID的推理规则只有一条，即分离规则（modus ponens）：由A和A→B可以推出B。简记为MP。

定义2.2 公式A由公式集Σ形式可推演，当且仅当存在公式序列：

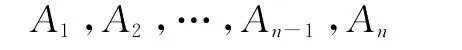
使得An＝A，并且每一个Ak（1≤k≤n）满足下列条件之一：

［1］Ak是公理；

［2］Ak∈Σ；

［3］有i，j＜k，使得Ai＝Aj→Ak。

如果公式A由公式集Σ形式可推演，则称Σ可推演出A，符号记为Σ├IDA，也简记为：Σ├A

定义2.3 如果公式A由Ø形式可推演，则称公式A是可证明的。由Ø到A形式可推演的一个公式序列称为公式A的一个证明。如果公式A是可证明的，则称公式A为系统ID的定理，符号记为├IDA，也简记为：├A。为了与其它的定理相区别，在下文中，我们将系统ID内的定理记为IDTh。

三、知识蕴涵直觉主义逻辑的形式语义

定义3.1 设LIP是一知识蕴涵直觉主义命题逻辑的形式语言，一个克里普克模型（简称模型）是一个三元组〈W，R，V〉，其中

［1］W是一个非空集，

［2］R⊆W×W，对于任意的w1，w2，w3∈W，w1Rw1，并且，若w1Rw2，w2Rw3，则w1Rw3；

［3］V：Atomic（LIP）×W→｛1，0｝，并且满足：对任一原子公式A，若w1Rw2，则V（A，w1）≤V（A，w2）。

［1］对任一原子公式A，V（A，w）∈｛1，0｝；

［3］V（A∧B，w）＝1，当且仅当V（A，w）＝1并且V（B，w）＝1；

［4］V（A∨B，w）＝1，当且仅当V（A，w）＝1或者V（B，w）＝1；

［5］如果对于任一w′∈W，若wRw′，当V（A，w′）＝V（B，w′），或者V（A，w′）＝0，V（B，w′）＝1，且A、B相关时，那么，V（A→B，w）＝1；

［6］如果存在w′∈W，wRw′，当V（A，w′）＝1，V（B，w′）＝0，或者V（A，w′）＝0，V（B，w′）＝1，且A、B不相关时，那么V（A→B，w）＝0。

［1］V（A，w）∈｛1，0｝；

［2］对于任意的w、w′∈W，如果wRw′并且V（A，w）＝1，那么V（A，w′）＝1。

定义3.3 设Σ⊆Form（LIP），A∈Form（LIP）。

Σ╞╱A表示Σ╞A不成立。

定理3.2 设A，B，C∈Form（LIP），

定理3.3 如果Σ╞A，并且Σ╞A→B，则Σ╞B。

四、ID的元理论

定理4.1 设Σ⊆Form（LIP），A∈Form（LIP）。

［1］如果├A，则╞A；

［2］如果Σ├A，则Σ╞A。

证明：

［1］施归纳于证明的结构。这只需证明形式系统ID中的公理都是有效的，并且其推理规则都是保持有效的。定理3.2和定理3.3已经证明了这两点。

［2］是［1］的推论。

定义4.1 设Σ⊆Form（LIP），Σ是ID协调的，当且仅当存在公式A，使得Σ├╱IDA。

为了方便，Σ是ID协调的也简称Σ是协调的。

根据Ax14，显然有：对于任一公式B，如果Σ是协调的，那么B和 B至少有一个不属于Σ。

定义4.2（强协调性） 设Σ⊆Form（LIP），Σ是强协调的，当且仅当Σ满足下列条件：

［1］Σ是协调的；

［2］对于任何A∈Form（LIP），Σ├IDA蕴涵A∈Σ；

［3］对于任何A、B∈Form（LIP），A∨B∈Σ蕴涵A∈Σ或B∈Σ。

定理4.2 设Σ⊆Form（LIP），A∈Form（LIP），并且Σ├╱IDA。于是Σ可以扩充为Σ′⊆Form（L′），使得Σ′是强协调集，并且Σ′├╱IDA。

证明：

因为形式语言LIP是一可数语言，所以令

（1）B0，B1，…，Bn，Bn＋1，…

是Form（LIP）中公式的任意一个排列。

定义一个Σn⊆Form（LIP）的无限序列如下：

令Σ0＝Σ。由Σn构造Σn＋1的规则如下：

［1］如果Σn，Bn├IDA，则令Σn＋1＝Σn；

［2］如果Σn，Bn├╱IDA，并且Bn不是析取式，则令Σn＋1＝Σn∪｛Bn｝；

［3］如果Σn，Bn├╱IDA，并且Bn是析取式B′n∨B″n，则有

或者Σn，Bn′├╱IDA

或者Σn，Bn″├╱IDA

令

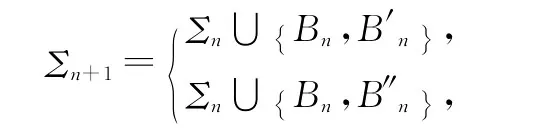
显然，有

（2）对于任意的n∈ω，Σn⊆Σn＋1

（3）对于任意的n∈ω，Σn├╱IDA

证明：

（4）Σ′├╱I DA

（5）Σ′具有强协调性。

首先证明（4）。假设Σ′├IDA。于是存在Σ′的有限子集｛A1，…，Ak｝使得A1，…，Ak├IDA。令，假设i＝max（i1，…，ik），则A1，…，Ak⊆Σi，因而有Σi├IDA，这与（3）矛盾。因此Σ′├╱IDA。

下面证明（5）。

因为存在公式A，Σ′├╱IDA，所以Σ′是协调的。这样Σ′满足了强协调性的第一个条件。

设B∈Form（LID）并且Σ′├IDB。则有：

（6）Σ′，B├╱I DA

因为如果Σ′，B├IDA，则有Σ′├IDB→（B→A），进而有Σ′├ICA，这与（4）矛盾。

设公式B在排列（1）中为Bm，则有

（7）Σm，Bm├╱IDA

因为如果Σm，Bm├IDA，则由于Σm⊆Σ′，故有Σ′，B├IDA，这与（6）矛盾。

根据由Σn构造Σn＋1的规则［2］～［4］可知Bm∈Σm＋1，因此有B∈Σ′，于是Σ′满足了强协调性的第二个条件。

设B′∨B″∈Σ′并且B′∨B″在排列（1）中为Bm。于是

（8）Σm，B′∨B″├╱IDA

因为如果Σm，B′∨B″├IDA，则Σ′，B′∨B″├IDA，则有Σ′├IDB′∨B″→（B′∨B″→A），进而有Σ′├IDA，这与（4）矛盾。

根据由Σn构造Σn＋1的规则［3］可知：或者B′∈Σm＋1或者B″∈Σm＋1，因此或者B′∈Σ′或者B″∈Σ′，于是Σ′满足了强协调性的第三个条件。

这样就证明了Σ′具有强协调性。

设Σ⊆Form（LIP）、A∈Form（LIP），并且Σ├╱IDA。令Σ0＝Σ。由定理4.2可知，Σ0可扩充为Σ1⊆Form（LIP），使得Σ1是强协调的并且Σ1├╱IDA。同样，Σ1可扩充为Σ2⊆Form（LIP），使得Σ2是强协调的并且Σ2├╱IDA，……。这样，对于任一n≥1，有Σn⊆Form（LIP），使得Σn是强协调的并且Σn├╱IDA，并且Σn⊆Σn＋1。

定义4.3 设Σ├╱IDA，与Σ、A相关的三元组m＊＝＜W＊，R＊，V＊＞是按照如下方式给出的。

W＊＝｛wn｜Σ⊆wn，wn是强协调的并且wn├╱IDA｝；

wiR＊wj当且仅当i≤j；

对于任一原子公式B，V＊（B，wn）＝1当且仅当B∈wn。

定理4.3 设Σ├╱IDA，m＊＝＜W＊，R＊，V＊＞是与Σ、A相关的三元组，wi、wj∈W＊。

［1］对所有的w、w′、w″∈W＊，wR＊w并且wR＊w′∧w′R＊w″→wR＊w″；

［2］对所有的w、w′∈W＊，wR＊w′→w⊆w′。

定理4.4 设Σ├╱IDA，m＊＝＜W＊，R＊，V＊＞是与Σ、A相关的三元组，D∈Form（LIP）。那么，对于任意的n（≥1），V＊（D，wn）＝1⇔D∈wn。

证明：

［1］当D为原子公式，则由V＊的定义可知，命题成立。

［3］当D为B∨C时。

先证B∨C∈wn⇒V＊（B∨C，wn）＝1

B∨C∈wn⇒B∈wn或者C∈wn（wn是强协调的之析取性）

⇒V＊（B，wn）＝1或者V＊（C，wn）＝1（归纳假设）

⇒V＊（B∨C，wn）＝1（语义定义）

再证V＊（B∨C，wn）＝1⇒B∨C∈wn

V＊（B∨C，wn）＝1⇒V＊（B，wn）＝1或者V＊（C，wn）＝1（语义定义）

⇒B∈wn或者C∈wn（归纳假设）

⇒B∨C∈wn（wn是强协调的之形式推演封闭性）

［4］当D为B∧C时。

先证B∧C∈wn⇒V＊（B∧C，wn）＝1

B∧C∈wn⇒B∈wn而且C∈wn（wn是强协调的之形式推演封闭性）

⇒V＊（B，wn）＝1而且V＊（C，wn）＝1（归纳假设）

⇒V＊（B∧C，wn）＝1（语义定义）

再证V＊（B∧C，wn）＝1⇒B∧C∈wn

V＊（B∧C，wn）＝1⇒V＊（B，wn）＝1而且V＊（C，wn）＝1（语义定义）

⇒B∈wn而且C∈wn（归纳假设）

⇒B∧C∈wn（wm是强协调的之形式推演封闭性）

［5］当D为B→C时。

假设V＊（D，wn）＝1：

（1）如果对于任一wm∈W，若wnRwm，则V（B，wm）＝V（C，wm），那么根据归纳假设有：B∈wm当且仅当C∈wm，因为wnRwn，所以有B∈wn当且仅当C∈wn，即或者B∈wn且C∈wn，或者B∉wn且C∉wn，亦即有或者B∈wn且C∈wn，或者 B∈wn且C∈wn。这样，或者有wn├B且wn├C或者有wn├ B且wn├ C，那么根据公理2和公理3，均可得到：wn├B→C，因为wn是强协调集，所以有（B→C）∈wn。

（2）如果对于任一wm∈W，若wnRwm，则V（B，wm）＝0，V（C，wm）＝1，且B、C相关。那么根据归纳假设有：B∉wm，C∈wm，且B、C相关，因而有 B∈wm，C∈wm，且B、C相关。因为wnRwn，所以有 B∈wn，C∈wn，且B、C相关。这样，有wn├ B，wn├C且B、C相关，那么根据公理4可以得到：wn├B→C，因为wn是强协调集，所以有（B→C）∈wn。

假设V＊（D，wn）＝0：

（1）如果存在wm∈W，wnRwm，V（B，wm）＝1，V（C，wm）＝0，根据归纳假设有：B∈wm，C∉wm。假设（B→C）∈wm，则有C∈wm，矛盾。因此可得（B→C）∉wm，因为wnRwm，所以wn⊆wm，因此（B→C）∉wn。

（2）如果存在wm∈W，wnRwm，V（B，wm）＝0，V（C，wm）＝1且A、B不相关，那么根据归纳假设有：B∉wm，C∈wm，且B、C不相关，因而有 B∈wm，C∈wm，且B、C不相关。这样，有wm├ B，wm├C且B、C不相关，那么根据公理5可以得到：wm├ （B→C），因为wn是强协调集，所以有 （B→C）∈wm，因而（B→C）∉wm，因为wnRwm，所以wn⊆wm，因此（B→C）∉wn。

定理4.5 设Σ⊆Form（LIP），A∈Form（LIP）。

［1］如果Σ是协调的，则Σ是可满足的；

［2］如果Σ╞IDA，则Σ├IDA；

［3］如果╞IDA，则├IDA。

证明：

［1］设Σ是协调的。则有A∈Form（LIP），使得Σ├╱IDA。由定理4.2可知，Σ能扩充为Σ1⊆Form（LIP），使得Σ1是强协调的并且Σ1├╱IDA，取任何B∈Σ，有B∈Σ1，由定理4.4可得V＊（B，w1）＝1，因此V＊（Σ，w1）＝1，从而Σ是可满足的。

［2］假设Σ├╱IDA，由定理4.2可知，Σ能扩充为Σ1⊆Form（LIP），使得Σ1是强协调的并且Σ1├╱IDA，取任何B∈Σ，有B∈Σ1，由定理4.4可得V＊（B，w1）＝1，因此V＊（Σ，w1）＝1，但是A∉Σ1，由定理4.4可得V＊（A，w1）＝0。所以Σ╞╱IDA。

［3］是［2］的特殊情形。

定理4.6 设Σ⊆Form（LIP），A∈Form（LIP）。

［1］Σ├ （A∧ A）

［2］├╱IDA∨ A

［3］├╱IDA→A

［4］├╱IDA∧ A→B

即在该系统中，不矛盾律仍然是定理，但是排中律、双重否定消去律、司各脱法则不是定理。因此，在该系统中，弗协调逻辑和直觉主义逻辑的基本特征都被保留了下来。由此可见，该系统给出了处理矛盾问题（包括悖论问题）［11－12］的一个直觉主义方案。

［1］ 杜国平.经典逻辑视野中的弗协调逻辑［J］.华南师范大学学报，2007（5）.

［2］ 杜国平.哲思逻辑［J］.东南大学学报：哲学社会科学版，2007（4）.

［3］ 杜国平，马亮.哲思逻辑的判定问题［J］.安徽大学学报，2007（5）.

［4］ 杜国平.知识蕴涵逻辑系统［J］.逻辑学研究，2008（2）.

［5］ 杜国平，王洪光，等.知识蕴涵模态逻辑系统［J］.徐州师范大学学报，2008（5）.

［6］ Guoping Du，Hongguang Wang，Na Li，Liang Xu.The Completeness and Decidability of Intuitive Implication Logic System［C］／／Maozu Guo，Liang Zhao，and Lipo Wang（eds.），Fourth International Conference on Natural Computation，Volume 4.Jinan，Shangdong，China，18－20Oct.2008.pp.573－577.

［7］ 杜国平.知识蕴涵时态逻辑系统［J］.安徽大学学报，2009（5）.

［8］ Hongguang Wang，Na Li，Guoping Du.Intuitive Implication Logic System［C］／／Yixin Chen，Hepu Deng，Degan Zhang，and Yingyuan Xiao（eds.），The Sixth International Conference on Fuzzy Systems and Knowledge Discovery，Vol.2，Tianjin，China，14－16Aug.2009.pp.252－256.

［9］ Guoping Du，Xiaohua Chen，Hongguang Wang.Intuitive Implication Predicate Logic System［C］／／Da Ruan，Tianrui Li，Yang Xu，Guoqing Chen，and Etienne E Kerre（eds.），The Ninth International Conference on Fuzzy Logic and Intelligent Technologies in Nuclear Science，Vol.4，Chengdu，China，2－4Aug.2010.pp.198－203.

［10］ 杜国平.可拓策略存在性研究［J］.哈尔滨工业大学学报，2006（7）.

［11］ 杜国平.集合论—泛逻辑悖论［J］.北京航空航天大学学报，2009（3）.

B81

A

1671－511X（2012）02－0018－05

2011－01－21

国家社会科学基金项目“不协调理论的推理机制研究”（10BZX054）阶段性成果。

杜国平（1965－），男，江苏盱眙人，工学、哲学双博士，中国社会科学院哲学研究所研究员，研究方向：逻辑学。