基于博弈收益共享契约的农—零供应链协调研究

曹庆奎，李青梅

（河北工程大学 经济管理学院，河北 邯郸 056038）

农产品供应链是个非常复杂的系统，它包含多个农合社、多个分销商、多个零售商等[1]。合作与竞争是供应链中各成员运营的主旋律，各成员往往以追求自身利益最大化为目标而分散决策，这会导致供应链系统出现双重边际化效应，使供应链很难达到合作时的利润水平，这就需要对供应链进行协调，通过某种契约使利润得到合理的分配，以便充分调动起各成员合作的积极性[2]。

对供应链协调的研究所采用的方法多为数量折扣、回购契约、延期支付、补货策略等，例如，Chen和Zheng认为：若不考虑价格弹性，数量折扣契约就可以协调包含多个零售商的供应链。Pasternack指出供应商、零售商及供应链系统可以通过调整回购契约的契约参数实现供应链利润的任意分配。Mosheiov等在延期支付条件下，对由一个生产商和多个零售商组成的供应链进行了协调。杨爱峰，冯帅及刘冀琼利用价格折扣和价格补贴策略对由单生产商及多零售商组成的供应链进行了协调。公彦德应用shapley值法和讨价还价能力两种形式对因合作带来的增益进行了合理的分配。本文考虑供应链各成员在合作及非合作两种情形，对由单农合社及2个零售商组成的单周期供应链应用收益共享契约对增益进行了合理分配，实现了供应链的协调。

1 基本假设及模型符号

1.1 基本假设

（1）模型中存在单一农合社和2个相互独立的零售商，研究的是销售同一产品的问题。

（2）市场需求是不确定的，且销售的产品的生命周期及销售季节都较短。

（3）农合社及零售商都是风险中性的。

（4）农合社给每个零售商的批发价格相同，零售商出售前不必再对产品进行加工。

（5）零售商1与2的边际成本相同。

1.2 模型符号

w为批发价格，是农合社的决策变量；

c为农合社的单位产品的生产成本；

pi为零售商i的销售价格，是零售商i的决策变量，i=1,2；

Di为市场需求：

α为市场的基准需求率；β消费者对价格的敏感系数；γ市场需求的扩散程度：γ＞0;βγ＜α;零售商1与2的边际成本；

k为合作后整条供应链的利润增加额。

2 供应链成员间的协调模型

本文考虑了一个单农合社及2个零售商组成的单周期供应链，供应链中的各成员都是以自我利益最大化为中心进行决策，各决策之间是相互影响的。下面分两种情况进行讨论。

2.1 非合作下农合社及零售商的决策

由于此供应链是由单农合社与2个零售商组成的，它们之间不仅存在着横向的竞争还存在纵向的竞争，如果不对各成员进行协调，那它们将进行非合作的博弈。

作为供应链主导者的农合社，以自己的利益最大化为前提，首先确定自己的批发价格，2个零售商随后根据农合社给出的批发价格，以自己利益最大化为原则，确定各自的销售价格。上述决策问题表述如下：

整条供应链的利润为：

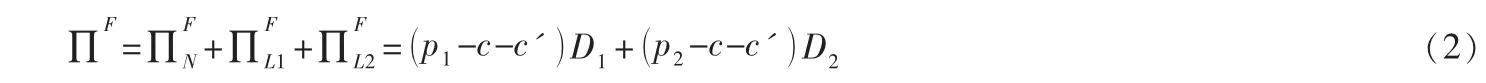
对（1）求导，得出农合社及零售商在非合作下的博弈均衡解：

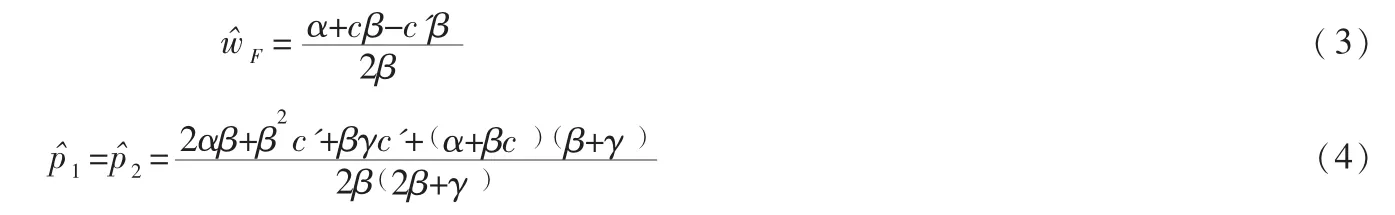
将博弈均衡解带入（1）和（2）中得到非合作下农合社及零售商的收益如下：

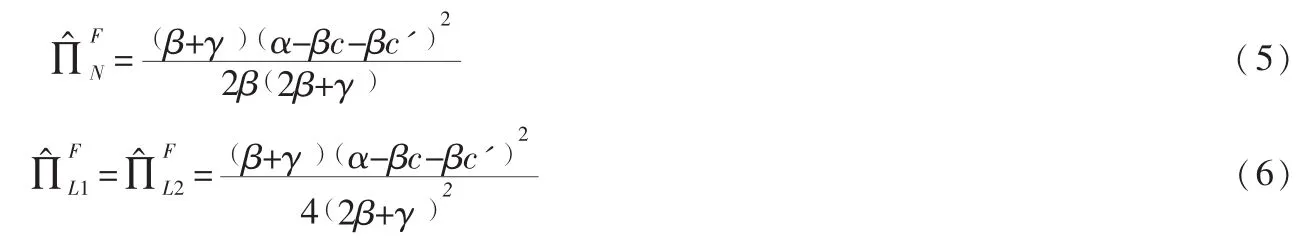
2.2 合作下农合社与零售商的决策

供应链成员之间存在着横向及纵向的竞争，如果对其进行协调，它们将放弃竞争转向合作，各个成员将分别发挥各自在生产领域及销售领域的优势，形成有效合作的体系，从而使整条供应链的利润得到优化。决策问题如下：

即：

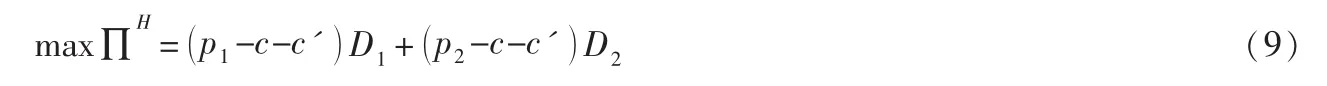
将（9）分别对p1及p2求导，并令导数为0，得：

将整条供应链的利润为：

合作后供应链的整体利润通常会增加，但对增益如何分配，是供应链中的每个成员尤其是合作反而使自己利润比不合作时减少的成员十分关注的问题，分配不合理会导致有些成员不想合作，为使所有的成员都有合作的积极性，这就需要对供应链进行协调。

2.3 供应链的协调

供应链的协调就是通过提供一些合适的信息，给予一些激励的措施，使供应链的利润得到合理的分配。即：

坤二少爷接在手中，疾速扫视一遍，不由心中一喜。他放下贴，微微一笑，说：“贵府的凶险就在这贴子之中。天机不可泄露，在下告退！”便站起身，做出要走的样子。

合作后整条供应链的利润增加额为：

假设农合社的收益共享系数为δ；零售商i的收益共享系数为χi

其具体值取决于农合社及各个零售商的讨价还价的能力，在这里用供应链各个成员在非合作时的利润占非合作时整条供应链利润的百分比表示，因为在非合作时各个成员取得的利润代表了其各自的能力，取得的利润多，其能力就强，即讨价还价的能力也就强。

即：

在分配利润时，先按非合作时各方所得的利润进行分配，以保证至少使各方得到非合作时的利润，然后再按上述规则分配增加的利润。

即合作后各方得到的利润为：

3 实证研究

3.1 实证背景

某供应链由单一农合社和两个零售商组成，农合社向两个零售商提供农产品，其处于供应链的核心地位。3者的博弈过程如下：农合社先给定一个批发价格w，零售商i根据利润最大化原则确定销售价格，此销售价格将影响市场需求，进而影响零售商的定货量，农合社再根据所有零售商的定货量，以利润最大化为前提，确定出最优的批发价，当然零售商之间也存在着博弈关系。

3.2 数据获取

通过问卷调查及专家打分获得的数据如表1所示。

表1 参数及参数值表

3.3 两种博弈下的利润

3.4 利润分配

根据（14）、 （15） 及（16） 得 K=787.25

经协调后供应链各成员的利润为：δ=0.786;χ1=χ2=0.107

显然，通过协调供应链各个成员的利润都增加了。

4 结 论

本文构建了一个由单农合社和2个零售商组成的单周期供应链模型，分析了在非合作博弈及合作博弈两种情形下的供应链各成员及供应链整体的利润情况，然后应用收益共享契约对增益进行了合理地分配，并以某地区的农零供应链为例进行了研究，进而证明了模型的有效性，对以后农企更好的合作有一定的指导意义。

[1]贾俊秀，唐奇良.单零售商和多供应商间的协调机制[J].工业工程，2008,11(6):15-19.

[2]游军，郑锦荣.农产品供应链研究进展[J].湖南农业科学，2009(10):99-102.

[3]Chen F.,Federgruen A.,Zheng Y..Coordination mechanisms for decentralized distribution systems with one supplier and multiple retailers[J].Management Science,2001,47(5):693-707.

[4]PASTERNACKB.Optimal pricing and returns policies for perishable commodities[J].Marketing Science,1985,4(2):166-176.

[5]Mosheiov G.,Sidney J B..Scheduling with general job dependent learning curves[J].European Journal of Operational Research,2003,147:665-670.

[6]杨爱峰，冯帅，刘冀琼.基于价格折扣和价格补贴的一对多供应链协调模型[J].系统管理学报，2011,20(1):109-118.

[7]公彦德.基于Shapley值和讨价还价能力的供应链协调策略[J].南京工业大学学报（社会科学版），2009,8(4):70-73.

[8]孙荣庭，孙林岩，李刚.不确定需求下多零售商竞争的供应链协调研究[J].工业工程与管理，2010,15(1):49-52.

[9]王晓立，马士华.供应和需求不确定条件下物流服务供应链能力协调研究[J].运筹与管理，2011,20(2):44-49.

[10]施国洪，于成龙，贡文伟.基于生产不确定和需求不确定的供应链协调研究[J].工业工程与管理，2011,16(2):1-4.

[11]周小明，朱云龙，尹朝万.多对一供应链收入共享契约中的采购优化[J].计算机集成制造系统，2009,15(11):2147-2152.