基于遗传算法的机抽系统优化设计新方法
2012-11-15赵瑞东熊春明张建军中国石油勘探开发研究院北京100083
赵瑞东,熊春明,张建军(中国石油勘探开发研究院,北京100083)
吴晓东(中国石油大学(北京)石油工程教育部重点实验室,北京102249)
师俊峰,朱拾东,张 娜(中国石油勘探开发研究院,北京100083)
基于遗传算法的机抽系统优化设计新方法
赵瑞东,熊春明,张建军(中国石油勘探开发研究院,北京100083)
吴晓东(中国石油大学(北京)石油工程教育部重点实验室,北京102249)
师俊峰,朱拾东,张 娜(中国石油勘探开发研究院,北京100083)
机抽系统优化设计问题属于多参数系统优化问题,参数包括冲程、冲次、泵径、平均杆径、下泵深度等。将遗传算法引入到机抽系统优化设计中,形成了一种新方法,该法采用二进制编码形式来表示抽汲参数和下泵深度,按优胜劣汰的原则来寻求问题的最优解,既能提高优化设计的速度,又能克服模糊数学以及专家系统等方法易漏掉最优方案的缺点。通过实例进行敏感性分析表明,遗传代数越多、交叉系数越高时,算法优化效果越好,而适中的变异系数有利于优化设计。
遗传算法;有杆泵;系统效率;多参数;优化设计
机抽井的优化设计主要包括抽汲参数的优选和抽油设备的选择。优化目标的复杂多样性、多个影响因素的互相关联性以及变化参数的间断性导致了设计过程的复杂性。现场新设备的引入也为优化设计方法提出了新的要求,如新型变频配电柜可对冲次进行无级调速。常见的设计方法有枚举法、专家系统以及模糊数学寻优等方法,其中专家系统和模糊数学寻优把设计者的经验融入方案的选择过程中,可能会漏掉最理想的方案;而枚举法会增大软件的运行时间,在实际操作中,将各个参数人为控制在比较小的变化范围,这同样可能会导致丢失方案,特别是设计人员经验不足时会更加突出,设计出的结果不理想[1]。
对有杆泵这种多参数系统进行优化设计时采用遗传算法,将具有优化空间大,搜索速度快,稳定性好,精度高的特性[2~4],弥补以上几种设计方法的缺点,可以引入到机抽系统优化设计中来。
1 机抽井优化设计遗传算法
1.1 基因编码
选择如下几个抽汲参数作为优化参数:下泵深度、泵径、冲程、冲次、平均杆径。用“平均杆径”这一变量取代各级杆的杆径有如下优点:一个是减少了优化参数的数目,另一个是由于不同的杆柱组合得到不同的平均杆径,使平径杆径成为连续量,有利于进行优化设计。但如果杆柱结构比较复杂,如包含加重杆、混合杆,则需要相应增加优化参数。
针对各个参数的取值特点,采用不同的编码方式。下泵深度、平均杆径、冲次可以采用平均步长的方法,将参数优化范围平均分成n段。以下泵深度为例,假设下泵深度优化范围1050~1365m,平均变化步长为5m时,n=63,则可由下式求出二进制编码的串长k=5,注意k应该取满足下式的最小值:

式中,n为分段数;k为二进制编码串长。
当下泵深度为1090m时,二进制编码表示为 {01000}。冲程、泵径等参数非连续,是具有间断性的,需要制定对应规则,将其转换为二进制编码。例如,对于冲程系列:3、4、5、6m,分别对应如下编码:00、01、10、11,此时k=2。将冲程、冲次、泵径、平均杆径以及泵深的二进制编码顺次组合到一起,就得到了一个有杆泵优化的一组编码,即遗传算法中的一个个体。
1.2 目标函数
将系统效率作为机抽系统优化设计的目标函数。当地面设备、流体参数以及井身参数给定时,系统效率只是抽汲参数的函数[5~7],即:

式中,η为系统效率,%;S为冲程,m;N为冲次,次/min;D为泵径,mm;L为泵深,m;dr为杆径,mm。
1.3 限制性条件
1)保证油井的实际产量Q不低于设计产量Qp。
2)抽油杆柱强度限制性条件为:

式中,σmax为抽油杆柱顶部的最大应力,MPa;[σmax]为抽油杆最大许用应力,MPa。
3)抽油机承载能力:

式中,Pmax为悬点最大载荷,N;[Pmax]为悬点最大许用载荷,N;Mmax为减速箱曲柄轴最大扭矩,N·m;[Mmax]为曲柄轴最大许用扭矩,N·m。
1.4 个体选择

1.5 交叉操作与变异操作
将父代中所有的个体,进行两两交叉。如图1所示,需要随机选定一个位置作为交叉点,将2个个体划分成2部分,相互交换后半部分,分别得到2个新的个体。
从父代中随机选择个体进行变异操作。如图2所示,选定一个随机位置,翻转该位置的二进制字符,从而得到一个新样本。

图1 交叉操作示意图
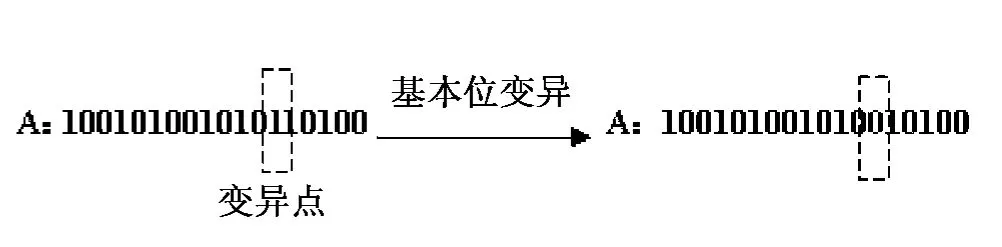
图2 变异操作示意图
1.6 遗传算法优化流程
遗传算法优化流程如下:①给定机抽系统各生产参数的取值范围,确立编码方案。②生成初始种群——采用二进制编码对参数区间内的各参数进行编码,随机生成M个个体,每个个体的二进制数位数由优化参数数目和变化步长决定。③遗传操作——对初始种群以指定的选择方法进行选择,按确定的交叉概率进行交叉,依稳定的变异概率实施变异,生成过渡种群。④对过渡种群中各个个体进行解码。⑤对解码后的每个个体,分别调用机抽系统优化设计软件进行个体评价,得到个体适应度。⑥判断遗传运算是否满足精度,“是”则保存最优值退出;“否”则返回第③步继续进行运算。
2 变异系数和交叉系数的优选
在遗传算法中,优选变异系数和交叉系数有利于提高整个算法的精度和速度,为此选择不同的交叉系数和变异系数,利用上述方法对某有杆泵抽油井进行优化设计。从表1中可以看出,循环代数越多、交叉系数越高,算法优化效果越好,而采用适中(比如0.05)的变异系数有利于优化设计。
3 设计实例
利用该设计方法对某井进行生产参数优化设计,并与常规优化结果进行了对比。基础数据:抽油机型号CYJ12-4.2-73HB,生产气油比20m3/m3,原油相对密度0.85,油压0.5MPa,套压0.5MPa,油层中深2000m,地层静压为23MPa,无气锚。以系统效率最高作为目标函数进行优化设计。优化参数及其变化范围见表2,理论上,一共有160万(4×50×4×20×100)种参数组合,如果采用枚举法,运行时间将非常长,这在实际应用中很难实现。利用遗传算法进行优化时,设每一代包含10个个体,交叉系数为0.7,变异系数为0.04,其优化结果如图3所示。
从图3中可以看出,平均系统效率和最大系统效率随着代数的不断增加呈上升趋势,当循环到第15代时,系统效率从初始的19.4%增加到22.7%,表明遗传操作在优化过程中起到了作用,寻优速度非常快。采用遗传算法进行优化设计的结果与常规设计法基本一致,前者相比模糊数学寻优和专家系统方法扩展了搜索空间,相比枚举法大大提高了优化速度,表现了其明显的优化效果。

表1 不同遗传参数组合的标准偏差表

表2 优化参数表

图3 遗传算法优化结果图
4 结 论
1)提出利用遗传算法进行有杆泵抽油系统优化设计的新方法。该法采用二进制编码形式来表示抽汲参数和下泵深度,按优胜劣汰的原则来寻求问题的最优解。
2)通过实例进行敏感性分析表明,遗传代数越多、交叉系数越高时,算法优化效果越好,而采用适中(比如0.05)的变异系数有利于优化设计。
3)基于遗传算法的优化设计方法相比模糊数学寻优和专家系统方法扩展了搜索空间,相比枚举法大大提高了优化速度,具有明显的优化效果。
[1]张琪.采油工程原理与设计[M].北京:石油大学出版社,2003.
[2]高松竹.用改进遗传算法解压气站优化运行问题[J].天然气与石油,2003,21(3):17~19.
[3]邓勇,刘志斌,陆燕妮.自适应遗传算法在气田开发规划产量分配优化模型中的应用[J].大庆石油地质与开发,2006,25(3):45~47.
[4]蒋明,仲颖,王亚洲.用遗传算法求解油藏动态预测的非线性模型[J].大庆石油地质与开发,1999,18(6)18~20.
[5]孙庆宇.有杆泵井机采系统效率影响因素及参数优化设计[J].油气田地面工程,2004,23(6):52.
[6]金明权.定向井有杆泵优化设计技术研究[J].石油工程建设,2005,31(z1):1~5.
[7]冯虎,吴晓东.有杆抽油系统井下能耗研究[J].石油钻采工艺,2005,27(6):63~65.
Genetic Algorithm-based Optimizing Design for Rod Pumping System
ZHAO Rui-dong,XIONG Chun-ming,ZHANG Jian-jun,WU Xiao-dong,SHI Jun-feng,ZHU Shi-dong,ZHANG Na(First Author's Address:Research Institute of Petroleum Exploration and Development,CNPC,Beijing100083,China)
Genetic algorithm had very big space for optimization,powerful global search ability,high precision,strong robustness for optimization of multi-parameter system.Rod pumping optimization belonged to multi-parameter optimization,which included stroke,strokes per minute,pump diameter,average rod diameter and depth of pump.A new method was developed by introducing the genetic algorithm into the rod pumping optimization design.In the method,a binary encoding was deployed to present swabbing parameters and depth of pump for avoiding the shortcomings of omissions in fuzzy mathematics and expert system for achieving minimum system efficiency and optimal solution.The results show that genetic algorithm-based optimal designs have good optimization results and certain practical value.
genetic algorithm;rod pumping;system efficiency;multi-parameter;optimal design
TE933.02
A
1000-9752(2012)06-0158-03
2012-02-10
中国石油天然气股份有限公司科学研究与技术开发项目(2011B-1708)。
赵瑞东(1980-),男,2002年大庆石油学院毕业,博士,工程师,现从事油气田开发方面的研究。
[编辑] 萧 雨
