Mathematica 8.0.1中文版在量子力学教学中的应用

单传家, 陈入云,刘继兵,陈 涛,刘堂昆,黄燕霞

(1.湖北师范学院 物理与电子科学学院，湖北 黄石 435002;2.湖北师范学院 外国语学院，湖北 黄石 435002)

0 引言

Mathematica[1]是美国Wolfrmn公司研制开发的著名数学计算软件系统，很好地结合了数值和符号计算引擎、图形系统、编程语言、文本系统、和与其他应用程序的高级连接。自1987年发布系统的1.0版本开始便迅速广为流传，后经不断改进和完善，1991年与1997年又先后推出2.0版和3.0版，1999年推出4.0版本，后来推出了5.0(2003)，6.0(2007)，7.0(2008)，直到2011年推出了8.0中文汉化版本。该版本增加了500多个新函数，功能涵盖更多应用领域，并拥有更友好更高质量的中文用户界面、中文参考资料中心及数以万计的中文互动实例，使中国用户学习和使用 Mathematica 更加方便快捷。自从20世纪60年代以来，在数值、代数、图形、和其它方面应用广泛。Mathematica是世界上通用计算系统中最强大的系统，现在，它已经被应用于科学的各个领域——物理、生物、社会学、和其它[2～5]。

量子力学[6～7]是研究微观粒子的运动规律的物理学分支学科，它主要研究原子、分子、凝聚态物质，以及原子核和基本粒子的结构、性质的基础理论，它与相对论一起构成了现代物理学的理论基础。量子力学的基本原理包括量子态的概念，运动方程、理论概念和观测物理量之间的对应规则和物理原理。量子力学的理论框架是由下列五个假设构成的：1)微观体系的运动状态由相应的归一化波函数描述。2)微观体系的运动状态波函数随时间变化的规律遵从薛定谔方程。3)力学量由相应的线性算符表示。4)力学量算符之间有想确定的对易关系，称为量子条件；坐标算符的三个直角坐标系分量与动量算符的三个直角坐标系分量之间的对易关系称为基本量子条件；力学量算符由其相应的量子条件确定。5)全同的多粒子体系的波函数对于任意一对粒子交换而言具有对称性：玻色子系的波函数是对称的，费米子系的波函数是反对称的。

本文我们首先通过一些例子简单的介绍了Mathematica系统简单操作与功能，然后重点介绍了Mathematica 8.0.1中文版在量子力学教学中的应用，包括包括如何用久期方程求解本证值和本证波函数，如何根据薛定谔方程求解波函数态矢量的演化。通过举例可以清晰的看到利用Mathematica 8可以很容易的求解上述的量子力学问题。

1 Mathematica系统简单操作与功能介绍

1.1 进入系统与退出系统

在“开始”菜单的“程序”中单击Mathematica 8.0选项进入系统，在屏幕上显示一个工作窗口，并将这个窗口暂命名为Untitled-1.退出Mathematica系统时，只须单击工作窗口右上方的关闭按钮，或者选择菜单“file/ Exit”，或者按“Alt+F4”键。

1.2 工作窗口操作

工作窗口是用户输入、输出、显示各种信息，以及运行各种程序的场地，用户的全部操作都将在这里进行，人们将这种类型的窗口称之为Notebook。下面举例说明在工作窗口中怎样进行操作。

例1-1已知a=2，b=3.7，试求c=a+b的值。

在Untitled-1工作窗口中直接键入：a=2;b= 3.7;c=a+b，然后按执行键(执行键：Shift+Enter，或右Shift)，执行后，显示结果如下：Out[1]: 5.7

例1-2已知函数y=sinx，试求其一阶导函数y'.

在工作窗口中键入：y' = D[Sin[x],x] 执行结果为：Cos[x]

例1-3画出函数y=sinx在区间[- 3，3]上的图形。

在工作窗口中键入：Plot[Sin[x], {x, -3, 3}]，出现结果如图1：

图1 工作窗口显示图

注意：在Mathematica中函数名或者命令的第一个字母均必须大写，其具体内容将在后面的“函数名的书写规则”中作严格的规定。

1.3 建立文件与保存文件

在工作窗口做好的某些内容，如果想要保留，以供今后多次使用，通常是建立一个新文件，将做好的内容保存在文件中。保存文件的方法是：选择菜单“File/Save”或“File/Save As”，然后在对话框中操作。如此保存的Mathematica文件的扩展名为.nb，其中保存有Notebook中所有输入文字与输出的文字和图形。调出文件，选择菜单“File/Open”，在对话框中操作，选择文件名后单击“打开”按钮即可，在屏幕上便可看到重新调出的文件中的文字与图形了。

1.4 Mathematica功能介绍

开始使用Mathematica时，不必担心是否能够学会，其实它就像使用电子计算器一样简单。而要做的主要事情就是如何用Mathematica的语言来描述所要作的计算。 在很多情况下，会发现这种语言和在数学中、在一般的计算机语言中的习惯很接近。几乎人人用过计算器，它能进行+、-、*、/四则运算和简单的函数运算。Mathematica作为一个功能强大的数学软件包，在处理数值运算方面具有非常强大的功能。 使用Mathematica作数值计算就像使用电子计算器一样简单。一切命令都可以在帮助中找到，其中包括Mathematica 基本运算，常用数学函数，数值设定，常用处理代数的指令，多项式/分式转换的函数，解方程式的根，函数的定义、查询，积分微分，求极限，基本的绘图命令等等。例如：

1.4.1 微积分

Integrate[x∧2 Sin[x]∧2, x] D[%, x] Simplify[%]

ln[2]=Integrate[x∧2Sin[x]∧2,x]

D[%,x]

Simplify[%]

Out[4]=x2Sin[x]2

1.4.2 代数式运算

Mathematica还可以作代数式的各种运算：9 (2 + x) (x + y)+(x + y)∧2

将上式展开：Expand[%∧3]

In[1]=9(2+x)(x+y)+(x+y)∧2

Expand[%∧3]

Out[2]=5832x3+9720x4+5400x5+1000x6+17496x2y+30132x3y+17280x4y+3300x5y+17497xy2+32076x2y2+19494x3y2+3930x4y2+5832y3+12636xy3+

8802x2y3+1991x3y3+972y4+1242xy4+393x2y4+54y5+33xy5+y6

1.4.3 解方程或方程组

In： Solve[x∧2+y∧2==1&&x+y==a,{x,y}]

1.4.4 矩阵

m = Table[i/(i+j+1),{i, 3}, {j, 3}],MatrixForm[%] Transpose[m] Inverse[m]

Eigenvalues[N[m]]

In[14]=m=Table[i/(i+j+1),(i,3),(j,3)]

MatrixForm[%]

Transpose[m]

Inverse[m]

Eigenvalues[N[m]]

Out[17]={{300,-450,210},{-900,1440,-700},{630,-1050,525}}

Out[18]={1,1301,0.0313529,0.000447984}

2 Mathematica在量子力学课程中的应用

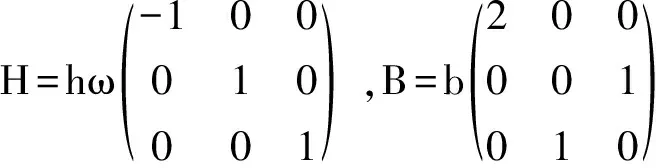
其中ω和b为实常数，问

1)H和B是否是厄密矩阵；

2)H和B是否对易；

Mathematica 代码如下：

H=h× ω×(_{ {-1, 0, 0},{0, 1, 0},{0, 0, 1} }_);

B=b×(_{{2, 0, 0},{0, 0, 1},{0, 1, 0}}_);

HermitianMatrixQ[H]

HermitianMatrixQ[B]

H.B-B.H

Eigenvalues[B]

Eigenvectors[B]

运行结果如下：

HermitianMatrix0[H]

HermitianMatrix0[B]

H.B-B.H

Eigenvalues[B]

Eigenvectors[B]

Out[17]=False

Out[18]=False

Out[19]={{0,0,0},{0,0,0},{0,0,0}}

Out[20]={-b,b,2b}

Out[21]={{0,-1,1},{0,1,1},{1,0,0}}

从上面的结果我们可以看出，H和B都不是厄米矩阵，H和B是对易的，直接可以求出B的本征值和本征态。

假设Ψ(0)=|↑↓〉，时间t演化为Ψ(t)=C1↑↑〉+C2|↑↓〉+C3|↓↑〉+C4|↓↓〉

H=J×KroneckerProduct[σ1,σ2].a//MatrixForn

c1[0]==0,c2[0]==1,c3[0]==0,c4[0]==0},{c1[t],c2[t],c3[t],c4[t]},t]

从上面的程序就可以看出态演化的结果。

3 结论

Mathematica在量子力学中的应用是很广泛的, 通过Mathematica 8.01数值软件对量子力学中的两个简单的例子进行了研究，结果表明，Mathematica 8.01在量子力学问题处理中发挥着很重要的作用，需要大量手工推导的解析计算, 都可以借助Mathematica来完成, 从而大幅度地提高工作效率和工作质量。Mathematica 8.01在其他学科中的作用我们将做进一步的研究和探讨。

参考文献:

[1]Wolfram S.MATHEMATICA[M].赫孝良,周义仓，译.西安:西安交通大学出版社, 2002.

[2]王立志,阮文举,柳盛典,等.Mathematica处理量子谐振子[J].德州学院学报，2007, (2): 7～9.

[3]李泽涛,黄双林.基于Mathematica 5.0的夸克-反夸克束缚态薛定谔方程的数值解法[J].西南师范大学学报(自然科学版), 2010,35(4): 43～47.

[4]易秀英, 王三宝.Mathematica的中心极限定理的实验分析[J].黄石理工学院学报, 2010, 26(1): 29～32.

[5]陈显盈, 尤爱惠.用Mathematica演示波的衍射干涉现象[J].物理通报, 2010,(11): 95～96.

[6]周世勋.量子力学[M].北京: 高等教育出版社，1979.

[7]曾谨言.量子力学[M] .北京: 科学出版社, 1999.