数学思想在化学解题中的应用
2012-11-15钱春
钱 春
徐州生物工程职业技术学院生物工程系,江苏 徐州 221006
数学思想在化学解题中的应用
钱 春
徐州生物工程职业技术学院生物工程系,江苏 徐州 221006
数学是工具学科,是学习化学的基础,在化学解题中渗透数学思想方法,有助于培养学生的思维能力,拓宽学生的视野,提高学生发现问题,分析问题,解决问题的能力。
数学思想;化学解题;应用
前言
数学思想是对数学知识与方法本质的概括,是数学各部分知识联系的纽带。将化学问题抽象成数学问题,利用数学工具,通过计算(结合化学知识),解决化学问题,是发展化学思想能力的重要途径之一。现在分类示例,谈谈如何应用数学思想方法,培养学生解决化学问题的能力。
1 数学模型思想的应用
数学是学习化学的工具,在化学学习中,有些概念与概念之间,物质与物质之间的相互转化关系 用化学语言来描述显得十分繁琐,若通过分析后转换成数学模型,则相互间的关系就显得十分清楚。数学模型是思想模型的一个较高层次,将具体的化学问题转化成数学模型需要进行一系列的观察、分析、综合等思维能力,这种思维方式的应用有利于提高学生的抽象思维的能力。
构建数学模型解决化学问题一般可按如下步骤进行:
1.1 查清问题的基本情况,分析问题所涉及的各种量,弄清那些是常量?那些是变量?那些是已知量?那些是未知量?
1.2 分析所研究系统的关系结构,即根据实际问题的特定和具体要求考虑主要因素和有关量之间的关系。
1.3 进行抽象概括。即抽象出事物系统所含诸对象之间的主要关系,利用有关的数学理论和数学语言来刻画这种关系。
常见的数学模型可以分为三种:概念型模型,方法型模型,结构型模型,这里我们将重点介绍方法型模型中的数列模型。
数列模型适用于解决一些循环往复的过程问题及有机物的一系列问题.只有恰当运用这些模型,才会达到事半功倍的效果。如:
例1.工业上用水吸收NO2制HNO3,生成的气体经过多次氧化吸收的循环操作,使其充分转化成硝酸(假定上述过程无其他损失)。(1)试写出上述反应的化学方程式。(2)假设循环操作的次数为n, 试写出NO2转化成硝酸转化率与循环操作次数n之间 的数学表达式。(3)计算一定量的二氧化氮气体要经过多少次循环操作,才能使95%的二氧化氮转化成硝酸?
解析:本题是一道工业制硝酸的习题,他考察了硝酸工业生产过程最后一步,二氧化氮与水反应生产硝酸。而1mol二氧化氮被水吸收有1/3mol NO产生,NO继续被氧气氧化生成二氧化氮。然后再进一步吸收往复循环直至完全吸收为止。
由反应方程式3NO2+H2O==2HNO3+NO和2NO+O2==2NO2,我们不难发现,每经过一次循环,生成的硝酸的物质的量构成一个等比数列,其首项为2/3,公比为1/3,而第n次循环所生成的硝酸的物质的量应为这个等比数列的前n项之和。

故二氧化氮转化成硝酸的转化率为{1-(1/3)n/1}*100%
当二氧化氮的转化率为95%时,{1-(1/3)n/1}*100%=95%解之得:n=2.6(次)所以,需要三次循环操作才能使95%的二氧化氮转化成硝酸 。
由上例可以看出,数学模型思想在化学教学中应用十分广泛,一个概念,一条定律,一种反应模型,一个假设体系,一个数学公式等都可以形成一个数学思想模型,思想模型的建立能使学生突破感官和时空的局限,充分发挥他们的想象和推理能力,应用这种思维方式可以拓宽学生的思维领域,从而提高学生发现问题,分析问题,思考问题的能力。
2 数形结合思想的应用
数形结合是研究化学问题时由数思形,由形思数,数形结合考虑问题的一种方法。由于现实世界本身是兼备数与形两种属性,当数学发展到一定阶段是必须将数与形结合起来,运用数形结合的方法研究化学问题具有重要的指导意义。
例2.在100ml,1mol/l的AlCl3溶液中加入100ml某未知浓度的NaOH溶液,结果产生3.9克沉淀,则加入的NaOH的浓度可能是( )
A.1.5mol B.2mol
C.2.5mol D.3.5mol
解析:AlCl3与NaOH发生的反应是:
3NaOH + AlCl3== Al(OH)3↓ + 3NaCl
Al(OH)3+ NaOH == NaAlO2+ 2H2O
以加入的 NaOH的物质的量为横坐标(单位:mol),以沉淀Al(OH)3的质量(单位:g)为纵坐标建立坐标系,如图1:

图1
从图1不难看出,只要产生的沉淀不是最大值,答案就不唯一,题中AlCl3的量为0.1mol根据0.1mol AlCl3与NaOH最多能产生0.1mol Al(OH)3沉淀,即7.8克。从图2中很容易得出n1=0.15mol,n2=0.35mol,所以答案为AD。

图2
我们在化学解题中运用数形结合能收到简洁,快速,直观的效果。因此,我们在教学中把数形结合起来便于深刻理解化学知识,从心理学的角度就是直观与抽象,感知与思维的结合,可以拓宽思路,开阔视野,使学生的思维得以深化,有利于培养学生思维的严密性。
3 化归与转化思想的应用
化归是数学研究问题的一般方法和解决问题的一般策略,因此我们可以作为一种指导思想渗透到化学解题中。根据具体内容,通过渗透、介绍、强调等不同的方式让学生体验这一思想方法。解题时,一般总是考虑将比较陌生的知识化归成以前学过的,比较熟悉的;将解题过程比较复杂的划归成比较简单的;将难度较大的划归成难度相对较小的。
3.1 过程转化、化繁为简
例3. 14克铜银合金与足量浓度的硝酸反应,将放出的气体与0.05mol的O2通过水中,恰好全部被吸收,则合金中铜的物质的量为多少?
解析:此题的过程比较复杂,通过分析可以简化为:
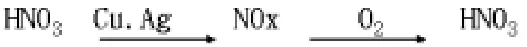
这样整个过程相当于铜银合金失去的电子间接的转移给了氧气,根据得失电子守恒可以有2ncu+nAg=0.05×4 ① 又根据质量守恒有64 ncu+108 nAg=14 ②
解得:ncu=0.05mol
3.2 角度转化、化难为易
例4.某KOH的样品中含H2O为7.62%,含K2CO3为2.38%,含KOH为90%,将1.00克样品加入到46mL,1mol/LHCl中,过量的酸用1.07mol/L的KOH溶液27.65mL恰好中和,试问将溶液蒸干得固体多少克?
解析:如果顺着试题设计者的牵引去解题,本题涉及的化学方程式较多,计算量大,难度较高,但我们如果另辟巧劲,把视角投向溶液的成分,就会发现溶液中只有KCl一种溶质,且nKCl=nCl=nHCl,得mKCl=46.00×10-3×1×74.5=3.43(g)
由以上几例可以看出,化归与转化思想的应用可以教会学生由此及彼,灵活运用所学知识,使学生的学习从无序到有序,把复杂的问题转化成简单的问题,把未知的问题转化成已知的问题,培养学生思维的深刻性。
总之,在化学解题中渗透数学思想能有效的开发学生的智力,培养和训练学生在学习新知识时的科学态度和科学方法,有利于学生的解题以及智力因素和思想因素的提高 。
10.3969/j.issn.1001-8972.2012.23.117
钱春.本科,学士,讲师,化学。
