基坑监测中三角高程替代二等水准的探讨

高绍伟，高继晶，颜 亮

(1.北京工业职业技术学院，北京100042;2.中兵勘察设计研究院，北京100053)

基坑监测中三角高程替代二等水准的探讨

高绍伟1，高继晶2，颜 亮2

(1.北京工业职业技术学院，北京100042;2.中兵勘察设计研究院，北京100053)

提出无仪器高、无棱镜高三角高程测量方法，对基坑垂直位移变形监测中三角高程测量替代二等水准测量进行了公式改正和误差分析，并通过工程案例进行验证。实践证明，在一定的监测范围内，三角高程测量可以替代二等水准测量。

无仪器高;无棱镜高三角高程测量;三角高程改正;误差分析

一、前 言

基坑的垂直位移监测一直以来采用精密几何水准的方法进行，该方法不仅作业效率低，而且受施工现场环境条件的制约比较大。随着具有自动目标识别的伺服全站仪的问世，测量手段及方法发生了革命性变化。目前，运用伺服全站仪的自动搜索照准功能进行测量，在平面上完全能够满足一定的精度要求，这在很多工程中得到了验证。然而，运用ATR功能进行三角高程测量能否达到二等或二等以上的几何水准精度，成果的可靠性如何，一直是测绘界广泛关注的问题。对于利用全站仪进行精密三角高程能否替代二等水准的问题，文献［1-4］都从不同的方面进行了研究。本文利用索佳NET05全站仪在对基坑水平监测的同时，对利用监测点的精密三角高程测量替代二等水准测量进行了探讨。

二、三角高程测量的原理

三角高程测量是根据由测站向照准点所测得的平距和垂直角，运用三角公式计算两点的高差。如图1所示，S0为A、B两点间的实地水平距离，仪器置于A点;i1为仪器高;v2为B点觇标高;δ12为观测的垂直角;R为AB方向上的椭球曲率半径。

式(1)是单向观测计算三角高程的基本公式。对式(1)进行微分，不考虑HA的误差，则高差中误差为(省去下角标)

由式(2)可以看出，影响三角高程测量的因素是测距误差ms、垂直角观测误差mδ、仪器高量测误差mi、目标高量测误差mv、大气折光误差mk。

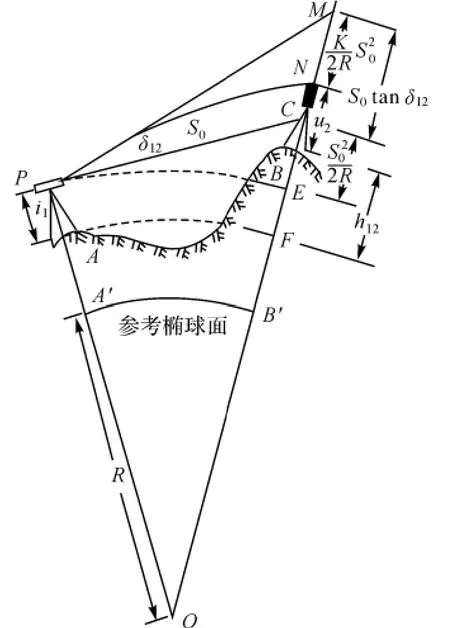
图1 三角高程测量原理

三、基坑垂直位移变形监测中三角高程测量替代二等水准测量的理论分析

1.无仪器高、无棱镜高三角高程测量方法的提出随着电子测量仪器的发展和普及，目前大多数建筑物基坑位移的监测利用全站仪采用极坐标的方法进行。当测站上有多个监测点时，对每个监测点都可以写出式(1)的公式。在式(1)中设

由式(4)可知，只要知道H0、C值就可计算出各监测点的三角高程。在观测中不需要量取仪器高和觇标高，为此也称无仪器高、无棱镜高法。

2.H0、C值的求得

为了求H0、C值，在进行监测时，首先利用精密几何水准测量的方法，按垂直位移监测的二等的指标，在基坑的周边施测3～4个点作为基准点(也可选用监测点)。现假设3个基准点分别用1、2、3表示，监测中的大气折光系数是一常数。根据式(4)各基准点的三角高程为

式中，hoi=Soitan δoi(i=1，2，3)

假设3个基准点的水准高程无误差，式(5)计算的三角高程改正数分别为V1、V2、V3，进一步写为

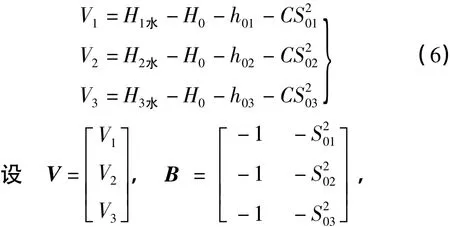
按最小二乘原理可求得［7］

最后根据式(8)就可以计算出H0、C值。再根据式(4)计算出各监测点经改正后的水准高程。

3.工程案例

图2是某一基坑监测点布置的平面示意图。基坑东西长62 m，南北长26 m，共布设了12个监测点。基坑边坡场地狭小，且周围有围挡，垂直位移监测时，立水准尺相对困难。监测点标志埋设统一加工尺寸、高度一致的标杆，在其上采用插入式觇牌安放棱镜。为了分析，先对所有监测点实施二等水准观测，经平差计算的水准高程见表1，水平位移监测两个测回。表1是监测第9期经整理的外业监测数据。

图2 基坑监测点位置示意图

表1 第9期经整理的外业监测数据m

利用G4、G5、G6的水准高程和监测的水平距离组成B和L矩阵。

解算的结果

将H0和C代入式(4)，计算结果如表2所示。

《工程测量规范》(GB/JGJ 8—2007)中［6］规定:当垂直位移采用二等变形监测时，变形观测点的高程中误差m=±0.5 mm，任意两点的高差中误差为其差值的限差为±1.41 mm。从表2可以看出G1最大差值为1.77 mm、G10为1.5 mm，其余点多满足二等的限差要求。经现场调查分析，是因为两点插入觇牌时的深度所造成的。因此可以得出结论:对经改正计算的三角高程和二等水准测量高程进行比较，若二者的差值在±1.41 mm以内，则用全站仪监测的三角高程可以满足二等水准 监测的要求。

表2 计算改正后的三角高程和水准高程数据对比 mm

4.基坑监测范围的确定

为了分析问题简化，假设计算的H0和C无误差，结合式(4)根据误差传播率得

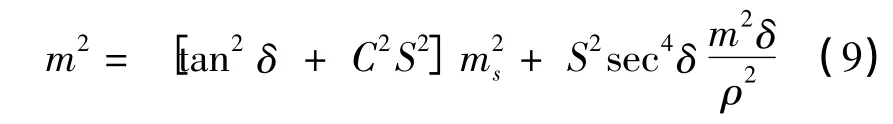
监测使用的索佳NET05电子全站仪的测距精度为±(1 mm+1×10－6D)，测角中误差为±0.5″。分别以不同的距离和垂直角组合计算对三角高程的影响如表3所示。C值使用案例的C(－1.794E-07)值。

表3 距离和垂直角对三角高程的影响 mm

从表3可以看出，监测点精度随着距离和垂直角的增大而逐渐下降。当监测的距离为150 m、垂直角最大为15°时，误差小于0.5 mm，基本能达到二等水准的精度要求。

四、结束语

本文在利用索佳NET05智能型全站仪进行基坑水平位移监测的同时，对利用三角高程替代二等水准测量进行基坑垂直位移监测等也作了研究，试图为工程监测寻找出一种既经济方便，又能满足监测精度要求的方法。

在监测时，为提高监测的精度，需采取下列措施:

1)尽量使用高精度的智能全站仪，可以减少人为照准误差，提高观测的精度。

2)当条件允许时，最好在基坑的周边选择3个以上固定的基准点，在每次监测时，只需照准即可。

3)多站监测时，不同测站的数据，需分别计算。为了检核，至少需要同时观测1个公共监测点来完成。

总之，该方法的提出，可以减少外业的监测时间，提高工作效率。特别适用于基坑狭窄、基坑周围有围挡、人员立水准尺很困难的场地。

［1］ 郭春喜，阳海峰.精密三角高程替代二等水准的可行性研究［J］.测绘信息工程，2010，(35)2:42-43.

［2］ 张正禄，邓勇，罗长林，等.精密三角高程代替一等水准测量的研究［J］.武汉大学学报:信息科学版，2006，36(1):5-8.

［3］ 周水渠.精密三角高程测量代替二等水准测量的尝试［J］.技术应用，1999(No.3).24-28.

［4］ 晏红波，黄腾，邓标.智能全站仪精密三角高程测量替代二等水准测量［J］.水电自动化与大坝监测，2007，31(4):43-47.

［5］ 陶海生.全站仪应用于高程测量之精度探讨［J］.中南公路工程，2003，28(3):59-60.

［6］ 建设部综合勘察研究设计院.JGJ 8—2007建筑变形测量规范［S］.北京:中国建筑工业出版社，2007.

［7］ 武汉测绘科技大学测量平差教研室.测量平差基础［M］.3版.北京:测绘出版社，1996.

On Attempting to Replace Second-order Levelling with Triangulated Height in the Foundation Pit

GAO Shaowei，GAO Jijing，YAN Liang

0494-0911(2012)08-0055-03

P224.2

B

2012-03-20

2011年北京工业职业技术学院科研基金(Ky201013)

高绍伟(1962—)，男，北京人，硕士，高级工程师，主要从事变形监测教学和3S技术的研究工作。