地层记录中旋回层序界面的识别方法及原理①
2012-11-13伊海生
伊海生
(1.成都理工大学沉积地质研究院 成都 610059;2.油气藏地质及开发工程国家重点实验室 成都 610059)
0 引言
频谱分析是旋回地层学研究中识别地层韵律和沉积旋回周期信号一个常用的方法,通过沉积旋回波长与米兰科维奇天文周期之间的对比关系,可以为我们了解地层旋回产生的驱动机制、建立高分辨率的年代地层格架提供一个途径[1,2]。在旋回地层研究中应用频谱分析技术鉴别米兰科维奇旋回,必须具备二个前提条件:其一,按一定的地层间隔系统测量能反映地层节律变化的参数,建立深度点对应的数字指标数据系列。例如,在深海钻探研究中一般采用有孔虫δ18O和δ13C作为气候变化的数字指标,在陆地地层剖面中可以通过测量磁化率、自然伽马、碳酸盐含量、颜色色度作为沉积旋回的定量参数[3]。其二,根据生物地层、磁性地层控制节点,通过节点之间地层间隔的时间长度计算沉积速率,将深度域数据系列转换为时间域数据系列,通过频谱分析方法检测沉积旋回的时间周期[4]。目前的问题是,在地层记录中要识别千年级米兰科维奇旋回的高频信号,必须要有高精度年代地层控制的剖面和钻井,分段计算沉积速率,才能进行深度域与时间域之间的转换,一般的地层剖面很难达到这一要求,这是旋回地层研究受到制约和局限的一个重要原因。
沉积速率是旋回地层学研究中的一个关键参数,它具有明显的随着时间和空间变化的特点。根据数字模拟实验,本文详细地论证了沉积速率变化对沉积旋回波长的影响,提出采用测井数据的频谱分析技术,可以有效地鉴别地层间断面和沉积体制转换面,标定旋回层序界面的位置。
1 旋回层序周期和波长的检测
频谱分析是通过对深度域或时间域观测的数据序列进行数学变换,求取周期信号一个常用的方法。当旋回信号变化的坐标系以时间为单位时,根据频谱分析可检测到信号波动的频率值,频率取倒数即为旋回周期。如果信号变化数据系列采用深度单位表示,则通过频谱分析求解的频率值的倒数为旋回波长。
Postma等[5]发现地层记录的伽马射线强度(GR)与日照量变化幅度可以对比,二者之间具有同步相关变化的特点,而日照量变化严格受米兰科维奇天文周期控制。兹以Laskar等[6]的日照量数据序列作为自然伽玛测井曲线的替代参数,通过对时间域和深度域数据系列的频谱分析,说明从测井数据中提取高频和低频旋回信号的处理流程和方法。
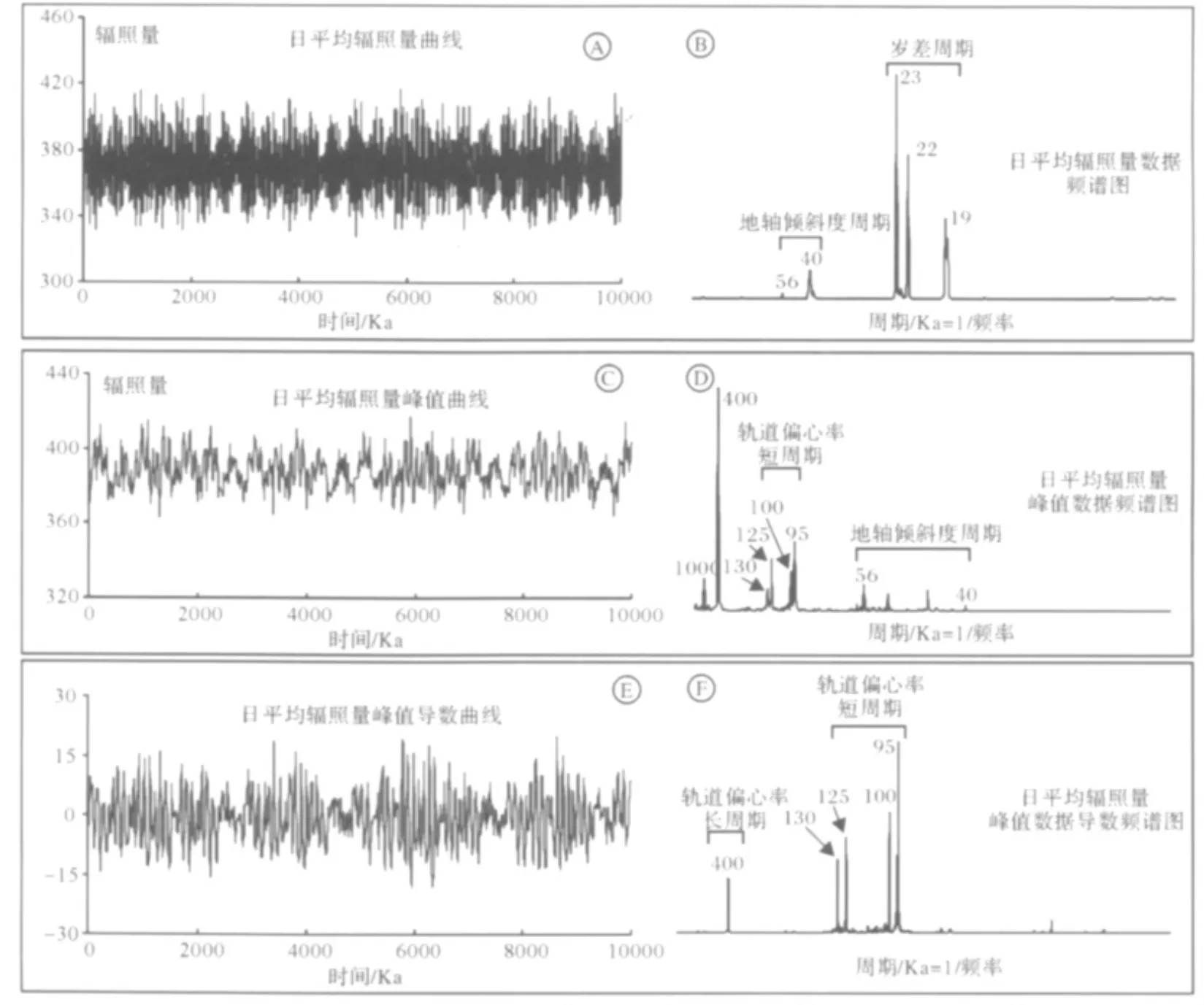
图1 频谱分析在原始日照量时间数据序列、极值日照量数据系列和经过一阶导数处理的极值日照量数据系列中检测频谱峰和周期Fig.1 The frequency peaks and periods are detected by spectrogram analysis in original insolation series,extreme point series extracted from original insolation data and processing extreme point series treated by first derivative order
图1A是距今10 Ma以来日照量变化曲线投影图。横坐标是时间单位,数据点间距1 ka,共计有数据点10 000个;纵坐标为北纬65°夏季到秋季(6~9月)平均日照量数据投影曲线,太阳常数取值为1 356 w/m2。采用 AnalySeries软件进行频谱分析[7],调用Peiodogram程序,Welch窗口,结果如图1B所示。图1B显示日照量在高频带 0.043、0.045和0.052频率点出现3个强振幅的频谱峰,根据频率与波长之间为倒数关系进行换算,则可以求得23 ka、22 ka和19 ka的岁差周期。低振幅的56 ka和40 ka周期频谱峰,对应地轴倾斜度周期。
在日照量数据的时间序列中,提取日照量数据转换点的数值,即采集日照量变化曲线波峰高点数值,可建立一个峰值点日照量随时间变化的数据序列,对数据序列进行线性等间距内插计算,求得数据点间距为21.4 ka,采用同一流程进行频谱周期分析,则可以检测到调控高频岁差旋回的偏心率周期,结果如图1C和图1D所示。从图中1D可见,在日照量峰值数据系列频谱分析图中,高频岁差周期的谱峰消失,轨道偏心率长周期400 ka谱峰显示最为明显,同时也可以检测到130~95 ka的4个轨道偏心率短周期,低频带1 000 ka超长周期也有显示。
测井曲线具有等间距采样的特点,而且数据序列连续、纵向分辨率高,因此,它可以满足数学含义上频谱分析的要求。研究表明,以时间单位标定的测井数据系列,自然伽马强度的变化可以记录米兰科维奇旋回周期[8,9]。但以深度刻度的测井数据系列中检测到的频谱峰,反映的是岩性或物性旋回的波长大小在深度坐标系的变化。以GR测井曲线为例,一般GR高值对应泥岩,低值对应砂岩和灰岩。通过提取测井曲线高点建立的极值数据系列,它检测的频谱峰,反映的是在深度坐标系泥岩—砂岩或泥岩—灰岩旋回长度或波长的变化周期,它的大小取决于沉积速率的高低以及变化形式[10]。
2 旋回层序界面的识别
沉积速率是影响沉积旋回长度的一个关键参数。当沉积物供应量增加时,如果控制旋回变化的时间周期恒定,则单位时间内沉积物堆积的地层厚度大,旋回波长相应的增加;反之,当沉积速率减小时,地层沉积厚度减薄,旋回波长减小。如果在一个时间段,沉积速率是一个常量,根据沉积速率与时间长度的关系,则可将时间坐标直接转换为深度坐标。例如,当沉积速率为0.2 m/Ka时,偏心率周期、轴斜率周期、岁差周期取 400 ka、100 ka、40 ka、20 ka,这时地层序列中旋回厚度周期分别为80 m、20 m、8 m、4 m。旋回厚度周期之比为20∶5∶2∶1,这是目前在潮坪沉积或深海沉积中识别米兰科维奇周期的重要标志[11~15]。但是,地层剖面中沉积速率一般是变化的,这时采用全井段数据序列的频谱分析,频谱峰之间必然出现相互叠加和干扰,这时判读地层旋回的周期关系极为困难。为了解决这一问题,可以引进滑移窗频谱分析技术,它有助于我们直观地判断沉积速率变化的界面,进而按井深分段解析旋回层序变化周期。
为了说明沉积速率变化与米兰科维奇频带旋回记录的关系,兹以距今3 000 ka日平均辐照量为例予以说明。设定 0~500 ka、500~1 500 ka、1 500~2 000 ka、2 000~2 500 ka、2 500~3 000 ka五个时段的沉积速率分别为0.2 m/ka、0.5 m/ka、0.3 m/ka、0.8 m/ka、0.2 m/ka,将时间域数据序列转化为深度域数据序列,则在3 000 ka时间区间沉积地层累积厚度为1 250 m。对深度域时间序列进行滑移窗频谱分析,可观察到沉积旋回波长的变化特点(图2)。
观察图2可以发现,在沉积速率恒定的井段,滑移窗频谱图可检测到岁差周期的特征谱峰,但随着沉积速率的高低变化,频谱峰发生侧向迁移。在这里,旋回谱系转换界面指示沉积速率突变界面,它可能指示地层间断面,也可能是沉积体制转型界面的位置,这为我们应用频谱分析技术识别和划分旋回层序界面提供了一个重要标志。同时,采用沉积速率突变界面作为分界标志,针对层序界面之间井段区间的数据系列,分井段进行频谱分析,解释多级沉积旋回与米兰科维奇天文周期之间的关系,可以避免对频谱峰之间比例关系的错误解读。
3 研究实例
3.1 现代深海钻孔沉积速率变化界面的验证
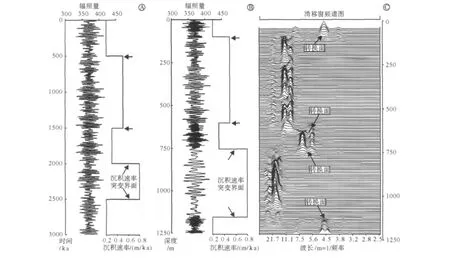
图2 沉积速率随地层深度间隔变化时日照量频谱信号的滑移窗法频谱分析Fig.2 Frequency signals of insolation data series are detected by sliding-window spectral analysis in stratigraphic intervals with sedimentation rate changes
在ODP计划开展的深海沉积研究过程中,关键一步是通过生物地层和磁性地层控制点的年代,计算沉积速率,将深度标定的气候变化指标换算为时间数据序列,进而在时间坐标上研究米兰科维奇旋回对气候变化的控制。这些深海研究工作,建立了精细的钻孔井深与年龄的对应关系,这为我们检验沉积速率转换界面,提供了最佳的实验材料。兹以深海钻孔大西洋154航次为例,采用自然伽马测井数据频谱分析方法检测沉积速率突变界面,并与地层模式年龄建立的沉积速率变化曲线进行对比验证。
大西洋ODP154航次929站位于Ceara Rise地区,我们选用929A钻孔进行研究,钻孔地理坐标坐标 5°58.573'N,43°44.396'W,海底水深4 357.5 m,钻穿深海沉积527.5 m。文章引用的测井数据和深度年龄模式下载自http://iodp.tamu.edu/网站,有关自然伽马测井方法和数据处理流程可参见King和Ellis[16]的研究报告。根据地层控制点年龄与对应的井深关系图,选取沉积速率变化幅度最大且测井数据连续的150~250 m井段进行研究,通过年龄控制点计算的沉积速率变化如图3所示。
154 航次的929A钻孔自然伽玛测井数据的单位为TC,记数时间为10s,测点间距平均为0.12 m,井深单位为 mbfs。采用 Analyseries软件的 Blackman-Tukey滑动窗频谱分析程序,首先对原始数据进行等间距线性内插和一阶导数平滑处理,选用Parzen窗口,窗口数量设定为150,最后输出文本数据进行制图。观察图3可以发现,深度150~250 m地层段可分划分五个层段,每一个层段的频谱峰的波长、强度以及谱峰个数有所不同。频谱峰转换和终止界面分别出现在深度170 m、189 m、211 m、231 m处,它是沉积速率转换界面(SRTDS)出现的标志。这4个界面出现的位置,与深度年龄模式计算的沉积速率转换点的深度一致。
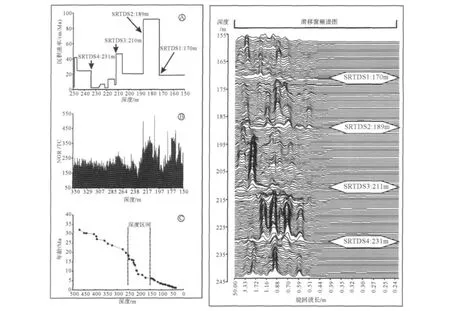
图3 根据深海154航次929钻孔自然伽马测井数据识别的沉积速率转换界面与深度—年龄模式计算沉积速率变化曲线对比图Fig.3 Correlation of abrupt change surfaces of sedimentation rates detected by spectral analysis from natural gamma data in Hole 929A at Leg 154 site(ODP)with sedimentation rate calculation curve from depth and age data
3.2 川西坳陷须家河组层序界面位置的判别
川西坳陷位于龙门山前缘地带,它是印支期形成的前陆盆地,地域范围西起龙门山推覆带,东至达县—合川—宜宾一线。川西前陆盆地以中三叠世雷口坡组海相碳酸盐岩为沉积基底,上三叠统须家河组厚度巨大,沉积中心紧靠龙门山造山带一侧,地层厚度超过4 000 m,发育巨厚的湖泊、沼泽及河流、三角洲相的煤系沉积。由于须家河组中已经发现多个油田和气田,因此其层序地层格架建立和对比受到普遍的重视。但是,目前有关须家河组层序地层界面的划分并没有取得一致意见。
例如,邹光富等[17]最早根据地表露头剖面的研究,在须家河组二段和五段划分出五个三级层序,何鲤等[18]根据地震反射界面特征将须二段至须五段划分为4个层序,刘金华等[19]则认为同一地层单元中仅存在出3个三级沉积层序。在这些沉积层序划分方案中,层序数目不一,因此每一层序持续的时间也有所差异,但有一个共同之处就是层序界面与岩石地层单元界线重叠。而在姜在兴等[20]和李熙喆等[21]的三级层序划分方案中,三级层序界面一般出现在须五段、须三段、须二段内部。为了验证须家河组层序界面的位置,我们选用川西坳陷中部的川鸭95井的测井曲线进行旋回界面检测。
根据钻井分层数据,川鸭95井钻遇的须家河组位于井深2 148~5 050 m井段,可分4段,包括须五段至须二段,下伏上三叠统海陆过渡相小塘子组,顶部为下侏罗系统白田坝组覆盖。选取井深2 100~3 000 m须五段—须四段的自然伽马进行研究。
测井数据处理流程如下:(1)采集测井曲线的高值点建立一个极值点数据序列;(2)采用线性内插法将测井极值曲线换算为等间距测点数据序列;(3)采用3点滑动平均值法过滤高频背景噪音,同时采用一阶导数法消除低频波干扰;(4)采用Analyseries软件的Blackman-Tukey滑动窗频谱分析程序,调用Parzen窗口,窗口数量150;(5)按文本格式导出数据,绘制二维频谱分布图。图5中分别标绘了原始自然伽玛测井曲线、极值点曲线、深度域滑移窗频谱分布曲线,为了说明旋回层序界面和岩石地层界线的关系,图4中还标定了须五段—须四段地层分界线的位置以及旋回层序界面的井深。
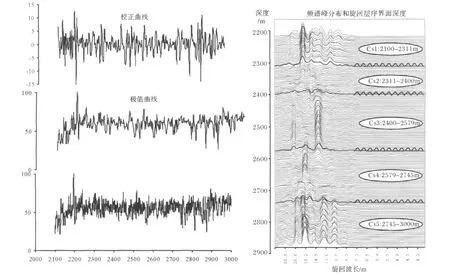
图4 川西前陆盆地川鸭95井须家河组上部自然伽马测井曲线、极值曲线和滑移窗频谱分析图Fig.4 Diagrams showing natural gamma curve,extreme point curve and sliding-window spectral analysis from extreme point data extracted from original natural gamma log in Chuanya Hole 95 of the western Sichuan foreland basin
观察图4中滑移窗频谱图中频谱峰的分布,可以发现,分析井段频谱峰的分布既有单峰型,如旋回层序Cs4所见,也有双峰式(Cs3)和多峰式(Cs1和Cs5),旋回波长变化于10~30 m之间。单峰式旋回指示一个井段存在等厚的岩性旋回,双峰、三峰和多峰式旋回反映地层中高频和低频节律共同存在。旋回波长的阶步式偏移以及频谱峰组合的变化,则是沉积速率变化或旋回层序界面出现的标志。据此,可将须家河组五段和四段划分为五个旋回层序,同时可以发现这些受沉积速率变化控制的旋回层序界面,与组段级地层单元界线可以是一致的,如Cs3与Cs4旋回层序之间的界面大致对应须五段与须四段界面,但其它层序界面与地层界线并不重合,而是位于地层单元内部。
4 讨论
在地下钻井剖面中,自然伽马测井曲线(GR)能敏感的反映泥质含量变化,而且具有数据序列连续、纵向分辨率高、等间距采样的特点,因而在旋回地层研究中得到了广泛的应用[22~25]。
在现代深海钻孔的旋回地层研究中,由于有精细的生物地层和磁性地层控制,故一般采用时间域数据序列进行频谱分析,进而探究岁差变化周期(20 ka)、黄赤交角变化周期(41 ka)、地球绕日轨道偏心率变化周期(100 ka)与地球气候变化、冰期—间冰期旋回的关系。即使在陆地剖面开展的研究,也是选用那些岩性旋回简单且沉积速率为常数或变化幅度不大的远洋沉积的地层剖面进行工作。
我们认为,无论是陆相地层还是海相地层,是碳酸盐岩沉积抑或是碎屑岩沉积,地层旋回的节律普遍存在,它可以通过测量岩性的物理参数或化学参数来度量,并可以通过频谱分析来检测,但这些旋回并不一定与气候旋回之间具有一一对应的关系。沉积旋回持续的时间长度可能受海平面、湖平面周期性波动或幕式构造旋回等诸多因素的影响,但同一类型旋回频谱谱系在深度域的变化,是沉积速率突然变化的直接表现。而沉积速率突变界面具有重要地层划分和对比意义,它通常对应地层间断面,也可能是海侵—海退旋回的转换面,或者是反映沉积环境变化的岩相界面。
原始测井数据一般测点间距为0.125 m,在频谱分析过程中可检测到高频米级旋回信号,而在极值点测井数据序列中可鉴别波长为10 m级的低频旋回周期。这二个级次旋回周期在旋回地层学研究中具有不同的含义,但根据频谱分析方法检测的高频和低频旋回信号,其形成机制和控制因素可能并不相同,旋回谱系波长的变化仅受沉积物供应速率大小的控制。沉积供应量大,沉积速率高,旋回波长增大;反之,沉积供应量减小,沉积速率降低,旋回波长减小。因此,旋回波长在深度域的变化可以作为相对沉积速率变化的指标,这是我们通过测井数据的频谱分析划分旋回层序的理论基础。但是在具体研究过程中,有以下二个问题应引起注意:
(1)数据序列中测点间距的大小,即时间分辨率的高低,对判别沉积旋回波长与米兰科维奇周期之间的关系具有明显的影响。如果没有精确的年代控制校正旋回的持续时间,仅根据偏心率和岁差之间具有20∶1和5∶1的固定比例关系来判别旋回波长对应的米兰科维奇天文周期可能出现误差,尤其是沉积速率的变化层段,在频谱分析图上会出现频谱峰的叠加,这时要判读频谱峰的关系极为困难,更甚者可能出现错误的解释。因此,在旋回地层研究中,首先应该采用滑移窗频谱分析对全井段深度数据序列进行扫描,再根据旋回层序界面的深度位置对原始测点数据进行分割,分井段进行周期图法频谱分析,最后根据每一井段检测特征频谱峰进行旋回波长的配比分析,才能取得正确的结果。
(2)在地层厚度100 m级短序列的测井数据的旋回层序分析过程中,一般通过原始测井数据的频谱分析,既可以检测到米级高频旋回的频谱峰。而对于地层厚度1 000 m级长序列测井数据,由于背景噪音的干扰,特别是在岩性复杂、测井曲线变幅大的井段,有时会出现频谱峰消失或杂乱分布的情况,这时通过提取原始测井数据的峰值曲线,则可以检测到清晰且稳定的频谱信号。同时,为了抑制低频波弥散信号对高频信号的屏蔽效应,有时必须采用一阶差分或一阶导数计算方法对峰值数据系列进行处理,才可能有效的检测地层记录中沉积旋回的频谱峰。一般根据原始测井数据的识别高频旋回界面,适用于油田开发阶段井间对比,而极值测井数据分辨的低频旋回界面,在区域地层对比方面更为有效。
5 结论
(1)通过提取测井曲线中高点峰值和低点谷值,建立极值曲线数据系列,可以分别检测低频和高频沉积旋回的波长,根据分级检测的旋回波长之间的比例关系,提取地层记录中的米兰科维奇天文信号,才能正确解释正确沉积节律与地球轨道天文周期的对应关系。
(2)沉积速率大小是控制沉积旋回波长的一个重要因素,沉积速率高,旋回波长增大,当沉积速率降低时旋回波长减小。因此,旋回波长在深度域的变化可以作为相对沉积速率变化的指标,这是我们通过测井数据的频谱分析划分旋回层序的理论基础。
(3)地层序列中沉积速率的突变界面,通常是地层间断面或沉积体制转型的位置,它具有重要的区域对比意义,根据测井数据频谱分析识别的旋回谱系波长在深度的阶步式偏移特征,可以有效地鉴别沉积速率突变面,进而标定旋回层序界面的位置。
References)
1 Schwarzacher W.Cyclostratigraphy and the Milankovitch Theory[M].Amsterdam:Elsevier,1993:1-225
2 Weedon G.Time-Series Analysis and Cyclostratigraphy:Examining Stratigraphic Records of Environmental Cycles[M].Cambridge,UK:Cambridge University Press,2003
3 陈建业,冯庆来,陈晶,等.广西东攀二叠系一三叠系界线剖面基于岩石磁参数的米兰科维奇旋回特征和地层对比[J].地层学杂志,2007,31(4):309-316[Chen Jianye,Feng Qinglai,Chen Jin,et al.Cyclostratigraphy and stratigraphic correlation based on rock magnetic parameters on the Permian-Triassic boundary in the Dongpan section in Guangxi[J].Journal of Stratigraphy,2007,31(4):309-316]
4 Gorgas T J,Wilkens R H.Sedimentation rates of SW Africa since the late Miocene deciphered from spectral analyses of borehole and GRA bulk density profiles:ODP Sites 1081-1084[J].Marine Geology,2002,180:29-47
5 Postma G,Ten Veen J H.Astronomically and tectonically linked variations in gamma-ray intensity in Late Miocene hemipelagic successions of the Eastern Mediterranean Basin[J].Sedimentary Geology,1999,128:1-12
6 Laskar J,Gastineau M,Joutel F,et al.A long term numerical solution for the insolation quantities of Earth[J].Astronomy and Astrophysics,2004,428:261-285
7 Paillard D,Labeyrie L,Yiou P.Analyseries 1.0:a Macintosh software for the analysis of geographical time-series[J].Eos Trabs.AGU,1996,77:379
8 Sierro F J,Ledesma S,Flores J A,et al.Sonic and gamma-ray astrochronology:Cycle to cycle calibration of Atlantic climatic records to Mediterranean sapropels and astronomical oscillations[J].Geology,2000,28:695-698
9 Ten Veen J H,Postma G.Astronomically forced variations in gammaray intensity:Late Miocene hemipelagic successions in the eastern Mediterranean basin as a test case[J].Geology,1996,24:15-18
10 伊海生.测井曲线旋回分析在碳酸盐岩层序地层研究中的应用[J].古地理学报,2011,13(4):456-466[Yi Haisheng.Application of well log cycle analysis in studies of sequence stratigraphy of carbonate rocks[J].Journal of Palaeogeography,2011,13(4):456-466]
11 D'Argenio B,Ferreri V,Amodio S,et al.Hierarchy of high-frequency orbital cycles in Cretaceous carbonate platform strata[J].Sedimentary Geology,1997,113:169-193
12 柳永清.旋回年代学及其应用意义——华北地台中寒武世碳酸盐岩鲕滩高频旋回的年代学研究[J].地质论评,2001,47(1):53-56[LiuYongqing.Cycloehronology of orbital cycles and its implication:a case study on the orbital forcing high-frequency cycles and cyclochronometer of mid-Cambrian oolitite carbonates in the north China platform[J].Geological Review,2001,47(1):53-56]
13 梅冥相,马永生,周洪瑞,等.雾迷山旋回层的费希尔图解及其在定义前寒武纪三级海平面变化中的应用[J].地球学报,2001,22(5):429-436[Mei Mingxiang,Ma Yongsheng,Zhou Hongrui,et al.The fischer plots of Wumishan cyclothems as records of third-order sea level changes in pre-Cambrian[J].Acta Geoscientia Sinica,2001,22(5):429-436]
14 龚一鸣,徐冉,汤中道,等.广西上泥盆统轨道旋回地层与牙形石带的数字定年[J].中国科学:D辑.2004,34(7):635-643[Gong Yiming,Xu Ruan,Tang Zhongdao,et al.The Upper Devonian orbital cyclostratigraphy and numerical dating conodont zones from Guangxi,South China[J].Science in China:Series D,2004,34(8):1235-1250]
15 Lever H.Cyclic sedimentation in the shallow marine Upper Permian Kennedy Group,Carnarvon Basin,Western Australia[J].Sedimentary Geology,2004,172:187-209
16 King T A,Ellis W G Jr.Development of a high-quality natural gamma data set from the Ceara Rise:critical groundwork for core and log data integration[C]∥Shackleton N J,Curry W B,Richter C,et al.,eds.Proc.ODP,Sci.Results,154:College Station,TX(Ocean Drilling Program),1997:117-134
17 邹光富,夏彤,楼雄英.四川广元地区上三叠统小塘子组、须家河组层序地层研究[J].沉积与特提斯地质,2003,23(3):73-80[Zou Guangfu,Xia Tong,Lou Xiongying.Sequence stratigraphy of the Late Triassic strata in the Guangyuan region,Sichuan[J].Sedimentary Geology and Tethyan Geology,2003,23(3):73-80]
18 何鲤,段勇,罗潇,等.川西坳陷上三叠统层序地层划分新方案[J].天然气工业,2007,27(2):6-11[He Li,Duan Yong,Luo Xiao,et al.New scheme of sequence stratigraphic division for Upper Triassic in western Sichuan depression[J].Natural Gas Industry,2007,27(2):6-11]
19 刘金华,张世奇,孙耀庭,等.川西前陆盆地上三叠统须家河组地层的划分对比及沉积演化[J].地层学杂志,2007,31(2):190-196[Liu Jinhua,Zhang Shiqi,Sun Yaoting,et al.Correlation and evolution of the Upper Triassic Xujiahe Formation in the west Sichuan foreland basin[J].Journal of Stratigraphy,2007,31(2):190-196]
20 姜在兴,田继军,陈桂菊,等.川西前陆盆地上三叠统沉积特征[J].古地理学报,2007,9(2):143-154[Jiang Zaixing,Tian Ji-jun,Chen Guiju,et al.Sedimentary characteristics of the Upper Triassic in western Sichuan foreland basin[J].Journal of Palaeogeography,2007,9(2):143-154]
21 李熙喆,张满郎,谢武仁,等.川西南地区上三叠统须家河组沉积相特征[J].天然气工业,2008,28(2):54-57[Li Xizhe,Zhang Manglang,Xie Wuren,et al.Sedimentary facies of Upper Triassic Xujiahe Formation in southwest Sichuan Basin[J].Natural Gas Industry,2008,28(2):54-57]
22 张小会,赵重远.鄂尔多斯盆地上三叠统延长组米兰科维奇旋回的确定[J].石油与天然气地质,2002,23(4):372-375[Zhang Xiaohui, Zhao Zhongyua.Definition of Milankovitch cycles for Yangchang Formation of the upper Triassic in Ordos Basin[J].Oil and Gas Geology,2002,23(4):372-375]
23 郑兴平,罗平.川东渝北飞仙关组的米兰克维奇周期及其应用[J].天然气勘探与开发,2004,27(1):16-19[Zheng Xingping,Luo Ping.Analysis and application of Milankovitch cycles on Feixianguan Formation,northeast Sichuan Basin,China[J].Gas Exploration and Development,2004,27(1):16-19]
24 李凤杰,王多云,程微.应用自然伽马曲线反演陇东地区延安组沉积旋回[J].成都理工大学学报:自然科学版,2004,31(5):473-477[Li Fengjie,Wang Duoyun,Cheng Wei.Use of natural gamma-ray well log to study sedimentary cycles of Yan'an Formation in Eastern Gansu,Ordos Basin,China[J].Journal of Chengdu University of Technology:Science& Technology Edition,2004,31(5):473-477]
25 李斌,孟自芳,李相博,等.靖安油田延长组米兰柯维奇沉积旋回分析[J].地质科技情报,2005,24(2):64-70[Li Bin,Meng Zifang,Li Xiangbo,et al.Analysis of Milankovitch cycles of Yanchang Formation in Jing’an Oilfield[J].Geological Science and Technology Information,2005,24(2):64-70]
