二阶电路的动态响应分析与仿真
2012-11-13冯巧红
冯巧红,郑 微
(1.滁州职业技术学院机电系,安徽 滁州 239000;2.长丰县杨庙镇中心学校,安徽 长丰 231100)
二阶电路的动态响应分析与仿真
冯巧红1,郑 微2
(1.滁州职业技术学院机电系,安徽 滁州 239000;2.长丰县杨庙镇中心学校,安徽 长丰 231100)
二阶电路的动态分析与研究无论在研究领域或是实际工程应用上都有较为重要的意义。文章给出了二阶电路的一般分析方法,讨论了二阶电路直接进入稳态的条件,并利用MATLAB进行动态仿真,验证了分析的正确性。
二阶电路;暂态分析;MATLAB;过渡过程;响应
当电路中含有储能元件(如电容、电感)且电路的结构或元件参数发生改变时,电路的工作状态将由原来的稳定状态转变为另一个稳定状态。由于能量是不能突变的,所以这种转变一般来说不是即时完成的,需要经历一个过程,这个过程被称作动态过程或过渡过程,简称暂态。电路的暂态虽然短暂,但是在暂态时间内,电路会出现数值上为额定值的几十倍、甚至上百倍的过电压或过电流。这些过电压或过电流在电力系统中具有较严重的危害性,它容易造成电路组件的击穿、电气设备的绝缘损坏等,严重时可以造成电气事故。所以在供电系统中需要严加控制,避免出现严重的后果。然而,在电子技术中,我们往往利用电路的过渡过程来改善或产生一些特定的波形。因此,对电路的过渡过程的分析具有重要的意义。下面我们针对二阶电路的暂态过程进行分析研究,这个分析方法具有一般性,可为二阶电路甚至多阶电路的研究提供参考。
1 二阶电路的动态分析
1.1 二阶电路的数学模型
图1电路中含有两个储能元件,设电路初始条件uc(0-)=U0,在t=0时开关S闭合,根据基尔霍夫电压定律(KVL)可得:

可见该电路与动力学中单自由度有阻尼振动系统具有相同的数学模型。此方程为二阶常系数非齐次微分方程。在复频域内求解,对等式两边进行拉氏变换得

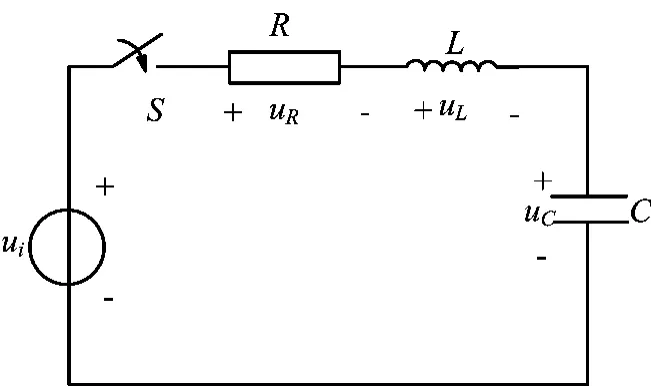
图1

1.3 电路的零状态响应
当电路的输入信号ui不同时,输入电路的零状态响应U2(S)具有不同的形式为了具有一般性,这里选用正弦交流信号作为电路的输入信号,设ui=Umsin(ωt+φ0)其拉氏变换为

1.4 电路的全响应
根据上述分析可得电路的全响应为
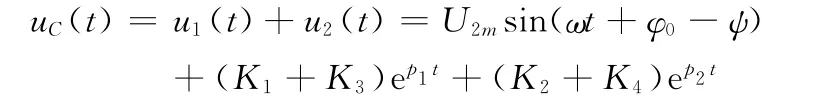
可见电路的全响应分为两部分组成:
U2msin(ωt+φ0-ψ)为电路的稳态响应;(K1+K3)ep1t+(K2+K4)ep2t为电路的暂态响应,也就是电路的过渡过程。
2 电路直接进入稳态的条件
正常情况下含有储能元件的电路在换路时,由于能量不能突变,故都要经历一个暂态也即过渡过程,由上面分析的二阶电路在正弦激励下的全响应可见,要使电路不经历暂态而直接进入稳态得条件就是:
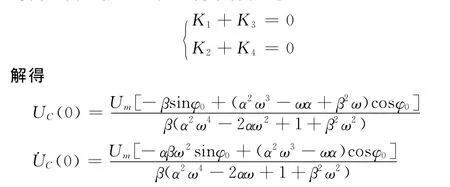
可见当UC(0)、˙UC(0)、φ0三者之间满足一定关系时,电路可以不经历过渡过程(暂态)而直接进入稳定
状态。
3 基于MATLAB下二阶电路的动态分析和仿真
3.1 一般情况下动态仿真
考虑在一般情况下忽略初始条件之间的关系取R=0.5Ω,L=0.25H,UC(0)=2V,C=0.5F,ui= 110sin31.416tV,˙UC(0)=0时,在MATLAB下得到uc(t)的响应波形如图2所示。
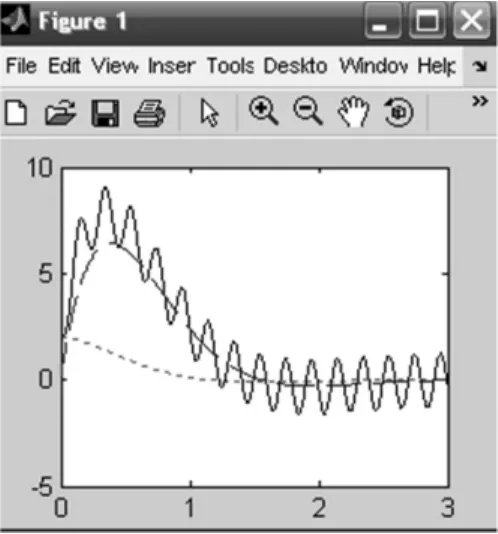
图2
可见电路在换路后较短时间内出现了远远高于稳态电压的过电压,经过一段时间后进入稳态。
3.2 电路直接进入稳态的仿真
根据上面讨论的当三者之间满足一定的关系时,电路可以直接进入稳态,当电路结构参数同上并且设定˙UC(0)=0,UC(0)=-1.2587V,ui= 110sin(31.416t+1.4431)也即初始条件满足上述分析中电路直接进入稳态的条件时,则得电路的动态响应如图3所示。可见电路虽存在零输入响应和零状态响应两种不同的暂态响应,但是由于初始条件和激励的状态配置,使得零输入和零状态响应的暂态正好相互抵消,从而使得电路的全响应是直接进入稳态并不存在过电压、过电流现象,也即电路没有过渡过程或是暂态响应。
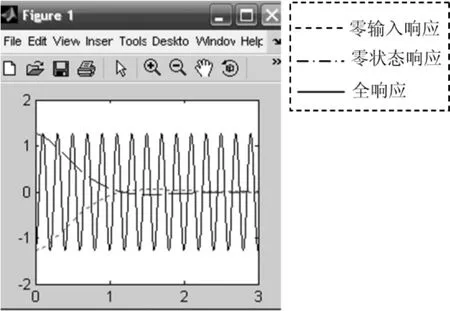
图3
4 结束语
综上所述,二阶电路在换路后一般情况都要经历暂态响应,在暂态响应中会出现过电压、过电流现象。电路的暂态响应与电路本身的结构参数、电路换路时的初始状态以及外部激励有关。在电路的结构参数一定的前提下,电路的暂态响应不仅与电路的初始状态有关,还与换路瞬间(t=0)时外部激励的状态有关,也即与换路时刻有关,不同的换路时刻会出现不同的暂态响应。也就是说,当电路的结构参数一定时,如果电路的初始状态和换路时刻外部激励之间同时满足一定的关系(如上分析),就可使得二阶电路不经过过渡过程而直接进入稳态。这一重要结论对工程应用具有重要的理论和实际意义。
[1]汪金山.正弦激励下RLC串联二阶电路暂态过程的研究[J].哈尔滨理工大学学报,1999,4(1):93-96.
[2]邱关源.电路.第4版[M].北京.高等教育出版社,1999.
[3]黄忠霖.自动控制原理的 MATLAB实现[M].北京.国防工业出版社,2007.
[4]李国勇.谢克明.杨丽娟.计算机仿真技术与CAD[M].北京.电子工业出版社,2008.
[5]石 生.电路基本分析.第3版[M].北京.高等教育出版社,2008.
Analysis and Simulation to the Dynamic Response of Second Order Circuit
Feng Qiaohong,Zheng Wei
Analysis and research on the dynamic process of second-order circuit are very important both in the field of study and practical applications of engineering.On the basis of the previous studies,this article gives a general research method of second-order circuit.The conditions for the circuit directly into the steady-state are discussed and the dynamic response is simulated on MATLAB.The correctness of the analysis is verified.
second-order circuit;transient analysis;MATLAB;transition process;resp onse
TM13
A
1673-1794(2012)02-0042-03
冯巧红(1974-),女,安徽天长人,工学硕士,讲师,研究方向:自动控制。
2011-11-10
