分数-跳扩散模型下的两种奇异期权定价
2012-11-13桑利恒杜雪樵
桑利恒,杜雪樵
(1.滁州学院 数学学院,安徽 滁州 239000;2.合肥工业大学 数学学院,安徽 合肥 230009)
分数-跳扩散模型下的两种奇异期权定价
桑利恒1,杜雪樵2
(1.滁州学院 数学学院,安徽 滁州 239000;2.合肥工业大学 数学学院,安徽 合肥 230009)
在股票价格遵循带有非时齐Poisson跳跃的分数扩散过程的假定下,刻画了股票价格的相依性和市场中重大信息的到达引起股票价格的跳跃,同时利用鞅方法,导出了两种奇异期权的定价公式.
分数-跳扩散 风险中性测度 上限型买权 抵付型买权
期权是金融衍生产品中重要产品之一,而期权定价是金融数学研究的核心问题。1973年Black和Scholes提出了著名的B-S期权定价模型[1],该模型假设股票价格服从几何布朗运动。由于实际分析发现股票价格变化并不总是连续的,于是在1976年Merton首先提出了股票价格的跳过程为Poisson跳的跳扩散模型[2],其后,Aase建立了It过程和随机点过程混合模型[3];Jarrow(1992)建立了随机利率模型;Schweizer建立了一般半鞅模型[4];以及Chan建立了几何Levy过程的模型[5]等。但由于投资者的投机心理和从众心理,使得股票价格对过去价格具有某种依赖性,而分数布朗运动恰好能刻画这种依赖性,于是一些学者考虑用分数布朗运动来刻画股票价格的变化,其中贡献最为突出的是Hu和Kendal[7],他们给出了分数布朗运动随机积分的理论及其在金融中的应用。文献[8]~[11]分别研究了在分数布朗运动环境下期权定价问题。
利用分数布朗运动刻画了股票价格的变化,并且利用了Poisson过程刻画了重大信息到达时股票价格的较大波动。在此基础上假设股票价格满足分数一跳扩散过程,并设有股票预期收益率,波动率和无风险利率均为时间函数。运用鞅方法给出了上限型实权和抵付型买权两种奇异期权的定价公式。
1 预备知识与模型假设
定义1.1[7]设0<H<1,Hurst参数为 H的分数布朗运动为一个连续高斯过程{BH(t),t∈R+},满足BH(0)=0和E[BH(t)]=0且协方差为:

设(Ω,F,Ft,P)是一个具有σ-流的概率空间,其中Ft是分数布朗运动BH(t)产生的自然σ-流。现在我们假设,Itó型分数Black-Scholes市场仅有两种证券:一种是无风险资产,假定为债券,另一种是风险资产,假定为股票,其中无风险资产的价格满足如下方程:

其中,r(t)为无风险利率。
假设风险资产的价格过程{S(t),t≥0}满足其中u(t)为股票的瞬时期望收益率,σ(t)为股票的瞬时波动率,N(t)表示股票价格在[0,t]内随机跳跃次数,它是与BH(t)独立的参数为λ(t)的非时齐Poisson跳跃过程,(Vi)i≥0表示在随机时刻i=0,1,2,…,N(t)的跳跃高度,无发生跳跃时V0=0,Vi(>-1)为股票价格发生跳跃时股票价格的相对跳跃高度,设(Vi)i≥0,N(t)与BH(t)相互独立,θ为Vi的无条件期望,即Ε(Vi)=θ,它表示股票价格由跳带来的平均增长率。记σ20为ln(1+Vi)的方差,则
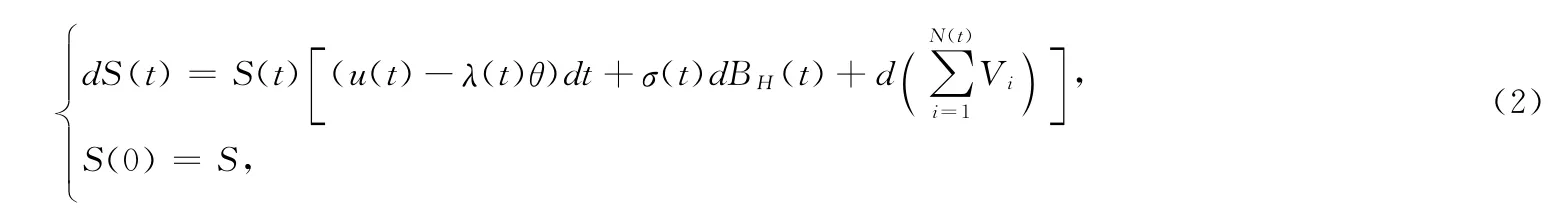

2 分数-跳扩散过程模型下的两种奇异期权的定价
2.1 上限型买权定价
定义2.1 上限型买权在到期时T的现金流量为:


证毕。
2.2 抵付型买权定价
定义2.2 抵付型买权在到期时T的现金流量为:
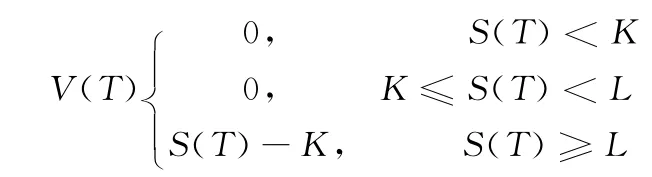
其中K<L给定,K为敲定价格,由现金流量知这种期权只有当标的资产价格S(T)高于L时才支付现金。
运用类似的证明方法可以得到以下定理:
定理2.2 设S(t),P(t)分别满足(1)和(2),则抵付型买权的定价公式为:
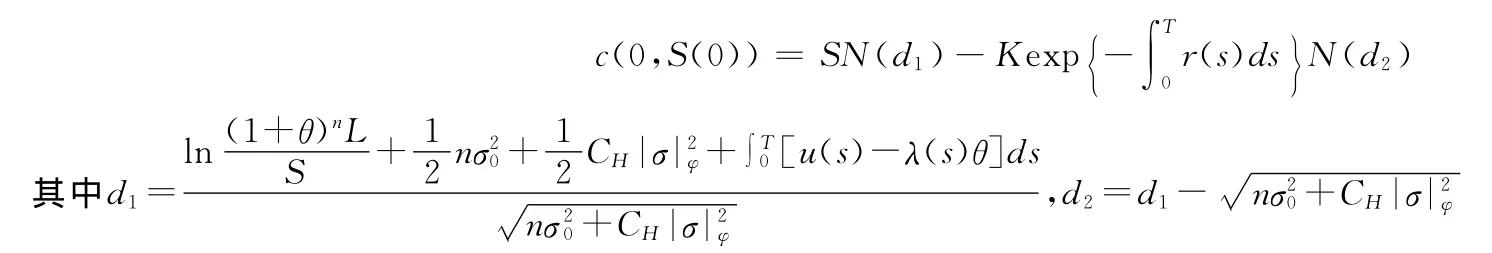
注:1)在文中所述的这两种奇异期权,当上限型权证中K2→∞,抵付型买权K=L时,则它们为欧式看涨期权。
2)当λ为常数时,方程(2)为带时齐Poisson跳跃过程的分数型扩散过程,同样可得出与上述两个定理类似的结果。
3)把假设中的0时刻该为t时刻,那么对于方程(3)则有:对于0≤t≤T有,
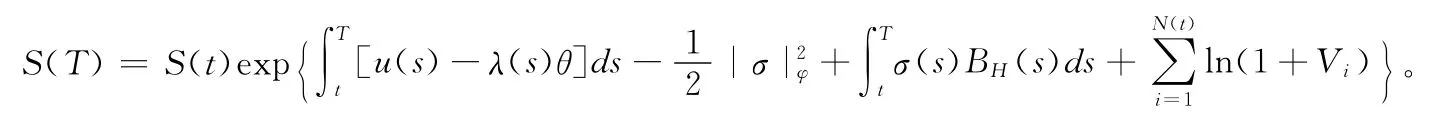
用类似的方法可以得出这两种奇异期权在t时刻的价格。
[1]Black F.Scholes M.The pricing of options and corporate liabilities[J].Journal of Political Economy,1973.81(3):637-654.
[2]Merton R C.Option pricing when underling stock returns are discontinuous[J].Journal of Economy,1976.3:125-144.
[3]Knut K,Aase.Contingent claims valuation when the security price is combination of an Itóprocess and a random point process[J].Stochastic processes and their Applications,1998,28(2):185-220.
[4]Martin Schweizer.Option heading for semi-martingales[J].Stochastic processes and their Applications,1991,37(3):339-360.
[5]Chan T.Pricing contingent claims on stocks driven by Levy processes[J].Annals of Appl Prob,1999,9(2):504-528.
[6]宁丽娟.刘新平.股票价格服从跳-扩散过程的期权定价模型[J].陕西师范大学学报:自然科学版,2003,31(4):16-19.
[7]HU Y.KENDALB.Fractional white noise calculus and applications to finance[J].Infinite Dim Anal Quantum Prob Related Topics,2003(6):1-32.
[8]Necula C.Option Pricing in a Fractional Brownian Motion Environment[R/OL].Preprint,Academy of Economic Studies Bucharest.Romania,2002.www.dofin.ase.ro.
[9]刘韶跃,杨向群.分数布朗运动环境中欧式未定权益定价[J].应用概率统计,2004,20(4):429-434.
[10]张学莲,薛 红.股票价格遵循分数一跳扩散过程的期权定价[J].纺织高校基础科学学报,2008,21(4):446-450.
[11]梅正阳,杨玉孔.基于鞅方法的分数Brown运动模型的期权定价[J].应用数学,2008,21(4):727-730.
[12]Merton Robert C.Continuous-Time Finance(Revised Edition),Blackwell Publishers Inc.,(1997).中文版.R.C.默顿,连续时间金融(修订版),北京:中国人民大学出版社,(2005).
Pricing of Two Kinds of Exotic Options with a Fractional-Jump-diffusion Models
Sang Liheng,Du Xueqiao
In order to characterize the dependence in stock prices and the stock price jumps caused by the arrival of significant information in markets,this article assumes the stock price follows with a nonhomogeneous Poisson jump-diffusion process scores and derives the pricing formulas of the two exotic options by martingale method by the way of the existing integral theory.
Fractional-Jump-diffusion;risk-neutral measure;capped calls;deductible calls
0211.6
A
1673-1794(2012)02-0028-04
桑利恒(1983-),男,安徽太和人,助教,理学硕士,研究方向:金融工程。
滁州学院校级科研项目(2011KJ003B)
2011-12-22
