投影矩阵在单形体积公式中的应用
2012-11-13殷红彩张华民
殷红彩,张华民
(安徽财经大学 管理科学与工程学院,安徽 蚌埠 233000;蚌埠学院 数理系,蚌埠 233030)
投影矩阵在单形体积公式中的应用
殷红彩1,张华民2
(安徽财经大学 管理科学与工程学院,安徽 蚌埠 233000;蚌埠学院 数理系,蚌埠 233030)
利用投影矩阵和正交投影矩阵讨论了单形的多维角,建立了多维角正余弦的表达式,由此得到了单形的一类体积公式,并给出了投影矩阵的性质和第二高维余弦定理的一种新证法.
投影矩阵;正交投影矩阵;单形体积公式
近期有文献讨论了单形的多维角及相应的体积公式,以及对单纯形的正弦定理和余定理给出了新的证法。例如文献[1]讨论了单纯形的正弦定理,给出了一个体积公式,文献[2]给出了单形高维余弦定理和正弦定理的新的证法,文献[3]依据多维角对单形的体积公式进行了整理分类,文献[4]对文献[1]建立的单形的体积公式进行了更为一般的推广,即建立了一个新的单形体积公式,文献[5]建立了单形内二面角及外二面角角平分面的两个性质定理。在上述文献中对相关定理和公式的证明多采用凸体几何的方法或初等的方法,以投影矩阵和正交投影矩阵为手段建立单形的体积公式并不多见,本文尝试用矩阵为手段对上述的内容进行讨论。第一部分讨论最简单的两个向量所成的角,第二部分讨论一个和多个向量成的的角,第三部分讨论多个向量间所成的角,最后一部分对所得的结果给出一些评论。
1 两个向量所成的角及应用

其中内积定义为〈p1,p2〉=pT1·p2,即单个的向量p1也表示它对应的n维列向量.本文主要讨论在单形体积公式中的应用,故角度余弦均取非负值.
分子为这两个向量的内积,分母为这两个向量的长度.上面三角形面积公式中用到了角的正弦,而(2)式给的是余弦,下面来建立角θ(p1,p2)的正弦,设向量p2的投影矩阵和正交投影矩阵分别为
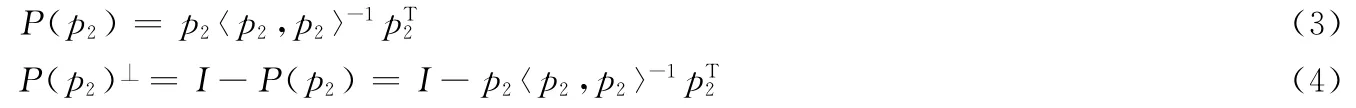
可求得向量p1在向量p2方向上的投影向量为P(p2)p1=p2〈p2,p2〉-1pT2p1,在p2的正交补(或垂直)方向上的正交投影向量为
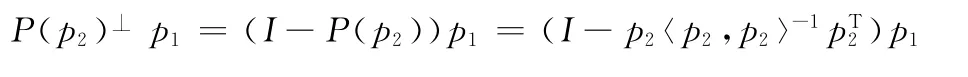
受sinθ=的启发,给出下面的定义.定义1 设p,p为n维欧氏空间中的两个n维向量,所成的角记为θ(p,p)其中0≤θ(p,p)≤,则θ(p,p)的
12121212
正弦,余弦分别定义如下

其中P(p2),P(p2)⊥分别表示向量p2的投影矩阵和正交投影矩阵.
下面说明公式(2)与公式(6)是一致的.
定理1 相关符号如上文所述,则有下面等式成立
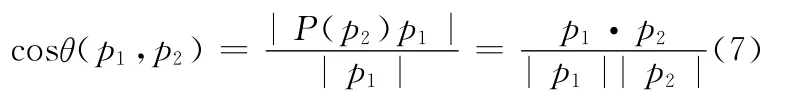
证明 证明等式左边等于右边,
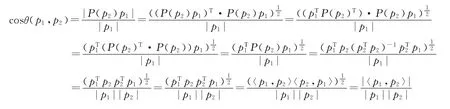
定理得证.
上述证明中用到了投影矩阵的对称性和幂等性,由此可得n维欧氏空间中三角形的面积公式
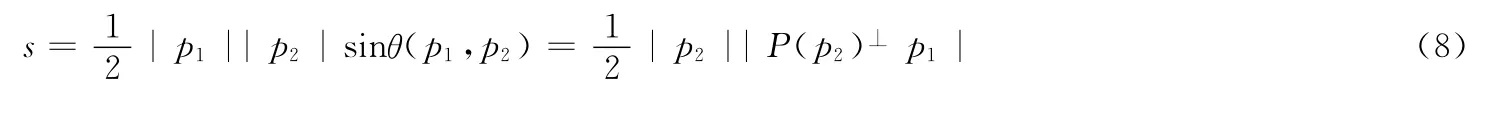
2 一个向量与多个向量成的角及应用
下面给出在n维欧氏空间中一个n维向量与多个n维向量所成的角及应用,记p1,p2,…,pk是k(2≤k≤n)个n维向量,记A=[p2,…,pk],A∈Rn×(k-1),则A的投影矩阵与正交投影矩阵分别为
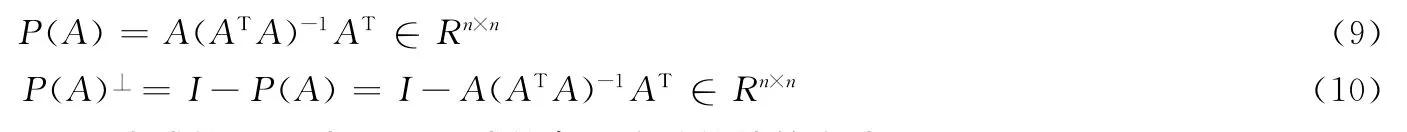
由此可得向量p1与向量组p2,…,pk生成的k-1超平面所成的角正余弦的计算方法,
定义2 向量p1与向量组p2,…,pk生成的k-1超平面所成的角记为θ(p1,A),其中A=[p2,…,pk]∈Rn×(k-1),则角θ(p1,A)的正余弦分别定义为

据此可得,k维超平行体(或单形)的体积公式.
定理2 由向量p1,p2,…,pk生成的超平行体有下面的体积公式
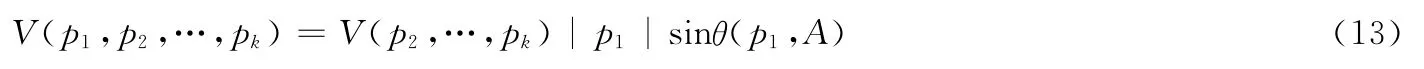
其中V(p1,p2,…,pk)表示由向量p1,p2,…,pk生成的超平行体的体积.
证明 为了表述方便,证明(13)式两边平方相等,右边平方等于左边,证明如下
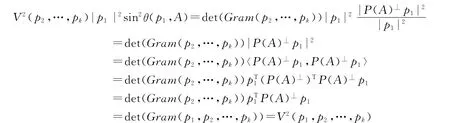
右边等于边,证毕.
上述det(Gram(p1,p2,…,pk))表示向量p1,p2,…,pk的Gram矩阵的行列式.若记
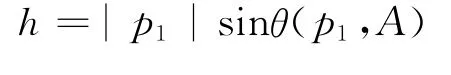
则(13)式就是文献[6]中的一个公式.
3 多个向量间成的角及应用
下面考虑多个向量间所成的角及应用.
在n维欧氏空间中n个线性无关的n维向量p1,p2,…,pn生成超平行体,考虑向量组p1,p2,…,pk(k≤n-1)生成的超平面与向量组p2,…,pn生成的超平面所成的角,记A=[p2,…,pk],B=[p2,…,pn],矩阵A,B的投影矩阵与正交投影矩阵分别记为P(A),P(B),P(A)⊥,P(B)⊥,P(A),P(A)⊥的定义同(9)与(10)式,而P(B),P(B)⊥的定义如 下:
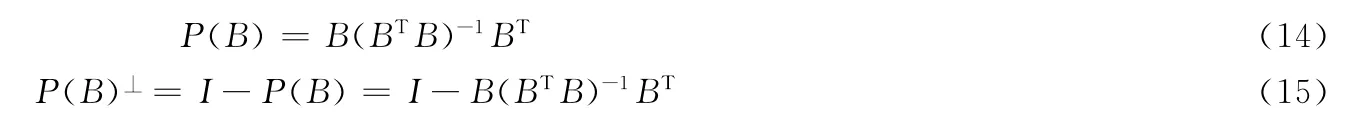
定义3 设向量组p1,p2,…,pk与向量组生成的超平面所成的角记为θ(A,B),若记α=P(A)⊥p1,β=P(B)⊥p1,则角θ(A,B)的正余弦定义如下

左右两边相等,结论成立.
很明显在(15)中|α|,|β|分别相当于直角三角形的斜边和一条直角边,此即文献[4]中的主要结论.但在文献[4]中只给出了角θ(A,B)的正弦的定义,并未给出余弦的定义,下面说明定义(16)式的合理性.即有结下面的结论:
定理4 sin2θ(A,B)+cos2θ(A,B)=1
证明


注意到p1的取值范围,即得P(B)⊥=P(A)⊥P(B)⊥.
将P(B)⊥=P(A)⊥P(B)⊥变形即得
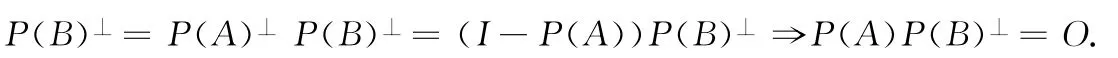
再将P(A)P(B)⊥=O变形为P(A)(I-P(B))=O,即得P(A)=P(A)P(B).证毕.
据定理4可得几个关于投影矩阵和正交投影矩阵的结论:
定理5 设向量组p2,…,pk与p2,…,pn分别是两个线性无关的n维向量组且集合{p2,…,pk}⊆{p2,…,pn},记它们构成的矩阵为A=[p2,…,pk],B=[p2,…,pn],记它们的投影矩阵与正交投影矩阵分别为P(A),P(B),P(A)⊥,P(B)⊥,则有下面结论

其中O表示零矩阵.
最后,应用公式(17)给出第二高维余弦定理的一种新证明.若n维单形由n个线性无关的n维向量p1,p2,…,pn生成,考查两个超平面所成角的余弦,在文献[2][7]中有第二高维余弦定理:
第二高维余弦定理n维欧氏空间中由向量组p1,p2,…,pn生成的n维单形,记由向量组p1,p2,…,pn-1与p2,…,pn生成单形的两个侧面所成的内二面角记为θ1n,则它的余弦为其中Pij表示向量组p1,p2,…,pn的Gram矩阵行列式P中元表的代数余子式.
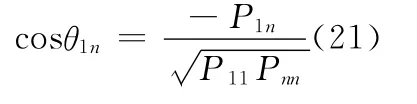
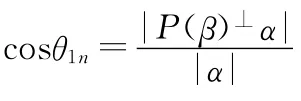

4 结束语
从证明过程可以看出,借助矩阵的手段整个过程显的更有条理性,知识的展开更有系统,比起文献[1-4]中体积公式的获得更显自然,当然我们也可以用矩阵的方法来建立文献[5]中的结果,由于篇幅有限作者另文表述。
[1]ERIKSSON F.The law of sines for tetrahedra and nsimplices[J].Gemo Dedicata,1978,7:71-80.
[2]张华民,殷红彩,杨世国.中 维余弦定理和正弦定理的新证[J].数学的实践与认识,2009,10:249-252.
[3]张华民,杨世国.单形的一类体积公式[J].合肥工业大学学报(自然科学版),2008,3:489-492.
[4]张华民,杨世国.一个新的单形体积公式[J].浙江大学学报(理学版),2008,1:5-70.
[5]殷红彩,张华民.单形二面角角平分面的性质[J].浙江大学学报(理学版),2012,2:46-50.
[6]沈文选.单形论导引[M].长沙:湖南师范大学出版社,2000,70.
[7]杨 路,张景中.关于有限点集的一类几何不等式[J].数学学报,1980(5)740-749.
[8]张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004,670.
Applications of Projection Matrix to a Simplex Volume Formula
Yin Hongcai, Zhang Huamin
By using the projection matrix and the orthogonal projection matrix,the multi-dimension angle of a simplex is discussed and the expression of sine and cosine is acquired.At the same time we get a kind of volume formula for a simplex and a new way to prove the second high dimension cosine law.
simplex;projection matrix;orthogonal projection matrix;volume formula for a simplex.
O184
A
1673-1794(2012)02-0024-04
殷红彩(1981-),女,安徽砀山人,硕士研究生,安徽财经大学教师,研究方向:矩阵理论。
蚌埠学院自然科学项目(2011ZR17)
2012-02-05
